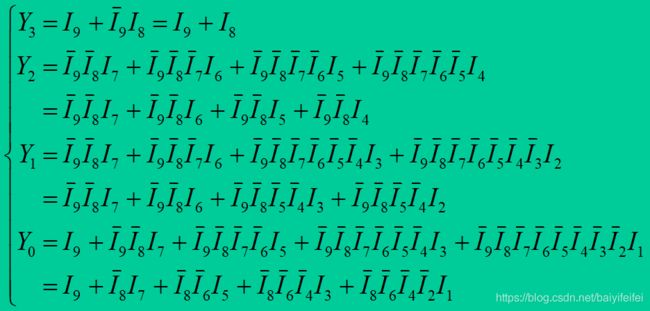数字电子技术复习
Chapter 1 逻辑代数基础
知识点纲要
- 掌握逻辑代数的三种基本运算、五种复合运算(逻辑定义、表达 式、真值表、逻辑符号、混合逻辑)
- 掌握逻辑代数的公式、定理和规则
- 掌握逻辑函数的几种表示方法及其相互转换,包括真值表、逻辑表达 式、逻辑图、最小项表达式、卡诺图
- 熟练掌握逻辑函数的两种化简方法(代数法、卡诺图法)
- 掌握用与非门、或非门、与或非门实现逻辑函数的方法
Point 1
逻辑代数的三种基本运算
- 与运算
逻辑定义:只有决定事物结果的全部条件同时具备的时候,结果才发生
表达式: Y = a ⋅ b Y=a\cdot b Y=a⋅b
真值表:
| A | B | Y |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
逻辑符号:‘ ⋅ \cdot ⋅’
- 或运算
逻辑定义:在决定事物结果的诸多条件中只要满足一个,结果就会发生
表达式: Y = A + B Y=A+B Y=A+B
真值表:
| A | B | Y |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
逻辑符号:’ + + +’
- 非运算
逻辑定义:只要条件具备了,结果便不会发生,而结果不具备,结果一定发生
表达式: Y = A ‾ Y=\overline{A} Y=A
真值表:
| A | Y |
|---|---|
| 0 | 1 |
| 1 | 0 |
逻辑符号:‘ − - −’
五种复合逻辑运算
- 与非
表达式: Y = a ⋅ b ‾ Y=\overline{a\cdot b} Y=a⋅b
真值表:
| A | B | Y |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
逻辑符号:‘ ⋅ ‾ \overline{\cdot} ⋅’
- 或非
表达式: Y = A + B ‾ Y=\overline{A+B} Y=A+B
真值表:
| A | B | Y |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 0 |
逻辑符号:‘ + ‾ \overline{+} +’
- 与或非
表达式: Y = A ⋅ B + C ⋅ D ‾ Y=\overline{A\cdot B+C\cdot D} Y=A⋅B+C⋅D
真值表:略 - 异或
表达式: Y = A ⨁ B Y=A\bigoplus B Y=A⨁B
真值表:
| A | B | Y |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
- 同或
表达式: Y = A ⨀ B Y=A\bigodot B Y=A⨀B
真值表:
| A | B | Y |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Point 2
重要公式
分配律: A + B ⋅ C = ( A + B ) ⋅ ( A + C ) A+B\cdot C=(A+B)\cdot (A+C) A+B⋅C=(A+B)⋅(A+C)
反演律: A ⋅ B ‾ = A ‾ + B ‾ , A + B ‾ = A ‾ ⋅ B ‾ \overline{A\cdot B}=\overline{A}+\overline{B},\overline{A+B}=\overline{A}\cdot\overline{B} A⋅B=A+B,A+B=A⋅B
常用公式:
A + A ⋅ B = A , A ⋅ ( A + B ) = A A+A\cdot B=A ,A\cdot (A+B)=A A+A⋅B=A,A⋅(A+B)=A
A + A ‾ B = A + B A+\overline{A}B=A+B A+AB=A+B
A ⋅ B + A ‾ ⋅ C + B ⋅ C = A ⋅ B + A ‾ ⋅ C A\cdot B+\overline{A}\cdot C+B\cdot C=A\cdot B+\overline{A}\cdot C A⋅B+A⋅C+B⋅C=A⋅B+A⋅C
基本定理
带入定理:在任一含有某个变量的等式中,若用另一个逻辑式代入式中所有变量的这个位置,等式仍然成立
反演定律:对任意一个逻辑式Y,若将其中所有的‘.’换成‘+’,‘+’换成‘.’,0换成1,1换成0,原变量换成反变量,反变量换成原变量,则得到的结果换成 Y ‾ \overline{Y} Y
对偶定律:若两逻辑式相等,则其对偶式(即对一个式子进行反演),也相等
Point 3
- 真值表
- 逻辑函数式
- 逻辑图
- 卡诺图
Chapter 2 门电路
知识点纲要
- 了解TTL门电路(反相器)的电路结构、工作原理及有关特性(输入特性、输出特性、电压传输特性、输入负载特性)和参数(UOH、UOL、UTH、IIS、IIH)
- 了解CMOS门电路(反相器)的电路结构、工作原理及有关特性(输入特性、输出特性、电压传输特性、输入负载特性)和参数(UOH、UOL、UTH、IIS、IIH)
- 掌握几种特殊结构的门电路的电路结构、工作原理及其应用(OC门、TSL门、TG门、模拟开关)
Point 1
TTL门电路
输入负载特性:
- 输入端短地相当于接低电平
- 输入端电阻小于1K相当于接低电平
- 输入端电阻大于1K相当于接高电平
- 输入端悬空相当于接高电平
芯片举例:7400与非门
Point 2
CMOS门电路
芯片举例:CC4016双向模拟开关
Point 3
特殊门电路
集电极开路门(OC门):可以用于实现线与

L = L 1 ⋅ L 2 = A B ‾ ⋅ C D ‾ L=L_1\cdot L_2=\overline{AB}\cdot \overline{CD} L=L1⋅L2=AB⋅CD
三态门(TS门):
- 组成单向总线,实现信号的分时单向传送;
- 组成双向总线,实现信号的分时双向传送
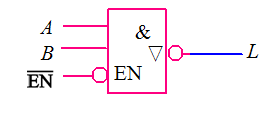
{ L = A ⋅ B ‾ E N ‾ = 0 高 阻 态 E N ‾ = 1 \begin{cases}L=\overline{A\cdot B}&\overline{EN}=0\\高阻态&\overline{EN}=1\end{cases} {L=A⋅B高阻态EN=0EN=1
传输门(TG门):电压控制电压传输

{ V o = V i C = 1 高 阻 态 C = 0 \begin{cases}V_o=V_i&C=1\\高阻态&C=0\end{cases} {Vo=Vi高阻态C=1C=0
模拟开关(SW门):

{ V o = V i C = 1 高 阻 态 C = 0 \begin{cases}V_o=V_i&C=1\\高阻态&C=0\end{cases} {Vo=Vi高阻态C=1C=0
Chapter 3 组合逻辑电路
知识点纲要
- 正确理解各种常用组合逻辑电路的逻辑功能,包括编码器、译码器、数据选择器、加法器、大小比较器、奇偶校验器
- 掌握几块集成中规模组合逻辑电路的逻辑功能及应用(74LS138、74LS283、74LS153 、74LS151、74LS148、74LS85)
Point 1 数据选择器(74LS153,74LS151)
四选一数据选择器(74LS153)

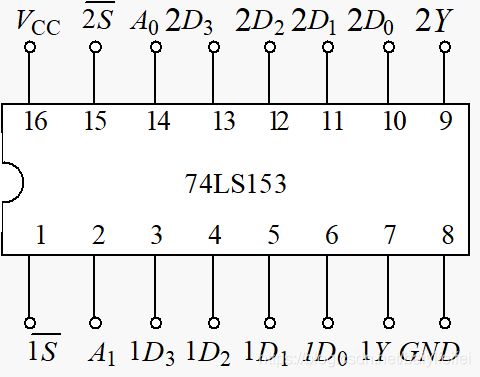
逻辑函数值:
Y = S ‾ ‾ ( A 1 ‾ A 0 ‾ D 0 + A 1 ‾ A 0 D 1 + A 1 A 0 ‾ D 2 + A 1 A 0 D 3 ) Y=\overline{\overline{S}}(\overline{A_1} \overline{A_0}D_0+\overline{A_1}{A_0}D_1+A_1\overline{A_0}D_2+A_1A_0D_3) Y=S(A1A0D0+A1A0D1+A1A0D2+A1A0D3)
真值表:
| $ \overline S$ | D | A 1 A_1 A1 | A 0 A_0 A0 | Y |
|---|---|---|---|---|
| 1 | × \times × | × \times × | × \times × | 0 |
| 0 | D 0 D_0 D0 | 0 | 0 | D 0 D_0 D0 |
| 0 | D 1 D_1 D1 | 0 | 1 | D 1 D_1 D1 |
| 0 | D 2 D_2 D2 | 1 | 0 | D 2 D_2 D2 |
| 0 | D 3 D_3 D3 | 1 | 1 | D 3 D_3 D3 |
八选一数据选择器(74LS151)


逻辑函数:
Y = { 0 S = = 1 ∑ i = 0 7 D i m i S = = 0 Y=\begin{cases}0&S==1\\\sum_{i=0}^{7}D_im_i&S==0\end{cases} Y={0∑i=07DimiS==1S==0
真值表:

Point 2编码器
三位二进制优先编码器(74LS148)

逻辑函数:

真值表:
![]()
其中: S T ‾ \overline{ST} ST为低电平时工作, Y S Y_S YS为使能输出端,通常级联低位芯片的使能端。 Y S Y_S YS和 S T ‾ \overline{ST} ST配合可以实现多级编码器之间的优先级别的控制。 Y E X ‾ \overline{Y_{EX}} YEX为扩展输出端,是控制标志,0表示是编码输出; 1表示不是编码输出。
拓展:
集成3位二进制优先编码器74LS148的级联

8421 BCD码优先编码器(74LS147)
Point 3 译码器
集成二进制译码器(74LS138)

逻辑函数:
Y i = m i S 1 S 2 S 3 ‾ ‾ ‾ Y_i=\overline{m_iS_1\overline{\overline{S_2S_3}}} Yi=miS1S2S3

真值表

Point 4加法器
- 半加器:能对两个1位二进制数进行相加而求得和及进位的逻辑电路称为半加器

2. 全加器:能对两个1位二进制数进行相加并考虑低位来的进位,即相当于3个1位二进制数相加,求得和及进位的逻辑电路称为全加器


3. 可以实现多位二进制数相加的电路称为加法器
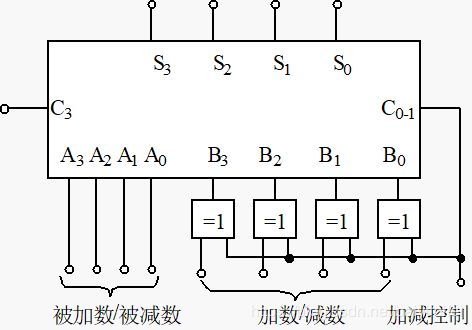
集成二进制四位超前加法器(74LS283)

逻辑函数

其中 C 0 − 1 C_{0-1} C0−1为前一位提供的进位信号, C 3 C_3 C3为向下一位提供的进位信号
级联应用:并行二进制减法器
Point 5 数值比较器
集成数值比较器(74LS85)
Chapter 4 触发器
知识点纲要
- 正确理解各种触发器的电路结构及其动作特点
(直接型、同步型、主从型、边沿型) - 掌握各种触发器的逻辑功能
(RSF、JKF、TF、T`F、DF的功能表、特性方程) - 掌握各种触发器的逻辑功能的相互转换
(JKF、DF转换为TF、T`F)
Point 1 触发器的分类
根据逻辑功能的不同,触发器可以分为RS触发器、D触发器、JK触发器、T和T´触发器;按照结构形式的不同,又可分为基本触发器、同步触发器、主从触发器和边沿触发器。
Point 2 RS触发器
基础RS触发器
动作特点:直接型、RS触发器
电路结构:
功能表:

特性方程:

状态图:

同步RS触发器
动作特点:同步型、RS触发器
电路结构:

其中CP为时钟信号: C P = 0 CP=0 CP=0触发器保持原状态,不变, C P = 1 CP=1 CP=1工作情况与基础触发器相同
功能表:

特性方程
CP=1期间有效
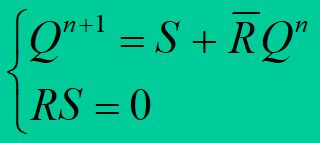
主从RS触发器
动作特点:主从型、RS触发器
电路结构:

特性方程:CP下降沿到来时有效

Point 3 JK触发器
主从JK触发器
动作特点:主从型、JK触发器
电路结构:

特性方程:

功能表:

状态图:

带清0端

Point 4 D触发器
边沿D触发器
动作特点:边沿型、D触发器
电路结构:

特性方程:
下降沿时刻有效

特性表:

逻辑符号:
Point 5 T触发器
在数字电路中,凡在CP时钟脉冲控制下,根据输入信号T取值的不同,具有保持和翻转功能的电路,即当T=0时能保持状态不变,T=1时一定翻转的电路,都称为T触发器。
特征方程:
功能表

由JK触发器转T触发器:

由D触发器转T触发器

Point 6 T’触发器
特征方程:
![]()
功能表:

** 由JK转T触发器**:

由D触发器装T’触发器

Chapter 5 时序逻辑电路
知识点纲要
- 正确理解各种常用时序逻辑电路的逻辑功能(寄存器、计数器)
- 正确理解寄存器的并行置数、移位、 环形移位、扭环形移位等逻辑功能
- 正确理解二进制加/减计数器的逻辑功能
- 正确理解十进制加/减计数器的逻辑功能
- 掌握几块集成中规模集成时序逻辑电路逻辑功能及其应用(74LS161、74LS160、74LS194、74LS290)
Point 1 时序逻辑电路的分类
同步时序电路中,各个触发器的时钟脉冲相同,即电路中有一个统一的时钟脉冲,每来一个时钟脉冲,电路的状态只改变一次。
异步时序电路中,各个触发器的时钟脉冲不同,即电路中没有统一的时钟脉冲来控制电路状态的变化,电路状态改变时,电路中要更新状态的触发器的翻转有先有后,是异步进行的
Point 2 寄存器
双拍工作方式基本寄存器
电路结构:

逻辑函数
(1) C R ‾ = 0 \overline{CR}=0 CR=0,异步清零 Q 3 n Q 2 n Q 1 n Q 0 n = 0000 Q_3^nQ_2^nQ_1^nQ_0^n=0000 Q3nQ2nQ1nQ0n=0000
(2) C R ‾ = 1 \overline{CR}=1 CR=1,cp在上升沿,送数 Q 3 n + 1 Q 2 n + 1 Q 1 n + 1 Q 0 n + 1 = D 3 D 2 D 1 D 0 Q_3^{n+1}Q_2^{n+1}Q_1^{n+1}Q_0^{n+1}=D_3D_2D_1D_0 Q3n+1Q2n+1Q1n+1Q0n+1=D3D2D1D0
(3) C R ‾ = 1 \overline{CR}=1 CR=1,cp在上升沿以外时间 ,保持不变
功能表:

位移寄存器
单向位移寄存器
右移寄存器
左移寄存器
双向寄存器
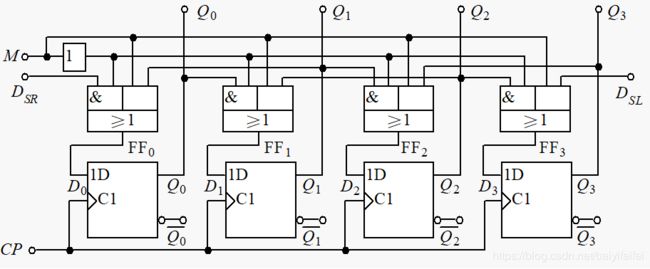
逻辑函数:
M=0时右移:

M=1时左移:
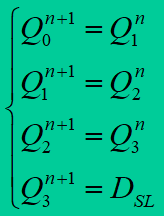
代表芯片:74LS194

功能表

环形计数器
扭环形计数器
Point 3 计数器
异步计数器
三位二进制异步加法计数器
三位二进制异步减法计数器
十进制异步加法计数器
集成二-五-十进制计数器(74LS290)
- R 01 = R 02 = 1 R_{01}=R_{02}=1 R01=R02=1时,异步清零
- S 91 = S 92 = 1 S_{91}=S_{92}=1 S91=S92=1时,异步置9
- C P 0 = C P , C P 1 {CP}_0=CP,CP_1 CP0=CP,CP1悬空,为二进制计数器(以 Q 0 Q_0 Q0表示)
- C P 1 = C P , C P 5 {CP}_1=CP,CP_5 CP1=CP,CP5悬空,为五进制计数器(以 Q 3 Q 2 Q 1 表 示 Q_3Q_2Q_1表示 Q3Q2Q1表示)
- C P 1 = Q 0 , C P 0 = C P CP_1=Q_0,CP_0=CP CP1=Q0,CP0=CP为十进制计数器(以 Q 3 Q 2 Q 1 Q 0 Q_3Q_2Q_1Q_0 Q3Q2Q1Q0)
同步计数器
4位集成二进制同步加法计数器(74LS161)
- R ‾ d = 0 \overline R_d=0 Rd=0异步清0
- R ‾ d = 1 , L D ‾ = 0 \overline R_d=1,\overline{LD}=0 Rd=1,LD=0时置数
- R ‾ d = 1 , L D ‾ = 1 , E T = E P = 1 \overline R_d=1,\overline{LD}=1,E_T=E_P=1 Rd=1,LD=1,ET=EP=1二进制同步计数
- R ‾ d = 1 , L D ‾ = 1 , E T ⋅ E P = 0 \overline R_d=1,\overline{LD}=1,E_T\cdot E_P=0 Rd=1,LD=1,ET⋅EP=0保持
十进制同步加法计数器
Chapter 6 半导体存储器
知识点纲要
- 了解ROM、RAM的特点、分类、电路结构、工作原理
- 掌握ROM实现组合逻辑函数的方法
- 正确理解6116、2716、2864的逻辑功能
- 掌握存储器的存储容量的计算方法
Point 1 ROM只读储存器
特点:在工作时只能从中读出信息,不能写入信息,且断电后其所存信息在仍能保持。
分类:
- 掩膜ROM:不能改写
- PROM:只能改写一次
- ERPROM:可以多次改写
电路结构:
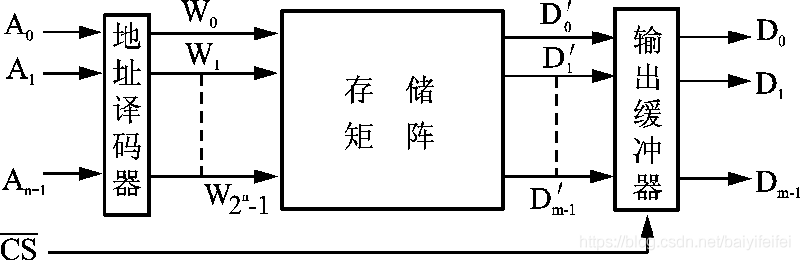
工作原理:

储存容量的计算:
存储容量=字线数×位线数=2n×m(位bit)
Point 2 随机存取存储器RAM
Chapter 7
Point 存储器容量的扩展
位扩展
- 将地址线、读/写线和片选线对应地并联在一起
- 输入、输出分开使用作为字的各个位线
字扩展
Chapter 8 可编程逻辑器件
知识点纲要
- 了解PLA、PAL、GAL的特点、电路结构、工作原理
- 掌握PLA实现组合逻辑函数的方法
- 了解GAL的OLMC及其工作方式
Point 1 现场可编程逻辑阵列PLA
特点:
- 与阵列 + 或阵列+ 输出缓冲器组成
- 逻辑阵列是可编程的
- FPLA 的与逻辑阵列只产生所需要的乘积项。
电路结构:

用于实现逻辑函数
将输出化作最简式,再在与或阵上连接点即可
Point 2 可编程阵列逻辑PAL
特点: PAL器件由可编程的与逻辑阵列、固定的或逻辑阵列和输出电路三部分组成。它采用双极型工艺制作,熔丝编程方式。
电路结构

Point 3 通用阵列逻辑(GAL)
特点:
- GAL采用电可擦除的CMOS(E2CMOS)工艺制造,可反复多次编程
- GAL采用可编程的输出逻辑宏单元OLMC(Output Logic Macro Cell),输出组态灵活,具有很强的通用性
- GAL具有加密功能