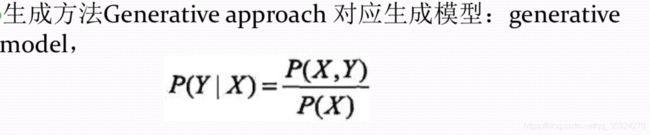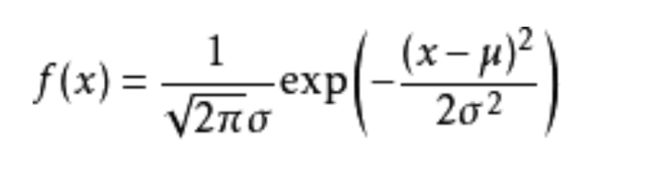《统计学习方法》第一章总结及实现最小二乘法拟合曲线
最近在看李航老师的书,也跟着网上的一些总结以及代码实现学习了,接下来会跟着自己的阅读进度进行更新个人总结。
搭配此门课程的ppt学习会节省挺多时间的,自己也做了一些思维导图不过不是特别好
此学习笔记系列的原代码作者https://github.com/wzyonggege/statistical-learning-method
配置环境python3.5
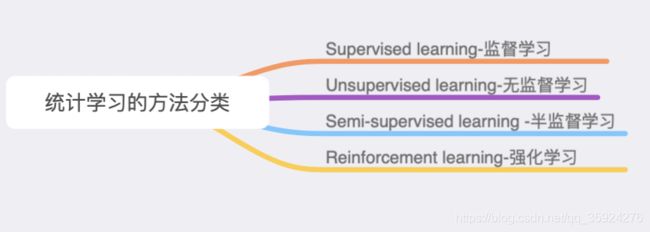
统计学习
分类
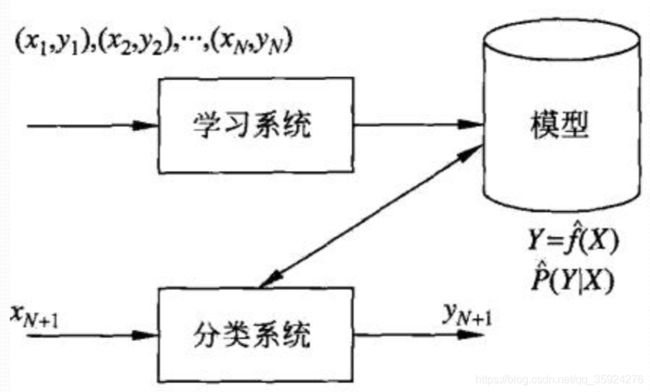
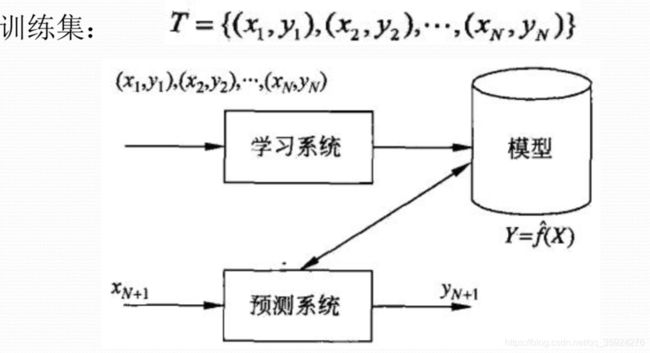
- 监督学习(此书主要讨论监督学习)
- 训练数据 training data
- 模型model----- 假设空间hypothesis
- 评价准则evaluation criterion------策略strategy
- 算法 algorithm
监督学习
-
联合概率分布
训练数据和测试数据被看作是依联合概率分布P(X,Y)独立 同分布产生的。
注: arg 是变元(即自变量argument)的英文缩写。
arg min 就是使后面这个式子达到最小值时的变量的取值
arg max 就是使后面这个式子达到最大值时的变量的取值
统计学习三要素
模型评估与模型选择
如图1.2是多项式函数拟合的情况
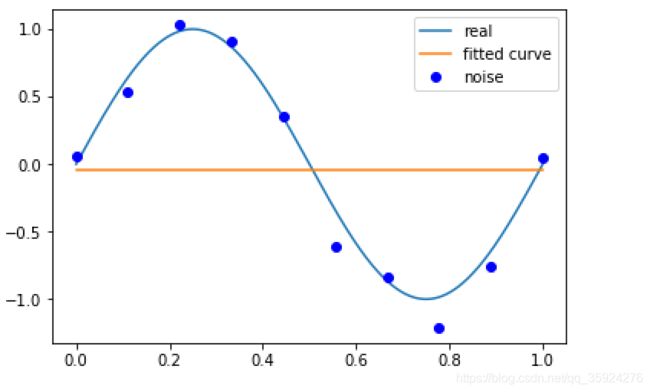
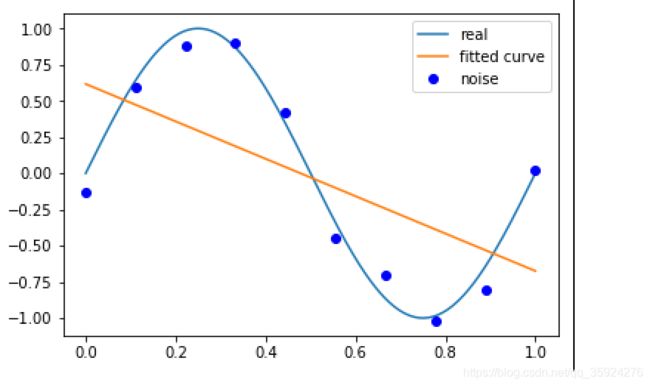
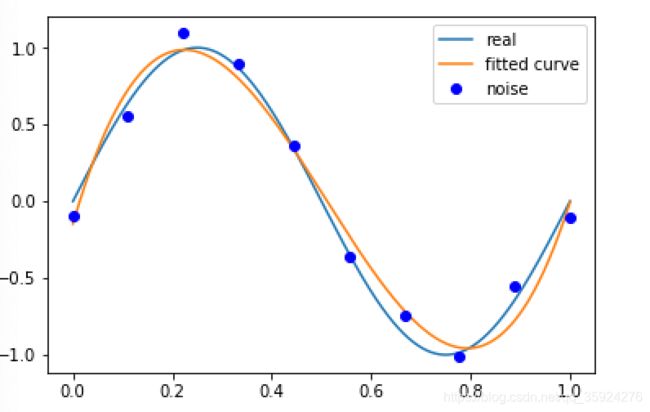
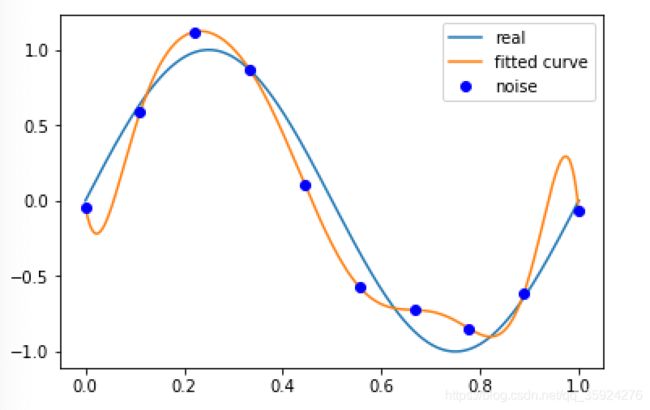
如果M=0, 多项式曲线是一个常数, 数据拟合效果很差。 如果M=1, 多项式曲线是一条直线, 数据拟合效果也很差。 相反,如果M=9, 多项式曲线通过每个数据点, 训练误差为0。 从对给定训练数据拟合的角度来说, 效果是最好的。但是, 因为训练数据本身存在噪声, 这种拟合曲线对未知数据的预测能力往往并不是最好的, 在实际学习中并不可取。 这时过拟合现象就会发生。 这就是说, 模型选择时, 不仅要考虑对已知数据的预测能力, 而且还要考虑对未知数据的预测能力。当M=3时, 多项式曲线对训练数据拟合效果足够好, 模型也比较简单, 是一个较好的选择。
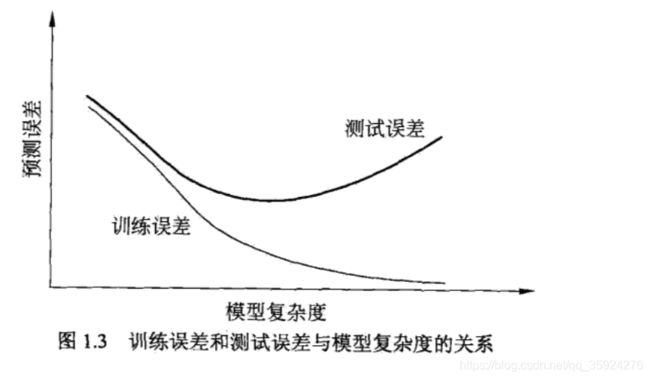
在多项式函数拟合中可以看到, 随着多项式次数(模型复杂度)的增加, 训练误差会减小, 直至趋向于0, 但是测试误差却不如此,它会随着多项式次数(模型复杂度) 的增加先减小而后增大。 而最终的目的是使测试误差达到最小。 这样, 在多项式函数拟合中, 就要选择合适的多项式次数, 以达到这一目的。 这一结论对一般的模型选择也是成立的。
图1.3描述了训练误差和测试误差与模型的复杂度之间的关系。当模型的复杂度增大时, 训练误差会逐渐减小并趋向于0; 而测试误差会先减小, 达到最小值后又增大。当选择的模型复杂度过大时, 过拟合现象就会发生。 这样, 在学习时就要防止过拟合, 进行最优的模型选择, 即选择复杂度适当的模型, 以达到使测试误差最小的学习目的。
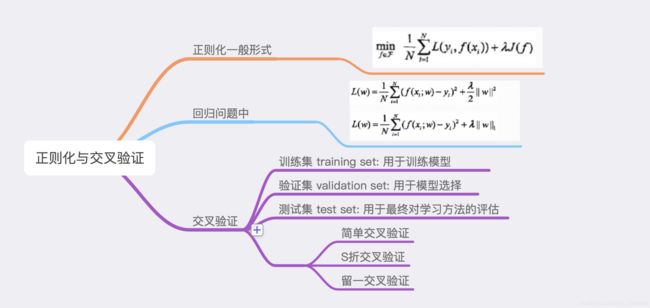
两种常用的模型选择方法: 正则化与交叉验证
在学习到的不同复杂度的模型中, 选择对验证集有最小预测误差的模型。 由于验证集有足够多的数据, 用它对模型进行选择也是有效的。但是, 在许多实际应用中数据是不充足的。 为了选择好的模型,可以采用交叉验证方法。
泛化能力
学习方法的泛化能力(generalization ability) 是指由该方法学习到的模型对未知数据的预测能力, 是学习方法本质上重要的性质。现实中采用最多的办法是通过测试误差来评价学习方法的泛化能力。 但这种评价是依赖于测试数据集的。 因为测试数据集是有限的, 很有可能由此得到的评价结果是不可靠的。 统计学习理论试图从理论上对学习方法的泛化能力进行分析。
生成模型与判别模型
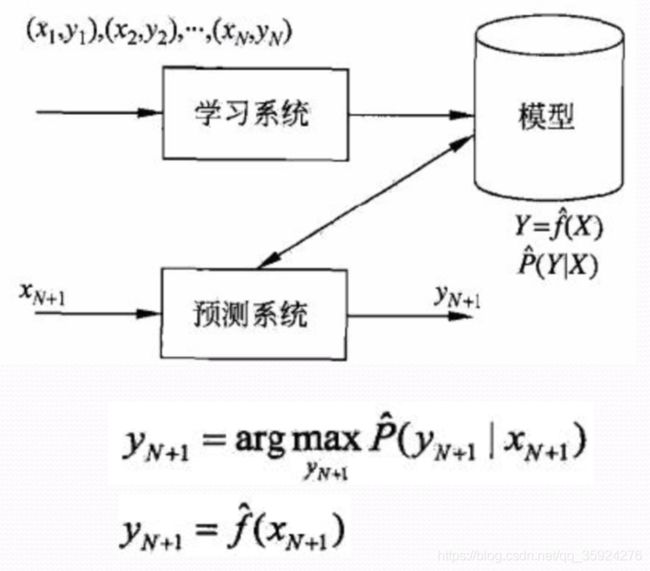
监督学习的任务就是学习一个模型, 应用这一模型, 对给定的输入预测相应的输出。
这个模型的一般形式为决策函数:Y=f(X) 或者条件概率分布:P(Y|X)
监督学习方法又可以分为生成方法(generative approach) 和判别方法(discriminative approach)。所学到的模型分别称为生成模型(generative model) 和判别模型(discriminative model) 。
典型的生成模型有朴素贝叶斯法和隐马尔可夫模型
判别方法由数据直接学习决策函数f(X)或者条件概率分布P(Y|X)作为预测的模型, 即判别模型。判别方法关心的是对给定的输入X,应该预测什么样的输出Y。 典型的判别模型包括: k近邻法、 感知机、 决策树、 逻辑斯谛回归模型、 最大熵模型、 支持向量机、 提升方法和条件随机场等。
生成方法和判别方法的比较
在监督学习中, 生成方法和判别方法各有优缺点, 适合于不同条件下的学习问题。
生成方法:可还原出联合概率分布P(X,Y), 而判别方法不能。 生成方法的收敛速度更快,当样本容量增加的时候,学到的 模型可以更快地收敛于真实模型;当存在隐变量时,仍可以 使用生成方法,而判别方法则不能用。
判别方法:直接学习到条件概率或决策函数,直接进行预 测,往往学习的准确率更高;由于直接学习Y=f(X)或P(Y|X),可对数据进行各种程度上的抽象、定义特征并使用特征,因 此可以简化学习过程。
分类问题
分类是监督学习的一个核心问题。在监督学习中, 当输出变量Y取有限个离散值时, 预测问题便成为分类问题。
这时, 输入变量X可以是离散的, 也可以是连续的。
评价分类器性能的指标一般是分类准确率(accuracy) , 其定义是: 对于给定的测试数据集, 分类器正确分类的样本数与总样本数之比。 也就是损失函数是0-1损失时测试数据集上的准确率(见书中公式(1.17) ) 。
精确率(precision) 与召回率(recall)
对于二类分类问题常用的评价指标是精确率(precision) 与召回率(recall) 。
通常以关注的类为正类, 其他类为负类, 分类器在测试数据集上的预测或正确或不正确, 4种情况出现的总数分别记作:
TP——将正类预测为正类数;
FN——将正类预测为负类数;
FP——将负类预测为正类数;
TN——将负类预测为负类数。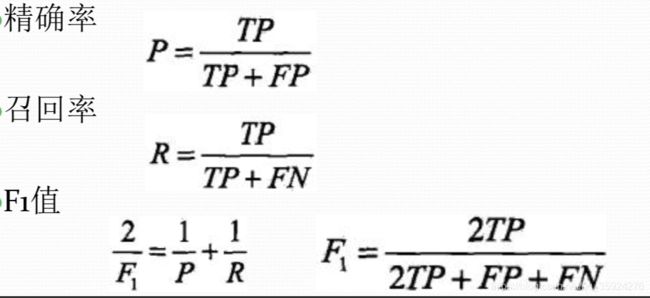
F1值, 是精确率和召回率的调和均值。精确率和召回率都高时, F1值也会高。
标注问题
标注(tagging) 也是一个监督学习问题。可以认为标注问题是分类问题的一个推广, 标注问题又是更复杂的结构预测问题的简单形式。标注问题的输入是一个观测序列, 输出是一个标记序列或状态序列。标注问题的目标在于学习一个模型, 使它能够对观测序列给出标记序列作为预测。 注意, 可能的标记个数是有限的, 但其组合所成的标记序列的个数是依序列长度呈指数级增长的。
评价标注模型的指标与评价分类模型的指标一样, 常用的有标注准确率、 精确率和召回率。 其定义与分类模型相同。
标注常用的统计学习方法有: 隐马尔可夫模型、 条件随机场。
回归问题
回归模型是表示从输入变量到输出变量之间映射的函数.回归问题的学习等价于函数拟合。回归问题分为学习和预测两个阶段
例子:标记表示名词短语的“开始”、“结束”或“其他”(分别以B, E, O表示)
输入:At Microsoft Research, we have an insatiable curiosity and the desire to create new technology that will help define the computing experience.
输出:At/O Microsoft/B Research/E, we/O have/O an/O insatiable/6 curiosity/E and/O the/O desire/BE to/O create/O new/B technology/E that/O will/O help/O define/O the/O computing/B experience/E.
回归学习最常用的损失函数是平方损失函数,在此情况 下,回归问题可以由 著名的最小二乘法(least squares)求解。
在本书的学习中称由决策函数表示的模型为非概率模型,由条件概率表示的模型为概率模型。
举例:我们用目标函数y=sin2πx, 加上一个正太分布的噪音干扰,用多项式去拟合【例1.1 11页】
import numpy as np
import scipy as sp
from scipy.optimize import leastsq
#引入最小二乘法least-square fitting
#最优化函数库optiminzation
#scipy.optimization子模块提供了函数最小值(标量或多维)、
# 曲线拟合和寻找等式的根的有用算法。
import matplotlib.pyplot as plt
#%matplotlib inline
#ps: numpy.poly1d([1,2,3]) 生成 1x^2+2x^1+3x^0
#目标函数y=sin(2πx)
def real_func(x):
return np.sin(2*np.pi*x)
#拟合函数
def fit_func(p,x):
f = np.poly1d(p)
return f(x)
#残差函数
def residuala_func(p,x,y):
ret = fit_func(p,x) -y
return ret
#随机选取10个点
x = np.linspace(0,1,10)
#画图时需要的连续点
x_points = np.linspace(0,1,1000)
#目标函数
y_ = real_func(x)
#添加正态分布噪声后的函数
y = [np.random.normal(0,0.1) + y1 for y1 in y_]
def fitting(M=0):
#M为多项式参数个数
#n为多项式的次数
p_init = np.random.rand(M+1)
#随机初始化多项式参数
p_lsq= leastsq(residuala_func,p_init,args=(x,y))
#最小二乘法
# 调用leastsq进行数据拟合, residuals为计算误差的函数
# p0为拟合参数的初始值,
# # args为需要拟合的实验数据
# plsq = leastsq(residuals, p0, args=(y1, x))
#可视化
plt.pyplot.plot(x_points,real_func(x_points),label = 'real')
plt.pyplot.plot(x_points,fit_func(p_lsq[0],x_points),label = 'fitted curve')
plt.pyplot.plot(x,y,'bo',label = 'noise')
plt.pyplot.legend()
return p_lsq
一些小注释
# numpy.random.normal(loc=0.0, scale=1.0, size=None)
#loc:float概率分布的均值,对应着整个分布的中心center
#¥scale:float概率分布的标准差,对应于分布的宽度,scale越大越矮胖,scale越小,越瘦高
#size:int or tuple of ints输出的shape,默认为None,只输出一个值
我们更经常会用到np.random.randn(size)所谓标准正太分布(μ=0, σ=1),对应于np.random.normal(loc=0, scale=1, size)
高斯分布的概率密度函数
p_lsq_0 = fitting(M=0)
p_lsq_0 = fitting(M=1)
p_lsq_0 = fitting(M=3)p_lsq_0 = fitting(M=9)