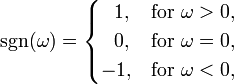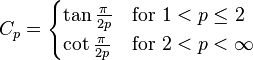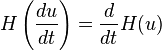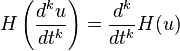Hilbert变换及谱分析

在数学与信号处理的领域中，一个实数值函数的希尔伯特转换(Hilbert transform)——在此标示为——是将信号与做卷积，以得到。因此，希尔伯特转换结果可以被解读为输入是的线性非时变系统(linear time invariant system)的输出，而此一系统的脉冲响应为。这是一项有用的数学，用在描述一个以实数值载波做调制的信号之复数包络(complex envelope)，出现在通讯理论（应用方面的详述请见下文。）

希尔伯特转换是以著名数学家大卫·希尔伯特(David Hilbert)来命名。

定义

希尔伯特转换定义如下：

其中

并考虑此积分为柯西主值(Cauchy principal value)，其避免掉在以及等处的奇点。

另外要指出的是：若，则可被定义，且属于；其中。

频率响应

希尔伯特转换之频率响应由傅立叶变换给出：

,  

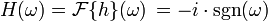其中

• 是傅立叶变换，
• i (有时写作j )是虚数单位，
• 是角频率，以及
• 

即为符号函数。

既然：

,

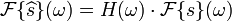希尔伯特转换会将负频率成分偏移+90°，而正频率成分偏移−90°。

反（逆）希尔伯特转换

我们也注意到：。因此将上面方程式乘上，可得到：

从中，可以看出反（逆）希尔伯特转换

特性

边界

若 1<p<∞，则 L^p(R)之希尔伯特转换为一有界算子，表示存在一常数C_p使得

对所有 u∈L^p(R)。这个定理由Riesz (1928， VII)所推得；请一并参见Titchmarsh (1948， Theorem 101)。 最佳常数C_p可由下列算式得到:

这个结果由（Pichorides 1972）所推得；请一并参见Grafakos (2004， Remark 4.1.8)。上述最佳常数计算方式应用在周期性希尔伯特转换一样成立。

希尔伯特转换的边界指的是 L^p(R) 对称级数运算子对于在 L^p(R) 之中 f 的收敛

请参见（Duoandikoetxea 2000，p.59）。

反自伴性

希尔伯特转换为一反自伴算子，连结 L^p(R) 与其对偶空间 L^q(R)，其中 p 和 q 为 赫尔德共轭且 1 < p,q < ∞. 以符号表示

对 u ∈ L^p(R) 且 v ∈ L^q(R) （Titchmarsh 1948，Theorem 102）.

逆转换

希尔伯特转换为一反-对合 （Titchmarsh 1948，p.120），意即

假定每一转换皆完整定义过。由于 H 保存了 L^p(R)空间，这特别代表希尔伯特转换在 L^p(R) 上是不可逆的，且

微分

正式上，一个式子其希尔伯特转换的微分即为其微分的希尔伯特转换，意即这两者是可以交换的线性算子

此一特性亦可迭代

给定 u 以及其前k次微分皆属于L^p(R) （Pandey 1996，§3.3）空间，此项论述为严格成立。在频域上可以轻易验证这件事情，由于微分在频域上即为与 ω 之乘积。

旋积

希尔伯特转换可表示为与一调节分布之旋积 （Duistermaat & Kolk 2010，p.211）

因此可如此表示

然而，事前此特性可能只有对紧支撑之分布 u定义。由于紧支撑函数在 L^p 上是稠密的，因此此项特性可能严格成立。另一角度来看，也可使用 h(t) 其微分之特性来证明

在大部分的用途，希尔伯特转换可被视为是一旋积。举例而言，旋积与希尔伯特转换具备下列可交换的特性

若 u 和 v 为紧支撑分布，则此项论述严格成立，在这个状况下

不变性

希尔伯特转换在空间 L²(R) 上有下列特性

• 可与算子 T_aƒ(x) = ƒ(x + a) 交换，对所有实数 a
• 可与算子 M_λƒ(x) = ƒ(λx) 交换，对所有 λ > 0
• 可与镜射 Rƒ(x) = ƒ(−x) 反交换

实际上，有更大一部分的算子可与希尔伯特转换交换。群组 SL(2,R) 由幺正算符 U_g 可在空间 L²(R) 上由以下式子表示

% Hilbert transform testing
clc
clear all
close all

ts = 0.001;
fs = 1/ts;
N = 200;
f = 50;
k = 0:N-1;
t = k*ts;

% signal transform
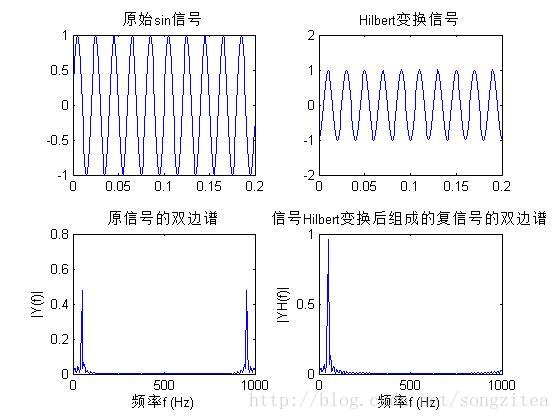
% 结论：sin信号Hilbert变换后为cos信号
y = sin(2*pi*f*t);
yh = hilbert(y);    % matlab函数得到信号是合成的复信号
yi = imag(yh);      % 虚部为书上定义的Hilbert变换

figure
subplot(221)
plot(t, y)
title('原始sin信号')
subplot(222)
plot(t, yi)
title('Hilbert变换信号')

% 检验两次Hilbert变换的结果（理论上为原信号的负值）
% 结论：两次Hilbert变换的结果为原信号的负值
yih = hilbert(yi);
yii = imag(yih);
max(y + yii)

% 信号与其Hilbert变换的正交性
% 结论：Hilbert变换后的信号与原信号正交
sum(y.*yi)

% 谱分析
% 结论：Hilbert变换后合成的复信号的谱没有大于奈氏频率的频谱，即其谱为单边的
NFFT = 2^nextpow2(N);
f = fs*linspace(0,1,NFFT);
Y = fft(y, NFFT)/N;
YH = fft(yh, NFFT)/N;

%figure
subplot(223)
plot(f,abs(Y))
title('原信号的双边谱')
xlabel('频率f (Hz)')
ylabel('|Y(f)|')
subplot(224)
plot(f,abs(YH))
title('信号Hilbert变换后组成的复信号的双边谱')
xlabel('频率f (Hz)')
ylabel('|YH(f)|')

第一个程序效果如下