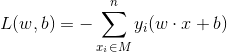统计学习第二章（感知机）知识总结

2.1感知机学习模型

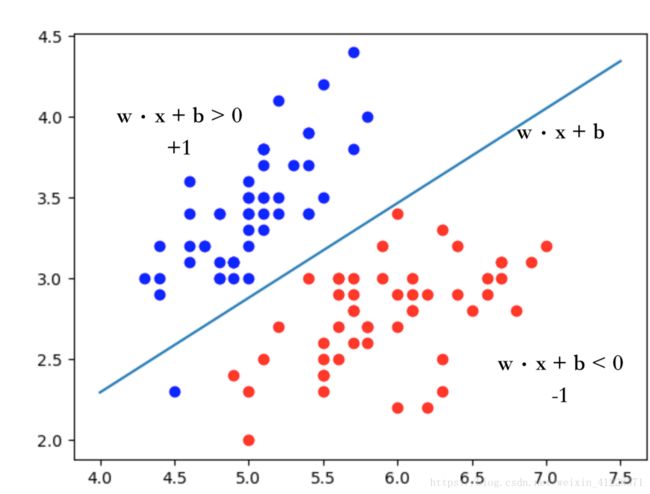
         概述：感知机是一种线性分类模型，通过特征空间中的超平面S将特征空间划分为两部分，w是超平面的法向量，b是特征空间的截距。为了方便理解，把超平面S定为二维图像中的线，这样可以根据坐标来理解分类原理，如下图：

                       

         图中可以看到蓝色和红色分别代表正例和反例，当w·x+b>0时为正例，当w·x+b<0时为反例。

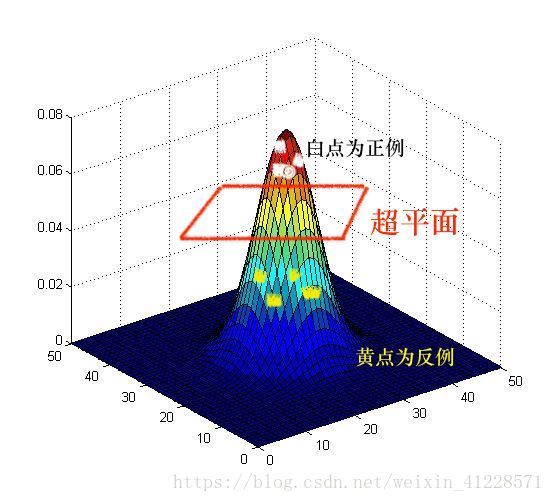
         下面来把这个二维的图像上升到三维，来解释一下超平面（支持向量机也用到该知识点）

                                   

         输入空间（特征空间）包括实例中的所有特征，例如：好瓜、坏瓜分类中的色泽、根蒂、敲声。

         输出空间表示实例的类别，例如：好瓜、坏瓜。

         假设空间（由输入空间到输出空间的映射）如下函数：

                                                    

 

2.2感知机学习策略

         感知机的学习策略简单来讲就是求各个误分类数据点到超平面的总距离。

         下面讨论一下正常数据和误分类点：

          正常数据： w·x + b > 0         = +1

                             w·x + b < 0         = -1

          误分类点：w·x + b > 0         = -1

                             w·x + b < 0         = +1

          误分类点  到超平面的距离：

                                                            

          各个误分类点到超平面的总距离：

                                                           

          因为  中的||w||是范数的意思表示全部w向量的平方和的开方，可以看作是一个常数所以不考虑，参考了一下

         感知机中损失函数1/||w||为什么可以不考虑（或直接忽略）？

         最后得到了感知机的损失函数：

                                                          

          之后只要最小化这个损失函数就可以了。

 

2.3感知机学习算法

2.3.1算法的原始形式

          感知机的学习算法就是将误分类点到超平面的距离最小化。最小化的方式为梯度下降。因为梯度下降是一种凸优化的方式来得到全局最小值。

          梯度下降，顺着梯度的负方向更新损失函数（负梯度方向，斜率下降最快）。

          w的梯度:

                                                            

          b的梯度：

                                                            

          负梯度方向更新：

                                                           

                                                            

          算法步骤：

                          （1）选取  ,

                          （2）在训练集中选取数据(,)

                          （3）如果  （x和y异号，为误差点），更新

                                                            

                                                            

                          （4）转至（2），直至训练集中没有误分类点

2.3.2算法的对偶形式

          由原来求最小化误分类点到超平面距离变为求最小化更新次数。

          对误分类点通过

                                                            

                                                            

          逐步修改w,b，设修改n次，则w,b关于误分类点的增量分别是和，这里,这样通过学习后公式变为：

                                                            

                                                            

          当时，表示第i个实例点由于误分类而进行更新的次数，实例点更新次数越多，意味着它距离分离超平面越近，也就越难正确分类。

           对偶形式的感知机模型：

                                                           

           算法步骤：

                          （1），

                          （2）在训练集中选取数据(,)

                          （3）如果  （x和y异号，为误差点），更新

                                                            

                                                            

                          （4）转至（2），直至训练集中没有误分类点

 

2.4python实现感知机鸢尾花分类

         选取鸢尾花数据中前两个参数作为输入（特征）空间，选取setosa和versicolor两种类别进行简单分类

         代码如下：

import numpy as np
import matplotlib.pyplot as plt
import pandas as pd


def iris_type(s):
    it = {b'Iris-setosa': -1, b'Iris-versicolor': 1, b'Iris-virginica': 2}#python3在读取数据的时候，需要一个编码，所以在string前面加一个b
    return it[s]

path = '/Desktop/iris.data'  # 数据文件路径，网上的iris数据集很多
data = np.loadtxt(path, dtype=float, delimiter=',', converters={4: iris_type})     
 #用numpy中的loadtxt函数把数据的类型改为float，文件的类型改为txt文档，并且调用def iris_type(s)函数把鸢尾花种类用数字代替，方便后面对数据进行条件选择

for j in range(len(data)):      #双层循环，因为一次循环以后矩阵会改变，所以要重新遍历一遍矩阵
    for i in range(len(data)):
        if data[i, 4:] == 2:
            data = np.delete(data, i, 0)
            break

x,y = np.split(data,(4,),axis=1)     #给x，y赋值
x = x[:,0:2]                         #x取鸢尾花数据集中前两个特征值

#画数据集的样本分布图：正例为蓝色，反例为红色
plt.figure()
for i in range(len(x)):
    if y[i] == 1:
        plt.plot(x[i][0], x[i][1], 'ro')
    else:
        plt.plot(x[i][0], x[i][1], 'bo')

#初始化w，b和delta，经过调参，发现当初始化w为[5,0]的时候，该模型的拟合效果最佳
w = np.array([5,0])
b = 0
delta = 1

#循环条件更新
for i in range(len(x)):
    choice = -1
    for j in range(len(x)):
        if y[j] != np.sign(np.dot(w,x[0])+b):
            choice = j
            break
        if choice == -1:
            break
    w = w + delta * y[choice] * x[choice]
    b = b + delta * y[choice]

#画学习后的超平面，因为特征值只选取了两位，则超平面为二维的线，最后保存图片
line_x = [4,7.5]
line_y = [0,0]
for i in range(len(line_x)):
    line_y[i] = (-w[0] * line_x[i] - b) / w[1]
plt.plot(line_x, line_y)
plt.savefig("picture1.png")

           结果如下：