人工智能——利用Python编程,求解多元函数极值和回归问题的几种方法
人工智能实验————利用Python编程,求解多元函数极值和回归问题的几种方法
一、牛顿法
1.原理详解
高次方程没有通解,可以依靠牛顿迭代法来求解。没有根式解不意味着方程解不出来,数学家也提供了很多方法,牛顿迭代法就是其中一种。
首先,切线是曲线的线性逼近。可以通过研究简单切线的解来近似的逼近复杂曲线的解随便找一个曲线上的A点(为什么随便找,根据切线是切点附近的曲线的近似,应该在根点附近找,但是很显然我们现在还不知道根点在哪里),做一个切线,切线的根(就是和x轴的交点)与曲线的根,还有一定的距离。我们从这个切线的根出发,做一根垂线,和曲线相交于B点,继续重复刚才的工作;B点比之前A点更接近曲线的根点,我们继续重复刚才的工作;经过多次迭代后会越来越接近曲线的根,从数学的角度上说,切线收敛了,此时我们就得到了一个曲线近似的解。
2.题目实例——牛顿法解简单的一元函数
from sympy import *
# step为迭代步数,x0为初始位置,obj为要求极值的函数
def newtons(step, x0, obj):
i = 1 # 记录迭代次数的变量
x0 = float(x0) # 浮点数计算更快
obj_deri = diff(obj, x) # 定义一阶导数,对应上述公式
obj_sec_deri = diff(obj, x, 2) # 定义二阶导数,对应上述公式
while i <= step:
if i == 1:
# 第一次迭代的更新公式
xnew = x0 - (obj_deri.subs(x, x0)/obj_sec_deri.subs(x, x0))
print('迭代第%d次:%.5f' %(i, xnew))
i = i + 1
else:
#后续迭代的更新公式
xnew = xnew - (obj_deri.subs(x, xnew)/obj_sec_deri.subs(x, xnew))
print('迭代第%d次:%.5f' % (i, xnew))
i = i + 1
return xnew
x = symbols("x") # x为字符变量
result = newtons(50, 10, x**6+x)
print('最佳迭代的位置:%.5f' %result)
迭代第1次:8.00000
迭代第2次:6.39999
迭代第3次:5.11997
迭代第4次:4.09593
迭代第5次:3.27662
迭代第6次:2.62101
迭代第7次:2.09610
迭代第8次:1.67515
迭代第9次:1.33589
迭代第10次:1.05825
迭代第11次:0.82002
迭代第12次:0.58229
迭代第13次:0.17590
迭代第14次:-34.68063
迭代第15次:-27.74450
迭代第16次:-22.19560
迭代第17次:-17.75648
迭代第18次:-14.20519
迭代第19次:-11.36415
迭代第20次:-9.09132
迭代第21次:-7.27306
迭代第22次:-5.81846
迭代第23次:-4.65480
迭代第24次:-3.72391
迭代第25次:-2.97930
迭代第26次:-2.38386
迭代第27次:-1.90812
迭代第28次:-1.52901
迭代第29次:-1.22931
迭代第30次:-0.99804
迭代第31次:-0.83203
迭代第32次:-0.73518
迭代第33次:-0.70225
迭代第34次:-0.69886
迭代第35次:-0.69883
迭代第36次:-0.69883
迭代第37次:-0.69883
迭代第38次:-0.69883
迭代第39次:-0.69883
迭代第40次:-0.69883
迭代第41次:-0.69883
迭代第42次:-0.69883
迭代第43次:-0.69883
迭代第44次:-0.69883
迭代第45次:-0.69883
迭代第46次:-0.69883
迭代第47次:-0.69883
迭代第48次:-0.69883
迭代第49次:-0.69883
迭代第50次:-0.69883
最佳迭代的位置:-0.69883
二、梯度下降法
1.原理详解
关于梯度下降算法的直观理解,我们以一个人下山为例。比如刚开始的初始位置是山顶位置,那么现在的问题是该如何达到山底呢?按照梯度下降算法的思想,它将按如下操作达到最低点:
第一步,明确自己现在所处的位置
第二步,找到相对于该位置而言下降最快的方向
第三步, 沿着第二步找到的方向走一小步,到达一个新的位置,此时的位置肯定比原来低
第四部, 回到第一步
第五步,终止于最低点
按照以上5步,最终达到最低点,这就是梯度下降的完整流程。
梯度下降的基本过程就和下山的场景很类似。
首先,我们有一个可微分的函数。这个函数就代表着一座山。我们的目标就是找到这个函数的最小值,也就是山底。根据之前的场景假设,最快的下山的方式就是找到当前位置最陡峭的方向,然后沿着此方向向下走,对应到函数中,就是找到给定点的梯度 ,然后朝着梯度相反的方向,就能让函数值下降的最快!因为梯度的方向就是函数之变化最快的方向(在后面会详细解释)
所以,我们重复利用这个方法,反复求取梯度,最后就能到达局部的最小值,这就类似于我们下山的过程。而求取梯度就确定了最陡峭的方向,也就是场景中测量方向的手段
2.题目实例
实例一
import numpy as np
import matplotlib.pyplot as plt
import matplotlib as mpl
import math
from mpl_toolkits.mplot3d import Axes3D
import warnings
导入一些必要的库特别是用于3D绘图的库
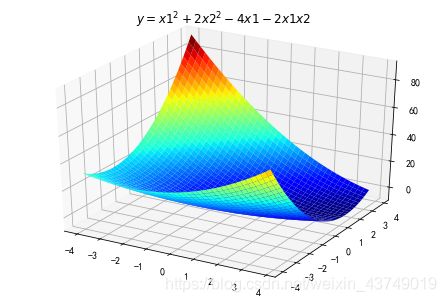
def f2(x1,x2):
return x1*x1+2*x2*x2-4*x1-2*x1*x2
X1 = np.arange(-4,4,0.2)
X2 = np.arange(-4,4,0.2)
X1, X2 = np.meshgrid(X1, X2) # 生成xv、yv,将X1、X2变成n*m的矩阵,方便后面绘图
Y = np.array(list(map(lambda t : f2(t[0],t[1]),zip(X1.flatten(),X2.flatten()))))
Y.shape = X1.shape # 1600的Y图还原成原来的(40,40)
%matplotlib inline
#作图
fig = plt.figure(facecolor='w')
ax = Axes3D(fig)
ax.plot_surface(X1,X2,Y,rstride=1,cstride=1,cmap=plt.cm.jet)
ax.set_title(u'$ y = x1^2+2x2^2-4x1-2x1x2 $')
plt.show()
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import numpy as np
def Fun(x,y):#原函数
return x-y+2*x*x+2*x*y+y*y
def PxFun(x,y):#偏x导
return 1+4*x+2*y
def PyFun(x,y):#偏y导
return -1+2*x+2*y
#初始化
fig=plt.figure()#figure对象
ax=Axes3D(fig)#Axes3D对象
X,Y=np.mgrid[-2:2:40j,-2:2:40j]#取样并作满射联合
Z=Fun(X,Y)#取样点Z坐标打表
ax.plot_surface(X,Y,Z,rstride=1,cstride=1,cmap="rainbow")
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_zlabel('z')
#梯度下降
step=0.0008#下降系数
x=0
y=0#初始选取一个点
tag_x=[x]
tag_y=[y]
tag_z=[Fun(x,y)]#三个坐标分别打入表中,该表用于绘制点
new_x=x
new_y=y
Over=False
while Over==False:
new_x-=step*PxFun(x,y)
new_y-=step*PyFun(x,y)#分别作梯度下降
if Fun(x,y)-Fun(new_x,new_y)<7e-9:#精度
Over=True
x=new_x
y=new_y#更新旧点
tag_x.append(x)
tag_y.append(y)
tag_z.append(Fun(x,y))#新点三个坐标打入表中
#绘制点/输出坐标
ax.plot(tag_x,tag_y,tag_z,'r.')
plt.title('(x,y)~('+str(x)+","+str(y)+')')
plt.show()
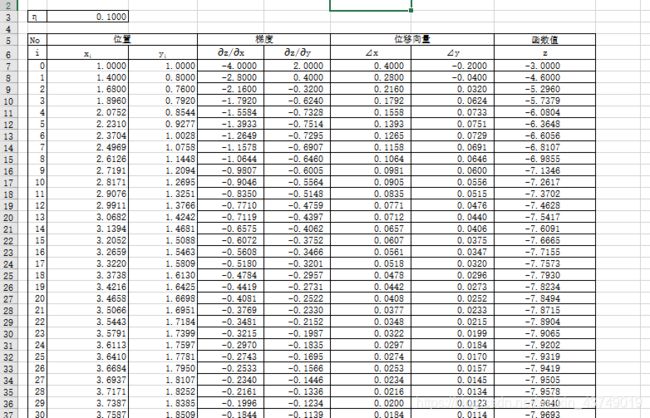
同Excel中的梯度求解进行比较
实例二 用梯度下降法求多元线性回归问题
import numpy as np
from matplotlib import pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
data=np.genfromtxt('1.csv',delimiter=',')
x_data=data[:,:-1]
y_data=data[:,2]
#定义学习率、斜率、截据
#设方程为y=theta1x1+theta2x2+theta0
lr=0.00001
theta0=0
theta1=0
theta2=0
#定义最大迭代次数,因为梯度下降法是在不断迭代更新k与b
epochs=10000
#定义最小二乘法函数-损失函数(代价函数)
def compute_error(theta0,theta1,theta2,x_data,y_data):
totalerror=0
for i in range(0,len(x_data)):#定义一共有多少样本点
totalerror=totalerror+(y_data[i]-(theta1*x_data[i,0]+theta2*x_data[i,1]+theta0))**2
return totalerror/float(len(x_data))/2
#梯度下降算法求解参数
def gradient_descent_runner(x_data,y_data,theta0,theta1,theta2,lr,epochs):
m=len(x_data)
for i in range(epochs):
theta0_grad=0
theta1_grad=0
theta2_grad=0
for j in range(0,m):
theta0_grad-=(1/m)*(-(theta1*x_data[j,0]+theta2*x_data[j,1]+theta2)+y_data[j])
theta1_grad-=(1/m)*x_data[j,0]*(-(theta1*x_data[j,0]+theta2*x_data[j,1]+theta0)+y_data[j])
theta2_grad-=(1/m)*x_data[j,1]*(-(theta1*x_data[j,0]+theta2*x_data[j,1]+theta0)+y_data[j])
theta0=theta0-lr*theta0_grad
theta1=theta1-lr*theta1_grad
theta2=theta2-lr*theta2_grad
return theta0,theta1,theta2
#进行迭代求解
theta0,theta1,theta2=gradient_descent_runner(x_data,y_data,theta0,theta1,theta2,lr,epochs)
print('结果:迭代次数:{0} 学习率:{1}之后 a0={2},a1={3},a2={4},代价函数为{5}'.format(epochs,lr,theta0,theta1,theta2,compute_error(theta0,theta1,theta2,x_data,y_data)))
print("多元线性回归方程为:y=",theta1,"X1+",theta2,"X2+",theta0)
#画图
ax=plt.figure().add_subplot(111,projection='3d')
ax.scatter(x_data[:,0],x_data[:,1],y_data,c='r',marker='o')
x0=x_data[:,0]
x1=x_data[:,1]
#生成网格矩阵
x0,x1=np.meshgrid(x0,x1)
z=theta0+theta1*x0+theta2*x1
#画3d图
ax.plot_surface(x0,x1,z)
ax.set_xlabel('area')
ax.set_ylabel('distance')
ax.set_zlabel("Monthly turnover")
plt.show()
结果:迭代次数:10000 学习率:1e-05之后 a0=5.3774162274868,a1=45.0533119768975,a2=-0.19626929358281256,代价函数为366.7314528822914
多元线性回归方程为:y= 45.0533119768975 X1+ -0.19626929358281256 X2+ 5.3774162274868
三、最小二乘法
1.原理详解
最小二乘法(又称最小平方法)是一种数学优化技术。它通过最小化误差的平方和寻找数据的最佳函数匹配。利用最小二乘法可以简便地求得未知的数据,并使得这些求得的数据与实际数据之间误差的平方和为最小。最小二乘法还可用于曲线拟合
以最简单的一元线性模型来解释最小二乘法。什么是一元线性模型呢?监督学习中,如果预测的变量是离散的,我们称其为分类(如决策树,支持向量机等),如果预测的变量是连续的,我们称其为回归。回归分析中,如果只包括一个自变量和一个因变量,且二者的关系可用一条直线近似表示,这种回归分析称为一元线性回归分析。如果回归分析中包括两个或两个以上的自变量,且因变量和自变量之间是线性关系,则称为多元线性回归分析。对于二维空间线性是一条直线;对于三维空间线性是一个平面,对于多维空间线性是一个超平面。
对于一元线性回归模型, 假设从总体中获取了n组观察值(X1,Y1),(X2,Y2), …,(Xn,Yn)。对于平面中的这n个点,可以使用无数条曲线来拟合。要求样本回归函数尽可能好地拟合这组值。综合起来看,这条直线处于样本数据的中心位置最合理。 选择最佳拟合曲线的标准可以确定为:使总的拟合误差(即总残差)达到最小。有以下三个标准可以选择:
(1)用“残差和最小”确定直线位置是一个途径。但很快发现计算“残差和”存在相互抵消的问题。
(2)用“残差绝对值和最小”确定直线位置也是一个途径。但绝对值的计算比较麻烦。
(3)最小二乘法的原则是以“残差平方和最小”确定直线位置。用最小二乘法除了计算比较方便外,得到的估计量还具有优良特性。这种方法对异常值非常敏感。
最常用的是普通最小二乘法:所选择的回归模型应该使所有观察值的残差平方和达到最小。
2.题目实例
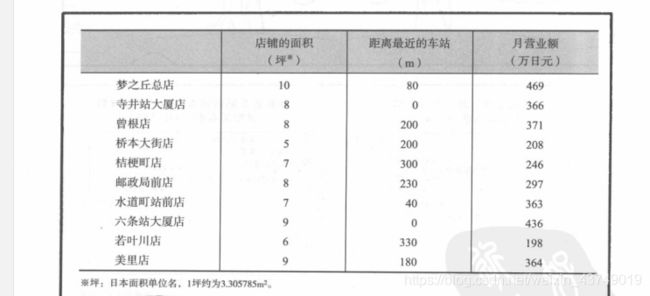
实例一 最小二乘法求解多元线性回归 题目同上实例二
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
import seaborn as sns
%matplotlib inline
data = np.genfromtxt("1.csv",delimiter=",")
X1=data[0:10,0]#面积
X2=data[0:10,1]#离车站的距离
Y=data[0:10,2]#月营业额
#将因变量赋值给矩阵Y1
Y1=np.array([Y]).T
#为自变量系数矩阵X赋值
X11=np.array([X1]).T
X22=np.array([X2]).T
A=np.array([[1],[1],[1],[1],[1],[1],[1],[1],[1],[1]])#创建系数矩阵
B=np.hstack((A,X11))#将矩阵a与矩阵X11合并为矩阵b
X=np.hstack((B,X22))#将矩阵b与矩阵X22合并为矩阵X
#求矩阵X的转置矩阵
X_=X.T
#求矩阵X与他的转置矩阵的X_的乘积
X_X=np.dot(X_,X)
#求矩阵X与他的转置矩阵的X_的乘积的逆矩阵
X_X_=np.linalg.inv(X_X)
#求解系数矩阵W,分别对应截距b、a1、和a2
W=np.dot(np.dot((X_X_),(X_)),Y1)
b=W[0][0]
a1=W[1][0]
a2=W[2][0]
print("系数a1={:.1f}".format(a1))
print("系数a2={:.1f}".format(a2))
print("截距为={:.1f}".format(b))
print("多元线性回归方程为:y={:.1f}".format(a1),"X1+ {:.1f}".format(a2),"X2+{:.1f}".format(b))
#画出线性回归分析图
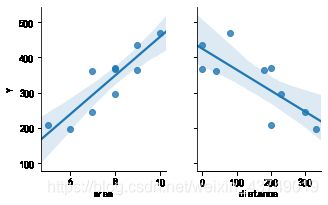
data1=pd.read_excel('1.xlsx')
sns.pairplot(data1, x_vars=['area','distance'], y_vars='Y', height=3, aspect=0.8, kind='reg')
plt.show()
#求月销售量Y的和以及平均值y1
sumy=0#因变量的和
y1=0#因变量的平均值
for i in range(0,len(Y)):
sumy=sumy+Y[i]
y1=sumy/len(Y)
#求月销售额y-他的平均值的和
y_y1=0#y-y1的值的和
for i in range(0,len(Y)):
y_y1=y_y1+(Y[i]-y1)
print("营业额-营业额平均值的和为:{:.1f}".format(y_y1))
#求预测值sales1
sales1=[]
for i in range(0,len(Y)):
sales1.append(a1*X1[i]+a2*X2[i]+b)
#求预测值的平均值y2
y2=0
sumy2=0
for i in range(len(sales1)):
sumy2=sumy2+sales1[i]
y2=sumy2/len(sales1)
#求预测值-平均值的和y11_y2
y11_y2=0
for i in range(0,len(sales1)):
y11_y2=y11_y2+(sales1[i]-y2)
print("预测营业额-预测营业额平均值的和为:{:.1f}".format(y11_y2))
#求月销售额y-他的平均值的平方和
Syy=0#y-y1的值的平方和
for i in range(0,len(Y)):
Syy=Syy+((Y[i]-y1)*(Y[i]-y1))
print("Syy={:.1f}".format(Syy))
#求y1-y1平均的平方和
Sy1y1=0
for i in range(0,len(sales1)):
Sy1y1=Sy1y1+((sales1[i]-y2)*(sales1[i]-y2))
print("Sy1y1={:.1f}".format(Sy1y1))
#(y1-y1平均)*(y-y平均)
Syy1=0
for i in range(0,len(sales1)):
Syy1=Syy1+((Y[i]-y1)*(sales1[i]-y2))
print("Syy1={:.1f}".format(Syy1))
#求y-y1的平方Se
Se=0
for i in range(0,len(sales1)):
Se=Se+((Y[i]-y2)*(Y[i]-y2))
print("Se={:.1f}".format(Se))
#求R
R=Syy1/((Syy*Sy1y1)**0.5)
R2=R*R
print("R2={:.4f}".format(R2))
系数a1=41.5
系数a2=-0.3
截距为=65.3
多元线性回归方程为:y=41.5 X1+ -0.3 X2+65.3
营业额-营业额平均值的和为:-0.0
预测营业额-预测营业额平均值的和为:-0.0
Syy=76199.6
Sy1y1=72026.6
Syy1=72026.6
Se=76199.6
R2=0.9452
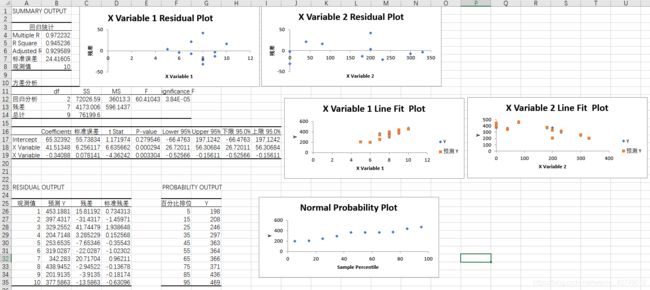
与表格自带的数据分析功能进行比较
四、实验总结
可以看出在最小二乘法和梯度下降法中,最小二乘法在多元情况下计算量偏大,梯度下降法除了迭代次数较多以外计算量其实并不大
关于二者更详细的对比请参见:
线性回归中的最小二乘法和梯度下降法比较