人工智能数学基础之概率论

概率论

基础概率

随机试验

试验是指为了观察某事的结果或某物的性能而从事的某种活动。在概率论中，一个试验如果具有以下3个特点：

1. 可重复性：在相同条件下可以重复进行
2. 可观察性：每次实现的可能结果不止一个，并且能事先明确实验的所有可能结果
3. 不确定性：一次试验之前，不能预知会出现哪一个结果

这样的试验是一个随机试验，简称为试验

样本点和样本空间

每次试验的每一个结果成为基本事件，也称作样本点，记作$w_1,w_2,\cdots$, 全部样本点的集合成为样本空间，记作$\Omega$，则$\Omega =\{w_1,w_2,\cdots \}$

假设掷一颗均匀骰子，观察出现的点数。这是一个随机试验，样本空间$\Omega =\{1,2,3,4,5,6\}$

随机事件

基本事件是不可再分解的、最基本的事件，其他事件均可由它们复合而成，由基本事件复合而成的事件称为随机事件或简称为事件。
常用大写字母$A,B,C$等表示事件。不如$A=\{出现的点数为偶数\}=\{2,4,6\}$

随机事件的概率

概率是用来描述随机事件发生的可能性大小。比如抛硬币的试验，抛得次数越多，出现正面的 次数与投掷次数之间的比例愈加趋于$0.5$。它的数学定义为：

在多次重复试验中，若事件$A$发生的频率稳定在常数$p$附近摆动，且随着试验次数的增加，这种摆动的幅度是很微小的。则称确定常数$p$为事件$A$发生的概率，记作$P(A)=p$

例子
设一年有365天，求下列事件$A,B$的概率：
$$A=\{n个人中没有2人同一天生日\}B=\{n个人中有2人同一天生日\}$$

解
显然事件$A,B$是对立事件，有$P(B)=1-P(A)$
由于每人的生日可能是365天的任意一天，因此，$n$个人的生日有$365^n$种可能结果，而且每种结果是等可能的，因而是古典概型，事件$A$的发生必须是$n$个不同的生日，因而$A$的样本点数为从$365$中取$n$个的排列数$P_{365}^n$，于是

$$\begin{gathered} P(A)=\frac{P_{365}^n}{365^n} \\ P(B)=1-P(A)=1-\frac{P_{365}^n}{365^n} \end{gathered}$$

条件概率

设$A,B$是两个事件，且$P(A)>0$，则称
$$P(B|A)=\frac{P(AB)}{P(A)}$$
为在事件$A$发生的条件下，事件$B$的条件概率
$P(AB)$表示$A,B$这两个事件同时发生的概率。

例子
某种原件用满$6000h$未坏的概率是$3/4$，用满$10000h$未坏的概率是$1/2$，现有一个此种元件，已经用过$6000h$未坏，试求它能用到$10000h$的概率。

解

设$A$表示$\{满10000h未坏\}$,$B$表示$\{满6000小时未坏\}$，则
$$P(B)=3/4,P(A)=1/2$$

由于$B\supset A,AB=A$，因而$P(AB)=1/2$，因此，
$$P(A|B)=\frac{P(AB)}{P(B)}=\frac{\frac{1}{2}}{\frac{3}{4}}=\frac{2}{3}$$

解释一下，这里由于事件$A$包括事件$B$的。

事件的独立性

如果事件$B$发生的可能性不受事件$A$发生与否的影响，即
$$P(B|A)=P(B)$$
则称事件$B$对于事件$A$独立，显然，若$B$对$A$对立，则$A$对$B$也一定独立，称事件$A$与事件$B$相互独立。

例子
口袋里装有5个黑球与3个白球，从中有放回地取2次，每次取一个，设事件$A$表示第一次取到黑球，事件$B$表示第二次取到黑球，则有
$$P(A)=\frac{5}{8},P(B)=\frac{5}{8},P(AB)=\frac{5}{8}\times \frac{5}{8}=\frac{25}{64}$$

因而
$$P(B|A)=\frac{P(AB)}{P(A)}=\frac{5}{8}$$
因此，$P(B|A)=P(B)$，这表明无论$A$是否发生，都对$B$发生的概率无影响。事件$A，B$相互独立

性质

事件$A$和事件$B$相互独立的充分必要条件是
$$P(AB)=P(A)P(B)$$

全概率公式

如果事件$A_1,A_2,\cdots ,A_n$是一个完备事件组(一个事件发生的所有可能性都在这里面)，并且都有正概率，则有
$$P(B)=P(A_1)P(B|A_1)+P(A_2)P(B|A_2)+\cdots +P(A_n)P(B|A_n)=\sum _{i=1}^{n}P(A_i)P(B|A_i)$$

对于任何事件$B$，事件$A\overline{A}$构成最简单的完备事件组，根据全概率公式得
$$P(B)=P(AB+\overline{A}B)=P(AB)+P(\overline{A}B)=P(A)P(B|A)+P(\overline{A})P(B|\overline{A})$$

贝叶斯公式

设事件$A_1,A_2,\cdots ,A_n$是一个完备事件组，则对任一事件$B$，$P(B)>0$，有
$$P(A_i|B)=\frac{P(A_{i}B)}{P(B)}=\frac{P(A_i)P(B|A_i)}{{\sum }_{i=1}^{n}P(A_i)P(B|A_i)}$$

以上公式就叫贝叶斯公式，可由条件概率的定义及全概率公式证明。

例子
市场上供应的某种商品由甲、乙、丙3个厂商生存，甲厂占45%，乙厂占35%，丙厂占20%。如果各厂的次品率依次为4%，2%，5%。现从市场上购买1件这种商品，发现是次品，试判断它是由甲厂生产的概率。

解

设事件$A_1,A_2,A_3$，分别表示商品由甲、乙、丙厂生产的，事件$B$表示商品为次品，得概率
$$\begin{gathered} P(A_1)=0.45,P(A_2)=0.35,P(A_3)=0.20 \\ P(B|A_1)=0.04,P(B|A_2)=0.02,P(B|A_3)=0.05 \end{gathered}$$

根据贝叶斯公式，可得：
$$\begin{gathered} P(A_1|B)=\frac{P(A_{1}B)}{P(B)}=\frac{P(A_1)P(B|A_1)}{P(A_1)P(B|A_1)+P(A_2)P(B|A_2)+P(A_3)P(B|A_3)} \\ =\frac{0.45\times 0.04}{0.45\times 0.04+0.35\times 0.02+0.2\times 0.05}\approx 0.514 \end{gathered}$$

在购买一件商品这个试验中，$P(A_i)$是在试验以前就已经知道的概率，所以习惯地称为先验概率。试验结果出现了次品，这时条件概率$P(A_i|B)$反映了在试验以后对$B$发生的来源(次品的来源)的各种可能性的大小，称为后验概率。

随机变量

把试验的结果与实数对应起来，随试验结果的不同而变化的量就是随机变量，包含离散型随机变量和连续性随机变量。

概率分布

设离散型随机变量$X$的所有可能取值为$x_1,x_2,\cdots ,x_n$，称
$$P\{X=x_k\}=p_k(k=1,2,\cdots )$$
为$X$的概率分布。

离散型随机变量$X$的分布律具有下列基本性质：

1.$p_k\ge 0,K=1,2,\cdots ;$
2.${\sum }_{i=1}^{+\infty }{p}_k=1$

下面看一下常见的离散型概率分布。

二项分布

二项分布是一种离散型的概率分布。二项代表它有两种可能的结果：成功或不成功。每次试验必须相互独立，重复n次，并且每次试验成功的概率是相同的，为$p$：失败的概率也相同，为$1-p$

抛硬币就是一个典型的二项分布。当我们要计算抛硬币$n$次，恰好有$x$次正面朝上的概率，可以使用二项分布的公式：
$$P\{X=k\}=C_n^k{p}^k(1-p{)}^{n-k}$$

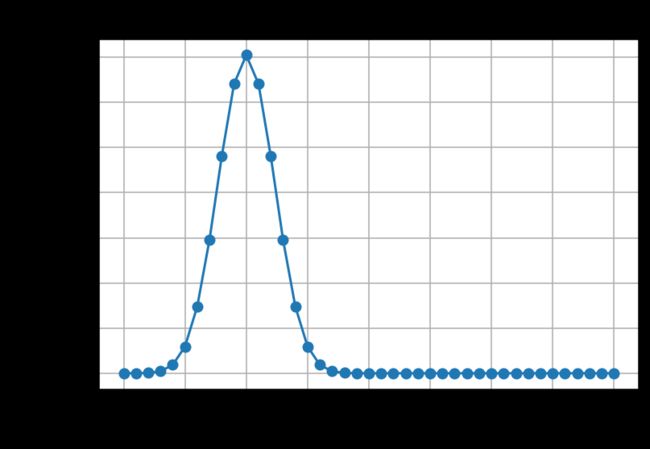
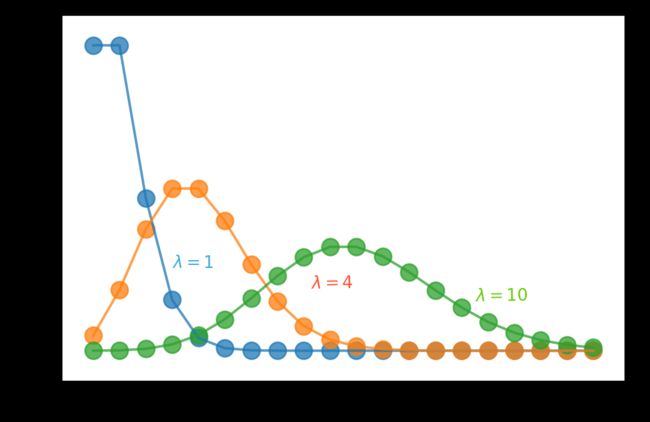
泊松分布

如果随机变量$X$的概率分布为
$$P\{X=k\}=\frac{{\lambda }^k}{k!}{e}^{-\lambda },k=0,1,2,\cdots$$
式中，$\lambda >0$为常数，则称随机变量$X$服从参数为$\lambda$的泊松分布，记为$X\sim P(\lambda )$

概率密度函数

若存在非负函数$f(x)$，使一个连续型随机变量$X$取值于任一区间$(a,b]$的概率可以表示为
$$P\{a<X\le b\}={\int }_a^{b}f(x)d_x$$
则称$f(x)$为随机变量$X$的概率密度函数，简称概率密度或密度函数。

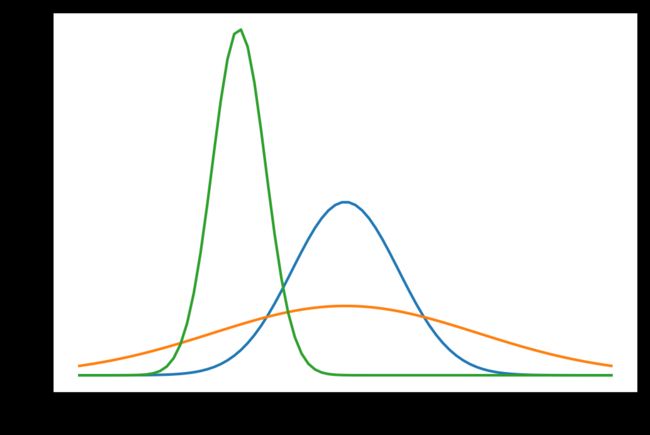
正态分布

又常称为高斯分布，其概率密度函数为
$$f(x)=\frac{1}{\sqrt{2\pi }\sigma }{e}^{-\frac{(x-\mu {)}^2}{2{\sigma }^2}}$$

具有两个参数$\mu$和${\sigma }^2$,$\mu$代表服从正态分布的随机变量的均值，${\sigma }^2$是此随机变量的方差。如果一个随机变量服从均值$\mu$，标准差为$\sigma$的正太分布，记作
$$X\sim N(\mu ,{\sigma }^2)$$

我们通常称均值为$0$，标准差为$1$的正态分布为标准正态分布。

上图中蓝线就是标准正态分布

随机变量的期望

对于一个随机变量，经常要考虑它平均取什么，期望就是概率论中的平均值，对随机变量中心位置的一种度量。

例子

经过长期观察积累，某射手在每次射击命中的环数$X$服从分布：

$X$	0	5	6	7	8	9	10
$P_i$	0	0.05	0.05	0.1	0.1	0.2	0.5

求这个射手平均命中的环数是多少？

解
假设该射手进行了100次射击，那么，约有5次命中5环，5次命中6环，10次命中7环，10次命中8环，20次命中9环，50次命中10环，从而在一次射击中，该射手平均命中的环数为：

$$\frac{1}{100}(10\times 50+9\times 20+8\times 10+7\times 10+6\times 5+5\times 5+0\times 0)=8.85$$

我们可以看到离散型的随机变量的期望值可以用每种取值于概率相乘之和来得到：

$$E(X)=\sum _{i=1}^{+\infty }{x}_i{p}_k$$

期望的性质

1. $E(c)=c$
2. $E(X+c)=E(X)+c$
3. $E(kX)=kE(X)$
4. $E(kX+c)=kE(X)+c$
5. $E(X+Y)=E(X)+E(Y)$

随机变量的方差

方差表示随机变量的变异性，方差越大，随机变量的结果越不稳定。

设$X$为一随机变量，若
$$E[X-E(X){]}^2$$
存在，则称其为$X$的方差，记为$D(X)$，即
$$D(X)=E[X-E(X){]}^2$$
而称$\sqrt{D(X)}$为$X$的标准差或均方差

由方差的定义和数学期望的性质，可以推出方差的计算公式：

$$D(X)=E(X^2)-[E(X){]}^2$$

方差的性质

1. $D(c)=0$
2. $D(X+c)=D(X)$
3. $D(cX)=c^{2}D(X)$

例子

甲、乙两车间生产同一种产品，设1000件产品中的次品数量分别为随机变量$X,Y$，已知他们的分布律如下：

$X$	0	1	2	3
$P_i$	0.2	0.1	0.5	0.2

$Y$	0	1	2	3
$P_i$	0.1	0.3	0.4	0.2

式讨论甲、乙两车间的产品质量。

解

先计算均值
$$\begin{gathered} E(X)=0\times 0.2+1\times 0.1+2\times 0.5+3\times 0.2=1.7 \\ E(Y)=0\times 0.1+1\times 0.3+2\times 0.4+3\times 0.2=1.7 \end{gathered}$$

得到，甲、乙两车间次品数的均值相同。

再计算方差
$$\begin{gathered} D(X)=(0-1.7{)}^2\times 0.2+(1-1.7{)}^2\times 0.1+(2-1.7{)}^2\times 0.1+(2-1.7{)}^2\times 0.5+(3-1.7{)}^2\times 0.2=1.01 \\ D(Y)=(0-1.7{)}^2\times 0.1+(1-1.7{)}^2\times 0.3+(2-1.7{)}^2\times 0.4+(2-1.7{)}^2\times 0.4+(3-1.7{)}^2\times 0.2=0.81 \end{gathered}$$

以上用到了公式$E(X)={\sum }_{i=1}^{+\infty }{x}_i{p}_k$和$D(X)=E[X-E(X){]}^2$

说明乙车间的产品质量比较稳定。

最大似然估计

概率vs统计

概率研究的问题是，已知一个模型和参数，怎么去预测这个模型产生的结果的特性（均值，方差等）。统计研究的问题则相反，它是有一堆数据，要利用这堆数据去预测模型和参数。简单来说，概率是已知模型和参数，推数据。统计是已知数据，推模型和参数。

最大似然估计

最大似然估计是一种用来推测参数的方法，属于统计领域的问题。
它利用已知的样本结果信息，反推使这个结果出现可能性最大的模型参数值，是一种概率意义下的参数估计。

例子

假设有一种特殊的硬币，抛这种硬币出现的正反面并不相等，求它正面出现的概率($\theta$)是多少？

解
这是一个统计问题，解决统计问题需要数据。于是我们拿这枚硬币抛了10次，得到的数据$x_0$是：反正正正正反正正正反。我们相求的正面概率$\theta$是模型参数，而抛硬币模型我们可以假设是二项分布。那么出现实验结果$x_0$的似然函数是多少呢？

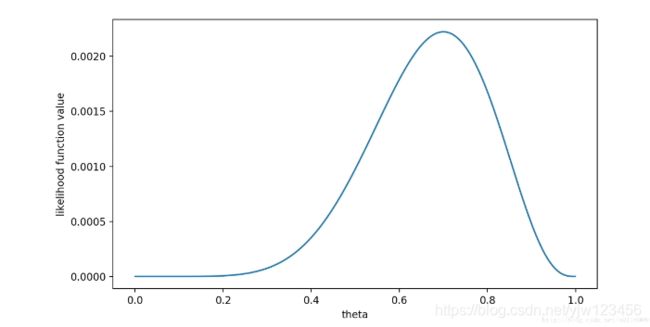
$$f(x_0,\theta )=(1-\theta )\times \theta \times \theta \times \theta \times \theta \times (1-\theta )\times \theta \times \theta \times \theta \times (1-\theta )={\theta }^7(1-\theta {)}^3=f(\theta )$$

所谓最大似然估计，就是最大化这个关于$\theta$的函数，于是，我们画出$f(\theta )$的图像:

可以看出，在$\theta =0.7$时，$f(\theta )$取得最大值。

这样，我们已经完成了对$\theta$的最大似然估计。即，抛10次硬币，发现7次硬币正面朝上，最大似然估计认为正面朝上的概率是0.7。

参考

1. 微专业人工智能机器学习数学高等数学概率论统计学基础进阶课程（完整版）