计算机数据表示方法及工业标准IEEE754讲解教程
本文主要对计算机系统中数据的表示形式及工业IEEE754标准进行讲解,如有不当,敬请提出修改,敬请阅读!
目录
原码表示法
反码表示法
补码表示法
移码表示法
定点数
浮点数
工业标准IEEE754
Hello!你好呀,我是灰小猿!一个超会写Bug的沙雕程序猿!
今天在这里和大家记录一下在计算机系统中各种数据的表示方式以及工业标准IEEE754的使用方法。
首先了解一个概念:
各种数据在计算机中表示的形式称为机器数,其特点是数的符号用二进制数0、1表示。机器数对应的实际数值称为该数的真值。与此同时,机器数又分为无符号数和带符号数两种。无符号数表示正数,在机器数中没有符号位。对于带符号数,机器数的最高位是表示正、负的符号位,其余二进制位表示数值。带符号的机器数可采用原码、反码、补码和移码等编码方法。机器数的这些编码方法称为码制。
接下来分别对这几个编码方式的使用讲解。
原码表示法
在原码表示中,数值X的原码记为[X]原,如果机器字长为n(也就是用n个二进制数表示),则原码的定义如下:
注意:上述公式中的范围之所以到2的n-1次方,是因为该二进制数的第一位表示正负,这就导致了大于等于2的7次方的数都无法表示。
例如当机器字长n等于8时,下列各数的原码为:
注意:小数用二进制数表示时,小数点后第一位表示2的-1次方,第二位表示2的-2次方......以此类推。
机器数的最高位是符号位,0代表正号,1代表负号,余下各位是数的绝对值。零有两个编码,即:
原码表示方法的优点在于数的真值和它的原码表示之间的对应关系简单,相互转换容易,用原码实现乘除运算的规则简单;
缺点是用原码实现加减运算很不方便。
反码表示法
在反码表示中,数值X的反码记为[X]反,如果机器字长为n,则反码的定义如下:
例如当机器字长n等于8时,下列各数的反码为:
机器数的最高位是符号位,0代表正号,1代表负号。
当符号位为0时,其余几位即为此数的二进制值;
但当符号位为1时,则要把其余几位按位取反,才是它的二进制值。
零有两个编码,即:
补码表示法
在补码表示中,数值X的补码记为[X]补,如果机器字长为n,则补码的定义如下:
例如当机器字长n等于8时,下列各数的补码为:
机器数的最高位是符号位,0代表正号,1代表负号。
当符号位为0(即正数)时,其余几位即为此数的二进制值;
但当符号位为1(即负数)时,其余几位不是此数的二进制值,需把它们按位取反,且最低位加1,才是它的二进制值。
零有唯一的编码, 即
补码表示的两个数在进行加法运算时,只要结果不超出机器所能表示的数值范围,可以把符号位与数值位同等处理,运算后的结果按2取模后,得到的新结果就是本次加法运算的结果。
移码表示法
移码表示法是在数X上增加一个偏移量来定义的,常用于表示浮点数中的阶码。如果机器字长为n,规定偏移量为2的n-1次方,则移码定义为:
例如当机器字长n等于8时,下列各数的原码为:
在偏和量为2的n-1次方的情况下,只需要将补码的符号位取反就可以得到相应的移码表示。
除了以上原码、补码这些数据表示方法以外,在计算机中的数据表示还有定点数和浮点数两种,
定点数
所谓定点数,就是小数点的位置固定不变的数。小数点的位置通常有两种约定方式,分别是:
定点整数(纯整数,小数点在最低有效数值位之后)
定点小数(纯小数,小数点在最高有效数值位之前)
浮点数
所谓浮点数,就是小数点位置不固定的数,它能表示更大范围的数值,
先来看一个例子,当机器字长为n时,定点数的补码和移码可表示个数,而其原码和反码只能表示个数,因为在原码和反码中0的表示占用了两个编码,因此定点数所能表示的数值范围比较小,在运算中容易因为结果超出范围而溢出,但是由于浮点数是小数点位置不固定的数,因此它能表示更大的数。
浮点数通常的表示方法是:
![]()
其中M为尾数,R为基数(一般为2),E为阶码,
因此如果想要表示一个浮点数,就必须要给出尾数M,它决定了浮点数的表示精度,同时要给出阶码E,它指出了小数点在数据中的位置,也决定了浮点数的表示范围,这种方法表示的数称为浮点数,这种表示数的方法也被称为浮点表示法。
在浮点表示法中,码阶为带符号的纯整数,尾数为带符号的纯小数,浮点数的表示格式如图所示:
| 阶符 |
码阶 |
数符 |
尾数 |
从上面我们就可以看出,一个数的浮点表示不是唯一的,当小数点的位置改变时,阶码也随之相应的改变,因此可以用多个浮点形式表示同一个数,
浮点数所能表示的数值范围主要由阶码决定,所表示数值的精度则由尾数决定。为了充分利用尾数来表示更多的有效数字,通常采用规格化浮点数。规格化就是将尾数的绝对值限定在区间[0.5, 1]。
当尾数用补码表示时,需要注意如下问题:
①若尾数M≥0,则其规格化的尾数形式为M=0.1XXX...X,其中,X可为0,也可为1,即将尾数限定在区间[0.5, 1]。
②若尾数M<0,则其规格化的尾数形式为M=1.0XXX...X,其中,X可为0,也可为1,即将尾数M的范围限定在区间[-1, -0.5]。
如果浮点数的阶码(包括1位阶符)用R位的移码表示,尾数(包括1位数符)用M位的补码表示,则这种浮点数所能表示的数值范围如下:
注意:若表示范围超过了计算机的表达范围,就称为溢出。
工业标准IEEE754
工业标准IEEE754是由IEEE制定的有关浮点数的工业标准,该标准目前被广泛采用,该标准的表示形式如下:
其中,为该数的数符,当S为0时表示正数,当S为1时表示负数,E为指数(阶码)用移码表示,为尾数,其长度为P位,用原码表示,
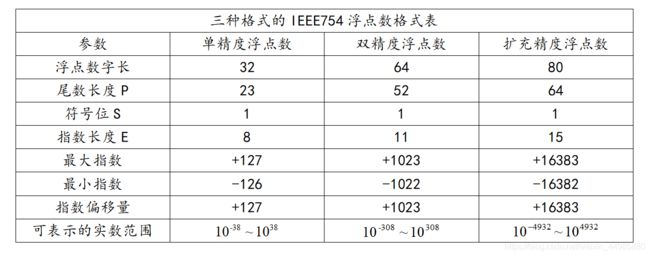
计算机中主要使用三种形式的IEEE754浮点数,分别是:单精度浮点数、双精度浮点数、扩充精度浮点数,下表为三种格式的IEEE754浮点数格式表。
关于数据在计算机中的表示方法就先暂且先总结到这里了,之后还会继续更新完善。
觉得不错记得点赞关注哟!
大灰狼陪你一起进步!