ANDROID高级UI-贝塞尔曲线PATH

认识贝塞尔曲线

贝塞尔曲线分类：

• 一阶贝塞尔
  

简单粗暴点就是绘画开始的第一个控制点计算起，图中P1为第一个控制点就称之为一阶贝塞尔。

• 二阶贝塞尔

从绘画开始的第一个控制点计算起，P1为第一个，P2为第二个，总共为二个，就称之为二阶贝塞尔曲线。

• 三阶与N阶贝塞尔
  

从图中可以看出最顶端两个点，以及右下角的一个控制点，通过这些控制点连接起来构成一个三阶贝塞尔曲线。 N阶曲线以此类推。计算公式可从网上查找。

• 四阶贝塞尔
  
• 五阶贝塞尔
  

从上边看下来，记住一句话，从第一个控制点数起，有几个控制点就是就是几阶，以此类推。

对贝塞尔有一点了解就可以，那么怎么绘画呢？就涉及到Path这个类了，如果想彻底掌握贝塞尔，就要对Path一个全新的认知和理解，下来进入对Pah的详解。

PathAPI

• 首先我写了一个自定义View继承View

public class PathView extends View {
private Path mPath1=new Path();
private Path mPath2=new Path();
private Paint mPaint=new Paint();

public PathView(Context context) {
    super(context);
    mPaint.setColor(Color.RED);
    mPaint.setStrokeWidth(4);
    mPaint.setStyle(Paint.Style.STROKE);
    }
}

mPaint.setColor(Color.RED); 设置画笔的颜色
mPaint.setStrokeWidth(4); 设置画笔的宽度
mPaint.setStyle(Paint.Style.STROKE);画笔的样式
Paint.Style
STROKE 描边
FILL 填充
FILL_AND_STROKE 描边以及填充区域

onDraw方法

@Override
protected void onDraw(Canvas canvas) {
    super.onDraw(canvas);

    //添加圆
    mPath1.addCircle(200,200,100,Path.Direction.CW);
    canvas.drawPath(mPath2,mPaint);
}

mPath1.addCircle(200,200,100,Path.Direction.CW);
addCircle 添加一个圆
addCircle(float x, float y, float radius, Direction dir)
float x X坐标
float y y坐标
float radius 圆的半径
Path.Direction 绘制方向
Path.Direction.CW 顺时针
Path.Direction.CCW 逆时针

• float x float y
  

• addCircle
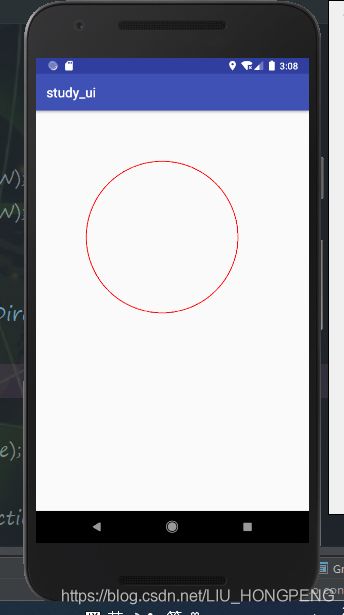
  void addCircle(float x, float y, float radius, Direction dir)

  mPath1.addCircle(500,500,300,Path.Direction.CW);

  添加圆形，x坐标越大，圆形离左边距离越大，y坐标越大，圆离上边距离越大，Direction 绘制方向是顺时，还是逆行。
  

• addArc
  void addArc(float left, float top, float right, float bottom, float startAngle,float sweepAngle)

  mPath1.addArc(200, 200, 300, 300, 0, -90);

  添加椭圆弧线，
  float left, float top, float right, float bottom
  矩形由4个点组成（left，top， right， bottom）
  left矩形左距离，
  top 矩形左上角离屏幕上边的距离，
  right 矩形 右上角离屏幕的右边距离，
  bottom 矩形 右下角离屏幕上边的距离
  startAngle 圆弧起始 角度 3点钟方向为0度
  sweepAngle 圆弧扫描度数

  效果图
  
  矩形坐标参考文章

  矩形坐标，left, top, right, bottom

  圆角弧度坐标参考文章

  圆角弧度坐标 startAngle , sweepAngle

• arcTo
  arcTo(float left, float top, float right, float bottom, float startAngle, float sweepAngle, boolean forceMoveTo)

  mPath1.arcTo(0, 50, 800, 100, 0, 180, true);

  添加路径
  参数如椭圆弧线差不多，唯一多了个参数
  boolean forceMoveTo

  简单粗暴点理解就是需不需要在上个画面接着开始绘制，false代表在原有的上边开始，ture就是不陪你玩了，自立门户。

  boolean forceMoveTo
  false效果图
  
  boolean forceMoveTo
  true效果图
  

• addOval
  void addOval(float left, float top, float right, float bottom, Direction dir)
  mPath1.addOval(300, 300, 400, 450, Path.Direction.CW);

  添加椭圆

  效果图
  

• addRect
  void addRect(float left, float top, float right, float bottom, Direction dir)

  mPath1.addRect(100,400,300,500, Path.Direction.CW);

  添加矩形
  效果图
  

• addRoundRect
  void addRoundRect(float left, float top, float right, float bottom, float rx, float ry，irection dir)

  mPath1.addRoundRect(100,600,300,700,20,40, Path.Direction.CW);

  添加圆形矩形
  效果图
  

• op
  boolean op(Path path, Op op)

op参数
Path.Op.INTERSECT 保留公共部分
Path.Op.DIFFERENCE 减去两个路径的交叉
Path.Op.UNION 与DIFFERENCE 一样
Path.Op.XOR 与原图一样没什么变化

先看一个
Path.Op.INTERSECT 保留公共部分

mPath1.addCircle(200,200,100,Path.Direction.CW);
mPath2.addCircle(300,300,100,Path.Direction.CW);

mPath1.op(mPath2, Path.Op.INTERSECT);

canvas.drawPath(mPath1,mPaint);
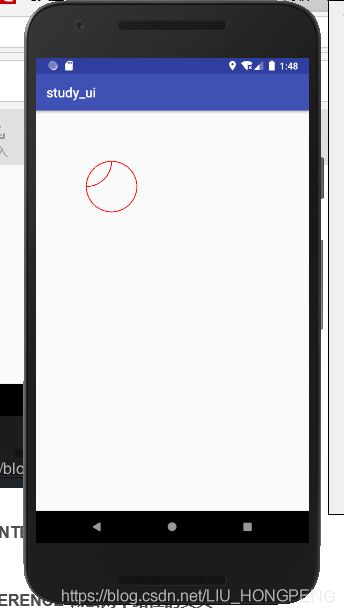
canvas.drawPath(mPath2,mPaint);

未调用Path.Op.INTERSECT方法，效果图：

调用Path.Op.INTERSECT 之后效果图

第二个参数
Path.Op.DIFFERENCE 减去两个路径的交叉

mPath1.addCircle(200,200,100,Path.Direction.CW);
mPath2.addCircle(300,300,100,Path.Direction.CW);
//------------------
mPath1.op(mPath2, Path.Op.DIFFERENCE);

canvas.drawPath(mPath1,mPaint);
canvas.drawPath(mPath2,mPaint);

未调用Path.Op.DIFFERENCE效果图

调用Path.Op.DIFFERENCE之后效果图

第三个参数
Path.Op.UNION 与DIFFERENCE 一样，减去交叉部分

mPath1.addCircle(200,200,100,Path.Direction.CW);
mPath2.addCircle(300,300,100,Path.Direction.CW);

mPath1.op(mPath2, Path.Op.UNION);

canvas.drawPath(mPath1,mPaint);
canvas.drawPath(mPath2,mPaint);

Path.Op.UNION 效果图

第三个参数
Path.Op.XOR，没什么变化

mPath1.addCircle(200,200,100,Path.Direction.CW);
mPath2.addCircle(300,300,100,Path.Direction.CW);

mPath1.op(mPath2, Path.Op.XOR);

canvas.drawPath(mPath1,mPaint);
canvas.drawPath(mPath2,mPaint);

Path.Op.XOR 效果图

• lineTo
  void lineTo(float x, float y)
  绘制一条直线

在网上查不到好的结果，大部分抄袭比较多，个人经过多次运行验证，
float x x坐标
float y y坐标
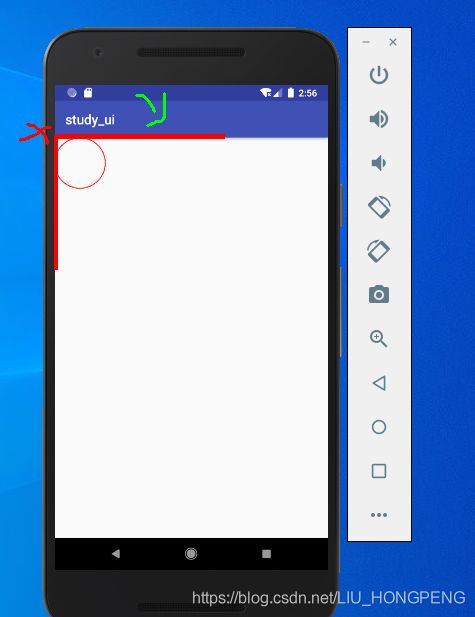
绘制线的位置是从0,0坐标绘制的，x坐标相当于0到屏幕左边的位置，
y坐标相当于0到线下边的距离，有图有真相。

mPath1.lineTo(400,400);

canvas.drawPath(mPath1, mPaint);

实际图

当x值加大时，横线的距离里左边越大。

mPath1.lineTo(700,400);//加大300

x值加大300效果图

当y值加大时，垂直的距离里越大。

mPath1.lineTo(400,700);

y值加大300效果图

最终就得到400x700一条直线：

• moveTo
  void moveTo(float x, float y)
  看字面意思就是移动到某个位置的意思。

float x, float y
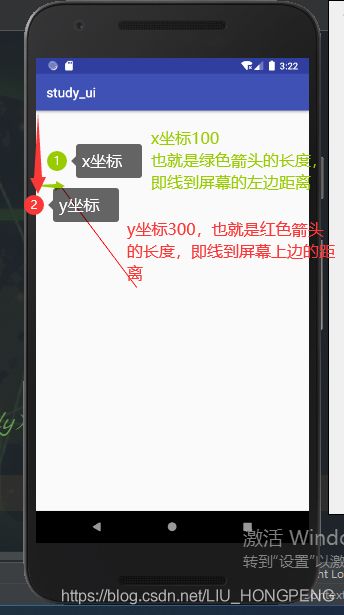
float x x坐标计算上边已经讲过了，唯一区别不同的是这里的
x坐标是移动（0,0）开始绘制的x坐标，y坐标。
移动直线的x坐标，也就是绘制开始位置的x坐标
float y
移动直线的y坐标，也就是绘制开始位置的y坐标。

mPath1.moveTo(100,300);
mPath1.lineTo(400,700);

canvas.drawPath(mPath1, mPaint);

移动x坐标100，y坐标300位置图

• rMoveTo
  void rMoveTo(float dx, float dy)
  移动画笔位置，类似moveTo

与moveTo一样，移动画笔位置。
唯一区别在前一个点的基础上开始绘制，
如果前面一个点是（x,y）rMoveTo（dx,dy）
相当于moveTo（x+dx,y+dy）
如果前面没有调用moveTo 相当于从（dx,dy）开始绘制

什么意思呢？画一张图理解更加深刻。

mPath1.moveTo(100,200);
mPath1.rMoveTo(100,100);
mPath1.lineTo(400,700);
canvas.drawPath(mPath1, mPaint);

从代码看出，在rMoveTo之前调用了moveTo，
那么最终坐标就是 x100+rx100=x200，y200+100=y300,
即结果 x200,y300
注释：
lineTo的坐标与其他坐标无关，它的坐标是线的坐标，而moveTo以及rMoveTo是移动画笔绘画开始的坐标。

rMoveTo之前调用moveTo效果图

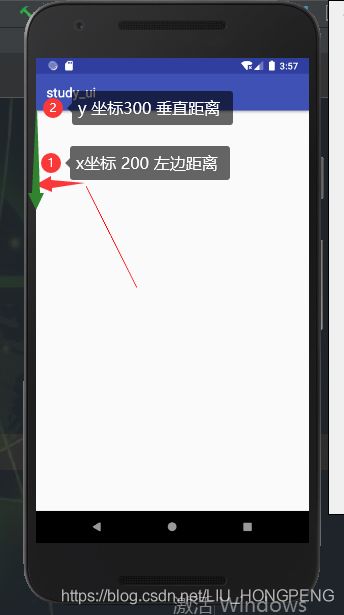
rMoveTo之前未调用任何移动坐标点方法效果图

mPath1.rMoveTo(100,100);

• close
  void close()
  闭合

闭合
什么意思呢？两根线，把第一根线的线头，和第二根的线尾结合起来。

mPath1.rLineTo(100,300);
mPath1.lineTo(400,700);
mPath1.close();
canvas.drawPath(mPath1, mPaint);

未调用close效果图

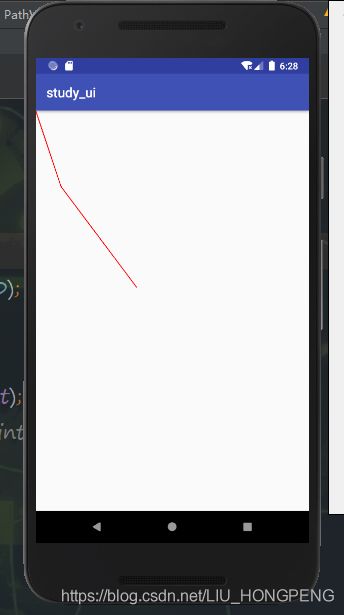
调用close效果图

相信从上边相信看下来，应该对这些常用的api有点认识了，对x,y坐标有一定了解了，接下来就练练手，绘制一根二阶贝塞尔曲线。

• quadTo
  void quadTo(float x1, float y1, float x2, float y2)

这是翻译后的大概意思，
从最后一个点开始添加一个二次贝塞尔函数，接近控制点（x1,y1),结束于（x2，y2）。如果未对此等高线执行moveTo（）调用，则第一个点将自动设置为（0,0）.
float x1 控制点x坐标
float y1 控制点y坐标
float x2 终点x坐标
float y2 终点y坐标

quadTo效果图

quadTo绘画流程参考以下文章

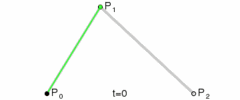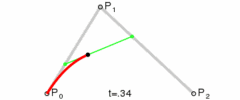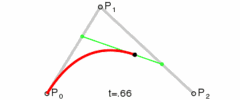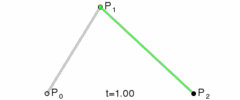
二阶贝塞尔曲线绘画流程参考

绘画过程参考效果

• cubicTo
  void cubicTo(float x1, float y1, float x2, float y2,
  float x3, float y3)

  三阶贝塞尔曲线

  唯一区别：比二阶贝塞尔曲线多了一个控制点。

     mPath1.moveTo(100,100);
     mPath1.cubicTo(400,200,10,500,300,700);

float x1,第一个控制点坐标x
float y1,第一个控制点坐标y
float x2, 第二个控制点坐标x
float y2, 第二个控制点坐标y
float x3, 第三个控制点坐标x
float y3 第三个控制点坐标y

cubicTo效果图

作品效果图，附资料供参考与学习：

qq气泡

另附一阶贝塞尔曲线到十阶以上贝塞尔贝塞尔公式算法以及会三角算法两种算法。

资料下载移步：
资料参考下载