C++搜索算法和曼哈顿距离之最少连通代价

最少联通代价

Description

在一个N行M列的字符网格上，恰好有 2 个彼此分开的连通块。每个连通 块的一个格点与它的上、下、左、右的格子连通。如下图所示：

现在要把这 2 个连通块连通，求最少需要把几个’.’转变成’X’。上图的例子中， 最少只需要把 3 个’.’转变成’X’。下图用’*’表示转化为’X’的格点。

Input

第1行：2个整数N和M(1<=N,M<=50)接下来 N 行，每行M个字符，’X’表示属于某个连通块的格点，’.’表示不属于某个连通块的格点。

Output

第1行：1个整数，表示最少需要把几个’.’转变成’X’。

Sample Input

6 16            
................
..XXXX....XXX...
...XXXX....XX...
.XXXX......XXX..
........XXXXX...
.........XXX....

Sample Output

3

Hint

1<=N,M<=50

解题

方法一: 深搜+广搜

这道题可以先用深搜把第一个连通块的的格点改为'S'，然后广搜从每个'S'到某个'X'的最短距离(即到第二个连通块的最短路线长度)，在这些结果里找到最小的，最后输出。

代码如下:

#include
#include
#include
using namespace std;
int n,m;
int pre[1000000],a[1000000],b[1000000]; //pre用于存储广搜时的前驱，a、b用于存储位置
int minn,ans=1e10; //minn用与存储每次广搜的值，ans用于取最小值
int x[4]={1,-1,0,0},y[4]={0,0,1,-1}; //方向
char map[100][100]; //用于记录字符网格
bool mark[100][100]; //记录当前格点是否走过
bool check(int s,int t) //判断是否可以走到下一个格点
{
	if(s&&t&&s<=n&&t<=m&&!mark[s][t]&&map[s][t]!='S') return 1;
	return 0;
}
void fun(int d) //根据前驱来计算距离
{
	minn++;
	if(pre[d]) fun(pre[d]);
}
void bfs(int r,int c) //计算到第二个连通块的最短距离仔细写
{
	memset(mark,0,sizeof(mark)); //清零，以便广搜
	minn=0; //清零，以便计数
	int head=0,tail=1;
	int nextr,nextc;
	mark[r][c]=1; //标记初始位置
	pre[1]=0; //设置前驱
	a[1]=r;
	b[1]=c;
	while(head!=tail)
	{
		head++;
		for(int i=0;i<4;i++)
		{
			nextr=a[head]+x[i];
			nextc=b[head]+y[i];
			if(check(nextr,nextc))
			{
				tail++;
				a[tail]=nextr;
				b[tail]=nextc;
				mark[nextr][nextc]=1;
				pre[tail]=head;
				if(map[nextr][nextc]=='X')
				{
					fun(tail);
					ans=min(minn,ans);
				}
			}
		}
	}
}
void dfs(int r,int c) //将第一个连通块的所有格点改为'S'
{
	for(int i=0;i<4;i++)
		if(check(r+x[i],c+y[i])&&map[r+x[i]][c+y[i]]!='.') //判断能否对其进行"改造"
		{
			map[r+x[i]][c+y[i]]='S'; //"改造"
			dfs(r+x[i],c+y[i]);
		}
}
void f() //将第一个连通块的所有格点改为'S'
{
	for(int i=1;i<=n;i++)
		for(int j=1;j<=m;j++)
			if(map[i][j]=='X')
			{
				dfs(i,j);
				map[i][j]='S'; //将当前位置改为'S'
				return ; //结束函数，以免把第二个连通块也改为'S'
			}
}
int main()
{
	scanf("%d%d",&n,&m);
	for(int i=1;i<=n;i++)
		scanf("%s",map[i]+1);
	bool flag=1;
	f(); //将第一个连通块的所有格点改为'S'
	for(int i=1;i<=n;i++)
		for(int j=1;j<=m;j++)
			if(map[i][j]=='S')
				bfs(i,j); //计算到第二个连通块的最短距离
	printf("%d",ans-2); //-2是因为要删去起点、终点
}

方法二: 深搜+曼哈顿距离

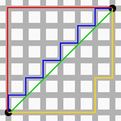
先用深搜把第一个连通块的的所有格点改为'S'，再求曼哈顿距离(如图)。

                             

代码如下:

#include
#include
#include
#include
using namespace std;
int n,m;
int ans=1e10; //ans用于取最小值
int x[4]={1,-1,0,0},y[4]={0,0,1,-1}; //方向
char map[100][100]; //用于记录字符网格
bool check(int s,int t) //判断是否可以走到下一个格点
{
	if(s&&t&&s<=n&&t<=m&&map[s][t]!='S') return 1;
	return 0;
}
void dfs(int r,int c) //将第一个连通块的所有格点改为'S'
{
	for(int i=0;i<4;i++)
		if(check(r+x[i],c+y[i])&&map[r+x[i]][c+y[i]]!='.') //判断能否对其进行"改造"
		{
			map[r+x[i]][c+y[i]]='S'; //"改造"
			dfs(r+x[i],c+y[i]);
		}
}
void f() //将第一个连通块的所有格点改为'S'
{
	for(int i=1;i<=n;i++)
		for(int j=1;j<=m;j++)
			if(map[i][j]=='X')
			{
				dfs(i,j);
				map[i][j]='S'; //将当前位置改为'S'
				return ; //结束函数，以免把第二个连通块也改为'S'
			}
}
int main()
{
	scanf("%d%d",&n,&m);
	for(int i=1;i<=n;i++)
		scanf("%s",map[i]+1);
	bool flag=1;
	f(); //将第一个连通块的所有格点改为'S'
	for(int i=1;i<=n;i++)
		for(int j=1;j<=m;j++)
			for(int k=1;k<=n;k++)
				for(int h=1;h<=m;h++)
					if(map[i][j]=='S'&&map[k][h]=='X')
						ans=min(ans,abs(i-k)+abs(j-h)-1); //运用曼哈顿距离，因重复删去1
	printf("%d",ans);
}