Propensity Score Matching
- Propensity Score Matching 倾向性得分匹配
- 直观解释
- 引言
- Randomized Controlled Trials Vs Observational Studies
- The Potential Outcomes Framework and Average Treatment Effects
- RCTs
- Observational Studies
- Propensity Score Matching
- 参考资料
Propensity Score Matching 倾向性得分匹配
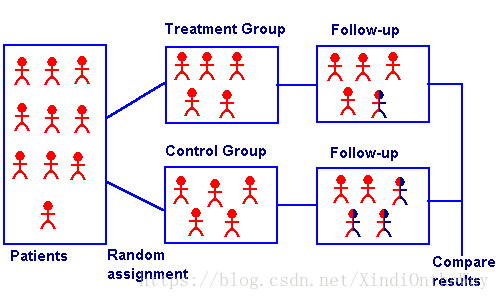
Propensity Score Matching is a technique that attempts to simulate the random assignment of treatment and control groups by matching treated subjects to untreated subjects that were similarly likely in the same group.
倾向性得分匹配是一种根据观测数据模拟随机分配实验组(treatment group)和对照组(control group)的技术。基本方法是将实验组的subject和对照组那些和该subject有相同可能性接受treatment的subject相匹配,从而使得实验组和对照组有着相似的observed baseline covariates分布。
直观解释
想研究A这个人上研究生对他收入的影响,本应该用Y1(上了研究生后的收入)—Y0(如果他不上研究生,他的收入)。正因为Y0是反事实(counterfactual)的,所以要找个对照组。如果Z是影响他选择上不上研究生的变量,假设如果用logit模型估计出了他上研究生的概率为0.8,而B这个人没有上研究生,B的概率刚好也是0.8,所以我们就选择B这个人作为A的对照组。
引言
Randomized controlled trials (RCTs)是估计治疗(treatment),干预(intervention)以及exposure对于结果影响的黄金准则。受试者是否接受treatment完全随机,这就保证了受试的状态不受任何观测到或者未观测到的baseline characteristics的影响。因此,treatment effect可以通过直接比较实验组和对照组的结果获得。
但很多时候实验成本很高或者很难做实验,越来越多的人开始研究如何直接从观测到的数据来衡量treatment effects on outcomes。但是在观测数据中,是否接受treatment一般是受subject characteristic影响的,这就使得treated subjects和untreated subjects通常在baseline characteristic上会显示系统性的区别。Propensity Score Matching就是一种通过观测数据模拟随机实验来衡量treatment outcome的方法。
Randomized Controlled Trials Vs Observational Studies
The Potential Outcomes Framework and Average Treatment Effects
在Potential Outcomes Framework中,我们有两种treatment状态(active treatment和controlled treatment,也即受试和不受试)和一个结果(outcome)。给定一组subjects和一种treatment,每个subject有一对potential outcomes: Yi(0) Y i ( 0 ) (不接受treatment的结果)和 Yi(1) Y i ( 1 ) (接受treatment的结果),如果我们用 Zi Z i 来指示 Xi X i 是否接受treatment,对于每个subject, Zi Z i 要么等于1,要么等于0,也就是说对于每个subject我们只能观测到一种结果:
Treatment Effect定义为:
Average Treatment Effect(ATE)定义为:
Average Treatment Effect for the Treated(ATT):
在RCT中,ATE和ATT是一样的,因为分配的随机性,平均来看,受试人群并不会与总体产生系统上的偏差。
RCTs
在RCTs中,是否受试完全是随机的,因此
Observational Studies
而在观测性研究中,assignment of treatment and control groups并不是随机的, E(Y(1)|Z=1)≠E(Y(1)) E ( Y ( 1 ) | Z = 1 ) ≠ E ( Y ( 1 ) ) ,因此
Propensity Score Matching
The propensity score was defined by Rosenbaum and Rubin (1983a) to be the probability of treatment assignment conditional on observed baseline covariates: ei=Pr(Zi=1|Xi) e i = P r ( Z i = 1 | X i ) .
倾向性得分是基于观测到的受试者的特征,该受试者被分到实验组的概率
在实际中,propensity score通常使用logistic回归模型来估计,即以观测到的baseline charateristics为x,是否接受treatment为y,通过在训练集上拟合可以得到subject接受treatment的概率。Propensity Score Matching就是将观测数据进行重新划分,使得treated sets和untreated sets有相似的propensity score。最常用的匹配方法是one-to-one匹配。
一旦形成matched sample,我们就可以直接比较treated group和control group来衡量treatment effect了。
参考资料
An Introduction to Propensity Score Methods for Reducing the Effects of Confounding in Observational Studies
What is a Propensity Score