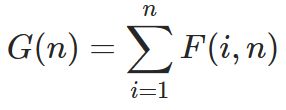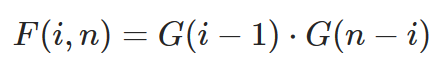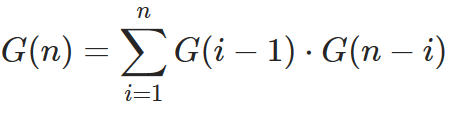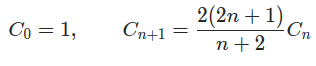【编程学习笔记】动态规划的核心——状态转移方程（递归方程）

在上一章中讲了基本的动态规划思路，但上一章中的状态转移（即小问题之间的关系）过于简单。

（上一章：https://blog.csdn.net/qq_42152365/article/details/107304816）

今天来看一道经典题：

动态规划，首先考虑状态是什么（“小问题”）以及状态之间的关系：

假设我们一共有6个数[1,2,3,4,5,6]，现在已经写好了一个父节点4，手里还有几个数[1,2,3,5,6]，根据二叉搜索树的定义，我要把[1,2,3]挂在左子树，[5,6]挂在右子树上。我们再考虑左子树，[1,2,3]均可以作为父节点，确定了一个父节点后，剩下的又是“确定父节点，且手里还有几个数”的问题。这样看来，状态应该是“确定父节点，手里还有数，有多少种组合方案”

但是这样一来，会出现一些问题，第一，我们的大问题是不确定父节点的，所以需要一个大循环。第二，更关键的是，我们难以存储“以某个父节点和剩下的若干个数为手头的数有多少种可能性”作为记录。（你可以试着按上面的思路写一段dp函数）

现在再来思考一下，“[1,2,3]挂在左子树，[5,6]挂在右子树上”这句话，事实上，[5,6]挂在子树上和[1,2]挂在子树上对于程序来说并没有任何区别，这就非常方便记录，而我们的大问题，恰好就是把[1,2,3...n]挂在一棵树上！那么我们是否有可能把状态确定为“把[1,2,3...n]挂在树上有几种可能”呢？

假设，这个状态为G(n)

显然：

（感谢LeetCode提供的公式图）

其中F(i,n)表示“以i为父节点，剩下数为手头的数有多少种可能性”，而F(i,n)中，1~(i-1)构成的子树数量就是G(i-1)，(i+1)~n构成的子树数量就是G(n-i)，仔细思考这个地方！这里就是状态转移的关键！

那么对于F(i,n)而言，总子树可能性，就应该等于左右子树数量的乘积：

就得到：

这就是本题的状态转移方程，是不是比上一章中的要复杂一些了。

有了这个状态转移方程，dp就非常清晰了。

当然，还有一个问题，dp的最小问题是啥？也就是说递归的出口在哪里？

显然，递归的出口在G(0)和G(1)也就是当我们手里没有数或者只有一个数的时候，就只能构成1个子树(注意，空树也算是1，不是0，如果算成0的话乘一下就全成0了！)，当然，你也可以把G(2)、G(3)这些也算上。

class Solution {
public:
    int G_list[99];
    int dp(int n){
        if(n==0 || n==1){return 1;}
        if(G_list[n]!=0){
            return G_list[n];
        }
        for(int i=1;i<=n;i++){
            G_list[n]+=dp(i-1)*dp(n-i);
        }
        return G_list[n];
    }
    int numTrees(int n) {
        return dp(n);
    }
};

是不是感觉找对了转移方程就简单的一匹？

LeetCode官方提供的非递归解（算法是一样的）：

    int numTrees(int n) {
        vector G(n + 1, 0);
        G[0] = 1;G[1] = 1;
        for (int i = 2; i <= n; ++i) {
            for (int j = 1; j <= i; ++j) {G[i] += G[j - 1] * G[i - j];}
        }
        return G[n];
    }

G(n)在数学上被称为“Catalan”数列，其递推公式为：

所以更加优化的算法如下（状态是Cn，状态转移方程就是Catalan的递推公式）：

    int numTrees(int n) {
        long long int res = 1;
        for(int i=0;i

可见，状态转移方程对dp来说是极其重要的！