datawhale八月组队学习--LeetCode刷题(siguo)

本次加入datawhale组织的八月份组队学习,选择了力扣刷题的小组,刷点题目,让自己的脑子不那么僵化
力扣链接https://leetcode-cn.com/

---

50.pow(x,n)

题目描述：实现 pow(x, n) ，即计算 x 的 n 次幂函数。
还未开始看题,看到题目的时候，心里想着或许是刚开始学习,先拿点简单的练手,当看到困难评级为中等的时候,突然意识到事情不对。

• 题目的描述很简单,计算幂函数，不过重点肯定不是粗暴的计算,而是通过内存与时间的限制,取得AC。
• 说明中的数值范围给得挺大的,暴力计算势必会导致时间超限。
• 毕竟是刷题,肯定还是自己计算,而不是调包求解,不然就没有意义了。

---

尝试解题

• 递归方法（失败）：尝试使用递归方法,空间换时间,不过因为递归层数太多了,在极限的测试用例下直接报错。
• 改进方法（成功）：既然递归深度太深,那就想办法减小递归的深度,经过半个多小时的冥思苦想,对原本的递归方法进行改进,终于成功AC。
• 

double myPow(double x, int n)
{
	if (n == 0)
		return 1;
	if (n > 0)
	{
		if (n % 2 == 1)
			return x * myPow(x*x, n / 2);
		else return myPow(x*x, n / 2);
	}
	else
	{
		if(n%2==1|| n % 2 == -1)
			return 1/x* myPow(x*x, n / 2);
		else return myPow(x*x, n / 2);
	}
}

• 思路：每次递归时,传递的是x^2以及n/2,
• 举个例子：2^8 = 4^4 = 8^2，每次将n的值折半,就能够大大降低递归深度
• 注意:对n要进行奇偶判断,当n为奇数时,由于折半,以及n为整数int型,因此传递回的将是n的整数部分,而小数部分需要乘入其中才能使值不发生改变------其实就是上一层的x。
• 奇偶判断的例子:

 x=2,n= 5:
 2^5 = 4^2.5 = 4^2*2
 
 x=2,n=-5:
 2^-5=4^-2.5=4^-2*(1/2)

---

53.最大子序列和

---

该题目为求最大子序列和,相对而言比起求和的同时记录起点和终点的题目稍微简化。

• 最初的想法为O(n^2)复杂度的暴力求解,不过这道题目算是一道动态规划的问题,可以使用更加简便的方法求解。
• O（n）复杂度解法：

int maxSubArray(int* nums, int numsSize)
{
  int max=nums[0];
  int nowsum=0;
  for(int i=0;i<numsSize;i++)
  {
      nowsum+=nums[i];
      if(nowsum>max)
        max=nowsum;
      if(nowsum<0)
        nowsum=0;
  }
  return max;
}

• 思路为：设置一个max记录最大子序和，设置nowsum记录当前的子序和,从头遍历一遍数组,可得到结果。
• 如果nowsum大于当前max,则更新max的值
• 由于nowsum在循环中持续加入数组元素,但是加入的数值可能使其变大或者变小,但是我们需要求的是max,因此不关心nowsum是增大或者减小,而是关心其大于0还是小于0。
• 当nowsum小于0时,其实已经没有必要以当前的序列再加下去了

例如：
[1,3,-5,3]
上方序列
当循环进行到第二个元素时,max=4,nowsum=4
而加入-5后nowsum=-1，max=4
此时对于以第0个元素开头的序列其实已经没有必要再加下去了,因为它对之后的元素产生的是负影响
因此直接将nowsum设置为0,此时从相当于从下一个元素进行累计
若其之后的元素之和能够大于max自然就更新，否则max也已经记录了1+3=4这个当前最大的子序列和

• 题目所说的分治算法尚未尝试,可能比起目前的效率还有所提升？

---

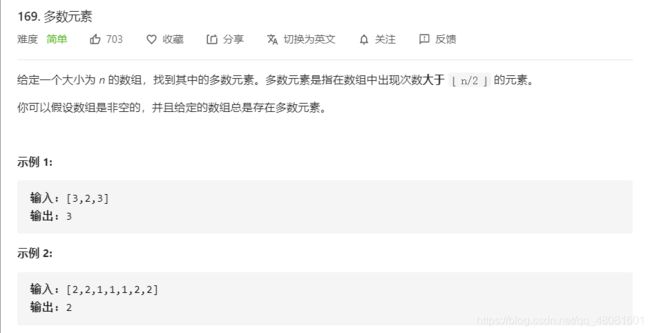
169.多数元素

---

• 最初由于多数元素的性质，即数量大于数组的一半,因此可以知道在数组排序后中间元素必定为所需要的输出（不过最终还是没有尝试排序算法）
• 根据多数元素数量产生的另一种想法,数量大于数组的一半,证明该元素的数量大于其他所有元素之和

int majorityElement(int* nums, int numsSize)
{
    int flag=nums[0];
    int count=0;
    for(int i=0;i<numsSize;i++)
    {
        if(count==0)
        {
            flag=nums[i];
            count++;
        }
        else
        {
            flag==nums[i]?count++:count--;
        }
    }
    return flag;
}

• 设置flag,以及count变量,若当前元素与flag相同,则count+1,否则count-1
• 当count=0时,更新flag的记录元素值
• 对数组进行一次循环后,返回的flag必定为元素数量大于数组长度一半的多数元素

---

• 该方法的名称似乎较摩尔投票法,在评论区中,根据别人的代码,对自己的代码进行了一些微调,时间与空间消耗都有所提升。

---

198.打家劫舍

• 这是一道典型的动态规划问题
• 状态转移方程为dp[i] = max(dp[i - 1], dp[i - 2] + nums[i])

int rob(int* nums, int numsSize)
{
    if(numsSize==0)
        return 0;
    if(numsSize==1)
        return nums[0];
    int a=nums[0];
    int b=nums[0]>=nums[1]?nums[0]:nums[1];
    for(int i=2;i<numsSize;i++)
    {
        int temp=b;
        b=(a+nums[i])>b?(a+nums[i]):b;
        a=temp;
    }
    return b;
}

• 其中a记录的是上一次的状态,b记录当前状态

---

5.最长回文子串

• 当看到题目的时候,心里有个O(N^2)的想法,但是总感觉可能效率较低,始终没有去coding,后来实在想不出效率更高的方法,不得已看了评论区的开源,发现动态规划法的效率也是O(N ^2)级别,于是动手实现了一下自己之前的想法(似乎在评论区的开源中也是一种方法,称为中心扩展法)
• 而且确实有着O(N)级别的算法,马拉车算法(尚未尝试)

char * longestPalindrome(char * s)
{
	int len = strlen(s);
	if (!len)
		return "";
	int maxlen = 1;
	int low = 0;
	int high = 0;
	for (int i = 0; s[i] != 0; i++)
	{
		if (s[i] == s[i + 1])//偶数情况判断
		{
			int nowlow, nowhigh;
			int nowmax;
			for (int n = 0; n <=len / 2; n++)
			{
				if (i - n >= 0 && i + 1 + n < len)
				{
					if (s[i - n] == s[i + 1 + n])
					{
						nowlow = i - n;
						nowhigh = i + n + 1;
						nowmax = nowhigh - nowlow+1;
					}
					else
						break;
					if (nowmax > maxlen)
					{
						low = nowlow;
						high = nowhigh;
						maxlen = nowmax;
					}
				}
				else break;
			}
		}
		if ((i >= 1) && (s[i - 1] == s[i + 1]))//奇数情况判断
		{
			int nowlow, nowhigh;
			int nowmax;
			for (int n = 1; n <=len / 2; n++)
			{
				if (i - n >= 0 && i + n < len)
				{
					if (s[i - n] == s[i + n])
					{
						nowlow = i - n;
						nowhigh = i + n ;
						nowmax = nowhigh - nowlow+1;
					}
					else
						break;
					if (nowmax > maxlen)
					{
						low = nowlow;
						high = nowhigh;
						maxlen = nowmax;
					}
				}
				else break;
			}
		}
	}
	s[high + 1] = '\0';
	s = s + low;
	return s;
}

• 该题代码量比起其他题目明显增加了许多,主要是在将大体思路实现后,总是在某些测试用例上出现些许问题,然后修修改改,修改bug的时间比将框架写起来的时间还要长。
• 最后的两行代码主要用于将子串截取。
• 思路：

1、将回文子串分为两种类别:子串长度为奇数、子串长度为偶数
2、奇数:从子串中心向两边扩展,加上或减去同样的值时,元素应当相等
3、偶数:由于数量原因,无法直接得到子串中心的下标元素,只能通过判断子串中心为两个相同的元素,
从而向两边扩展。

---

674.最长连续递增序列

• 这道题目感觉没什么好说的,相当简单的题目

int findLengthOfLCIS(int* nums, int numsSize)
{
    if(numsSize<2)
        return numsSize;
    int max=0;
    int nowmax=1;
    for(int i=0;i<numsSize-1;i++)
    {
        if(nums[i+1]>nums[i])
            nowmax+=1;
        else nowmax=1;
        if(nowmax>max)
            max=nowmax;
    }
    return max;
}

• 使用nowmax记录当前连续的子序列长度,当其大于max时,更换max,而当数组中发生了一次未递增时,将nowmax重新初始化。
  

---