2018 东北赛 Spin A Web （曼哈顿距离最小生成树）

7231: Spin A Web

时间限制: 1 Sec  内存限制: 128 MB
提交: 100  解决: 12
[提交] [状态] [讨论版] [命题人:admin]

题目描述

We have a canvas divided into grid with H rows and W columns. The square at the ith row from the top and the jth  column from the left is represented as (i, j). (i, j) square has two value xi,j  and yi,j .
Now we want to merge the squares to a connected web with minimal cost. Two squares can be connected if they are in the same row or column, and the cost of connecting (i0, j0) and (i1, j1) is
|xi0,j0 − xi1,j1 | + |yi0,j0 − yi1,j1 |.

 

输入

Input is given from Standard Input in the following format:
H W
x1,1 x1,2  . . . x1,W
.
.
xH,1 xH,2  . . . xH,W
y1,1 y1,2  . . . y1,W
.
.
yH,1 yH,2  . . . yH,W
Constraints
1 ≤ H × W ≤ 100000
−108 ≤ xi,j, yi,j ≤ 108(1 ≤ i ≤ H, 1 ≤ j ≤ W )
All of them are integers.

 

输出

Print one line denotes the minimal cost to merge the square to be a connected web.

 

样例输入

1 3
1 3 2
1 2 3

 

样例输出

5

 

来源/分类

2018东北四省赛 

 

这道题的AC之路特别艰辛，我到最后都不知道我原来的程序为什么跑步过去。。。。

这是一个曼哈顿距离最小生成树的题，我们当时参加了省赛，最后一个简单的题没有水出来，与银牌擦肩而过

拿了三等奖。。。

这是与省赛第二天的东北赛的题目,如今又重现了。看到当时的榜单貌似只有一个人做了出来，然而这道题我也不太清楚坑点

在哪里。

曼哈顿最小距离生成树的学习博客：

https://www.cnblogs.com/xzxl/p/7237246.html

 

说一下我的理解：

对于平面上的n个点我们要求最小生成树是要预处理两两之间的曼哈顿距离，时间花费是n*n的，但是由于两点之间的花费是

曼哈顿距离，我们就有了优化的方法，这里其实是由很多无用边存在的。我们筛掉无用边之后最多只有4*n条边这个时候我们

求最小生成树的时间复杂度就变成了n*logn。

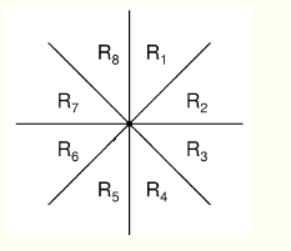
例如 假设当前点的位置在原点，在y轴向右旋转45度的范围内的点，只会有一个点与位于原点这个点相连。

具体的证明在上边的博客。

设i（x1,y1） j(x2,y2)   设i位于原点则，j在R1范围内的条件是 y2-x2>y1-x1(斜率大于1)，并且x2>x1，

两点之间的曼哈顿距离为 |y2-y1|+|x2-x1|  = y2+x2-(y1+x1)  由于y1+x1为定值，对于i点我们只需要求在

R1范围内 x>x1 并且 y-x> y1-x1 并且x+y最小的点。

如何实现：

1.对于x>x1 我们只需要按照x的值排序就能解决

2.如何保证 x+y最小， 对于每一个要查询的点 我们都查询位于他的横坐标之后的（y-x>要查询的）x+y最小的点

这一个可以用树状数组解决（树状数组维护一个（1-n）或者（i-n）的最大值，本题是维护了i到n的最大值）。

3.如何保证查询到的点的y-x>当前的y1-x1， 我们按照y-x的值排序，对于每一个a[i]的值（见下方代码）

pos之后的y-x肯定要比当前的y-x大，（位置可用二分来确定），又因为我们是倒叙遍历a[i]的，所以先插进去的点

都是在当前点后边的点，然后当前点pos的值我们更新为x+y并且记录id。

4.处理完R1区间还有R2 R3 ....,其实这些区间我们可以用区间变换把左边转移到R1区间，然后用处理R1区间的方法处理这些区间

，由于边是双向边，所以我们只需要处理位于原点（每个查询点都可以看作原点）右边的点。

具体的坐标变换过程如下：

对于第二步和第四步,我们按y=x翻转,即交换横纵坐标，第三部关于y轴对称一下。就将其他三个区间里的点都转换到R1范围内了。

 

对于本题有个限制就是只能合并同一行或者同一列，所以我们对每一行和每一列做一次曼哈顿距离就行。

 

#include
#include
#include
#include
#include
using namespace std;
#define LL long long
#define inf 2000000000
#define N 100015
#define lowb(x) (x&-x)
inline int read()
{
    char c;
    int sum=0;
    int f=1;
    c=getchar();
    while(c<'0'||c>'9')
    {
        if(c=='-')f=-1;
        c=getchar();
    }
    while(c>='0'&&c<='9')
    {
        sum=sum*10+c-'0';
        c=getchar();
    }
    return sum*f;
}
int aa[N],cc[N];
 
void add(int p,int val,int id)
{
    while(p>0)
    {
        if(aa[p]>val)
        {
            aa[p]=val;
            cc[p]=id;
        }
        p-=lowb(p);
    }
}
int query(int p,int n)
{
    int m=inf;
    int ans=-1;
    while(p<=n)
    {
        if(aa[p]=0; i--)
    {
        int pos=lower_bound(b,b+kk,a[i])-b+1;
        int ans=query(pos,n);
        if(ans!=-1)
        {
            edg[tot].u=p1[p[i]].id;
            edg[tot].v=p1[p[ans]].id;
            edg[tot].k=abs(p1[p[i]].x-p1[p[ans]].x)+abs(p1[p[i]].y-p1[p[ans]].y);
            tot++;
        }
        add(pos,p1[p[i]].x+p1[p[i]].y,i);
    }
}
 
void Flip(int n)
{
    for(int i=0; i<4; i++)
    {
        for(int j=0; j

附上原来一直超时的代码

#include
#include
#include
#include
#include
using namespace std;
#define LL long long
#define inf 2000000000
#define N 100015
#define lowb(x) (x&-x)
inline int read()
{
    char c;
    int sum=0;
    int f=1;
    c=getchar();
    while(c<'0'||c>'9')
    {
        if(c=='-')f=-1;
        c=getchar();
    }
    while(c>='0'&&c<='9')
    {
        sum=sum*10+c-'0';
        c=getchar();
    }
    return sum*f;
}
struct BIT
{
    int a[N],c[N];
    void init(){
    for(int i=1;i<=N;i++)a[i]=inf,c[i]=-1;
    }
    void add(int p,int val,int id)
    {
        while(p>0)
        {
            if(a[p]>val)
            {
                a[p]=val;
                c[p]=id;
            }
            p-=lowb(p);
        }
    }
 
    int query(int p,int n)
    {
        int m=inf;
        int ans=-1;
        while(p<=n)
        {
            if(a[p]=0;i--)
    {
        int pos=lower_bound(b,b+kk,a[i])-b+1;
        int ans=T.query(pos,n);
        if(ans!=-1)
        {
            edg[tot].u=p1[p[i]].id;
            edg[tot].v=p1[p[ans]].id;
            edg[tot].k=abs(p1[p[i]].x-p1[p[ans]].x)+abs(p1[p[i]].y-p1[p[ans]].y);
            tot++;
        }
        T.add(pos,p1[p[i]].x+p1[p[i]].y,i);
    }
}
 
void Flip(int n)
{
    for(int i=0;i<4;i++)
    {
        for(int j=0;j

终于知道哪里出错了，我再也不把函数写在一个结构体里装X了。。。。

优化之后200多ms跑过。。

#include
#include
#include
#include
#include
using namespace std;
#define LL long long
#define inf 2000000000
#define N 100015
#define lowb(x) (x&-x)
int aa[N],cc[N];
void add(int p,int val,int id)
{
    while(p>0)
    {
        if(aa[p]>val)
        {
            aa[p]=val;
            cc[p]=id;
        }
        p-=lowb(p);
    }
}
int query(int p,int n)
{
    int m=inf;
    int ans=-1;
    while(p<=n)
    {
        if(aa[p]=1; i--)
    {
        int pos=AA[p[i].id];
        int ans=query(pos,n);
        if(ans!=-1)
        {
            edg[tot].u=p[i].id;
            edg[tot].v=p[ans].id;
            edg[tot].k=abs(p[i].x-p[ans].x)+abs(p[i].y-p[ans].y);
            tot++;
        }
        add(pos,p[i].x+p[i].y,i);
    }
}

void Flip(int n)
{
    for(int i=0; i<4; i++)
    {
        for(int j=1; j<=n; j++)
        {
            if(i==1||i==3)
            {
                swap(p[j].x,p[j].y);
            }
            else if(i==2)
            {
                p[j].x=-p[j].x;
            }
        }
        creat(n);
    }
}

int f[N];
int Find(int x)
{
    return f[x]==x?x:f[x]=Find(f[x]);
}
int w;
int getid(int i,int j)
{

    return i*w+j;
}

int main()
{
    //freopen("ce.txt","r",stdin);
    int h;
    scanf("%d%d",&h,&w);
    int _id=1;
    for(int i=0; i