(树状数组)洛谷 P6119/P3657 Why Did the Cow Cross the Road II G/P 题解
题意
Farmer John 饲养了 N N N 种奶牛,编号从 1 1 1 到 N N N。一些品种的奶牛和其他奶牛间相处良好,事实证明,如果两个品种的奶牛编号分别为 a , b a,b a,b,当 ∣ a − b ∣ ≤ 4 |a-b| \leq 4 ∣a−b∣≤4 时,这两个品种的奶牛能友好相处,否则不能友好相处。
一条长长的道路贯穿整个农场,道路的左侧有 N N N 个牧场(每个品种的奶牛恰好占据一个牧场),道路的右侧也有 N N N 个牧场(每个品种的奶牛恰好占据一个牧场)。为了让奶牛们安全穿过马路,Farmer John 希望能在马路上画出一些人行道(牛行道?),要求这些人行道满足如下条件:
- 人行道从左侧的某个牧场出发,连接到右侧的某个牧场;
- 人行道连接的两个牧场的奶牛要能友好相处;
- 人行道不能在道路中间相交;
- 每个牧场只能与一条人行道相连。
你需要帮 FJ 求出最多能有多少条人行道。
洛谷 P6119: 1 ≤ n ≤ 1000 1\le n\le 1000 1≤n≤1000:;
洛谷 P3657: 1 ≤ n ≤ 1 0 5 1\le n\le 10^5 1≤n≤105。
本题解两个数据范围有不同解法。
思路(小数据)
这个数据支持 Θ ( n 2 ) \Theta(n^2) Θ(n2)。
我们考虑枚举两侧的道路进行匹配。而题目要求道路不能交叉,那么得“一起推进”——其实是 dp。
设 f i , j f_{i,j} fi,j 表示, a a a 数组前 i i i 个、 b b b 数组前 j j j 个的最大匹配数。
如果 ∣ a i − b j ∣ ≤ 4 |a_i-b_j|\le 4 ∣ai−bj∣≤4,那么就可以在左侧的 i i i 和 右侧的 j j j 建立道路(在接下来就不会在出现,左侧小于 i i i 的连接右侧大于 j j j 的的道路了)。
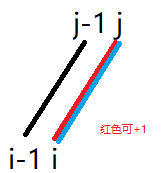
f i , j = max { f i − 1 , j − 1 + 1 } , ∣ a i − b j ∣ ≤ 4 f_{i,j}=\max\{f_{i-1,j-1}+1\},|a_i-b_j|\le 4 fi,j=max{fi−1,j−1+1},∣ai−bj∣≤4
否则就不能建,那么从哪里转移过来呢?跳过 i i i 和 j j j 其中一个点不建边就好了。
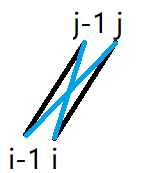
f i , j = max { f i − 1 , j , f i , j − 1 } f_{i,j}=\max\{f_{i-1,j},f_{i,j-1}\} fi,j=max{fi−1,j,fi,j−1}
代码 1
#include思路(大数据)
虽然很典型,但是还是思维有点混乱,这种节点贡献的题目还是要多练。
能否考虑优化小数据的做法呢?省去一个维度?
对每一个 a i a_i ai,枚举可以和它配对的种类区间 [ a i − 4 , a i + 4 ] [a_i-4,a_i+4] [ai−4,ai+4]。
省去一维,设 f i f_i fi 表示,当前,右侧的种类 i i i 对应点 p o s i pos_i posi 作为配对的结尾的最大匹配数,然后更新 p o s i pos_i posi 的贡献为 f i + 1 f_i+1 fi+1。
考虑用树状数组维护。
代码 2
#include