Matlab中的magic函数、vander函数、hilb函数、compan函数、pascal函数、zeros函数、ones函数、eye函数、rand函数、randn函数

通用的特殊矩阵

zeros函数：产生全0矩阵，即零矩阵。
ones函数：产生全1矩阵，即幺矩阵。
eye函数：产生对角线为1的矩阵。当矩阵是方阵时，得到一个单位矩阵。
rand函数：产生（0,1）区间均匀分布的随机矩阵。
randn函数：产生均值为0，方差为1的标准正态分布随机矩阵。

zeros函数的调用格式：
zeros(m)：产生m×m的零矩阵。
zeros(m,n)：产生m×n的零矩阵。
zeros(size(A))；产生与矩阵A同样大小的零矩阵。
其它函数的调用格式同上！！！

>> A=zeros(2,3)
A =
     0     0     0
     0     0     0
>> ones(size(reshape(A,3,2)))
ans =
     1     1
     1     1
     1     1
>> 

例1 首先产生5阶两位随机整数矩阵A，再产生均值为0.6、方差为0.1的5阶正态分布随机矩阵B，最后验证(A+B)*| = |*A + |*B（| 为单位矩阵）。

rand函数：产生（0,1）开区间均匀分布的随机数x。
fix(a+(b-a+1)*x)：产生（a,b）区间上均匀分布的随机整数。
randn函数：产生均值为0、方差为1的标准正态分布随机数x。
μ+σx：得到均值为μ、方差为σ²的随机数。

>> A=fix(10+(99-10+1)*rand(5));
>> B=0.6+sqrt(0.1)*randn(5)
B =
    0.9272    0.8809    1.0549    0.5677    0.5905
    0.8299    0.2373    0.7028    0.5236    0.5479
    0.5040    0.2620    0.3613    0.7009    0.7985
    0.6929    0.3440    1.0333    0.6989    0.9457
    0.3510   -0.3311    0.0588    0.3265    0.9508
>> C=eye(5);
>> (A+B)*C==C*A+C*B
ans =
  5×5 logical 数组

   1   1   1   1   1
   1   1   1   1   1
   1   1   1   1   1
   1   1   1   1   1
   1   1   1   1   1

用于专门学科的特殊矩阵

magic函数、vander函数、hilb函数、compan函数、pascal函数。

1. 魔方矩阵(方阵、magic函数)

>> M=magic(3)
M =
     8     1     6
     3     5     7
     4     9     2

n阶魔方阵由1,2,3…,n共n²个整数组成，且每行、每列以及主、副对角线上各n个元素之和都相等。
n阶魔方阵每行每列元素的和为(1+2+3+…+n²) / n= (n+n³)/2。
Matlab中 magic(n) 只产生一个特定的魔方阵,实际上当n大于2时可能有多个魔方阵存在。

>> M=magic(3);
>> x=sum(M(1,:))
x =
    15
>> y=sum(M(:,1))
y =
    15

2. 范德蒙矩阵(方阵、vander函数)

在Matlab中，函数 vander(V) 生成以向量V为基础的范德蒙矩阵。

>> A=vander(1:5)
A =
     1     1     1     1     1
    16     8     4     2     1
    81    27     9     3     1
   256    64    16     4     1
   625   125    25     5     1

3. 希尔伯特矩阵(方阵、hilb函数)

>> H=hilb(4)
H =
    1.0000    0.5000    0.3333    0.2500
    0.5000    0.3333    0.2500    0.2000
    0.3333    0.2500    0.2000    0.1667
    0.2500    0.2000    0.1667    0.1429

format函数：控制输出格式。
format rat ：使用分数来表示数值

>> format rat
>> H=hilb(4)
H =
       1              1/2            1/3            1/4     
       1/2            1/3            1/4            1/5     
       1/3            1/4            1/5            1/6     
       1/4            1/5            1/6            1/7     

4. 伴随矩阵(方阵、compan函数)

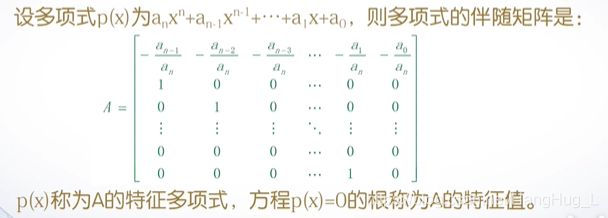
Matlab生成伴随矩阵的函数是 compan()，其中p是一个多项式的系数向量，高次幂系数排在前，低次幂系数排在后。

>> p=[1,-2,-5,6];   //对应 a3 a2 a1 a0，是一个3阶方阵
>> A=compan(p)
A =
     2     5    -6
     1     0     0
     0     1     0

5. 帕斯卡矩阵(方阵、pascal函数)

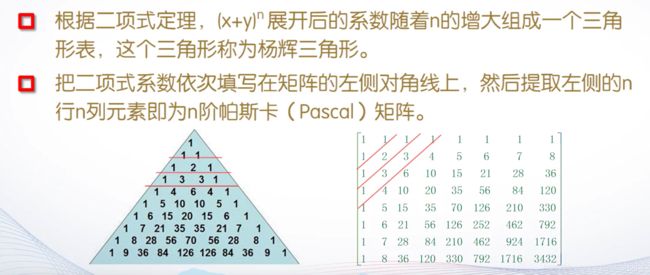
>> P=pascal(5)
P =
     1     1     1     1     1
     1     2     3     4     5
     1     3     6    10    15
     1     4    10    20    35
     1     5    15    35    70
>> inv(P)     //求矩阵P的逆矩阵
ans =
    5.0000  -10.0000   10.0000   -5.0000    1.0000
  -10.0000   30.0000  -35.0000   19.0000   -4.0000
   10.0000  -35.0000   46.0000  -27.0000    6.0000
   -5.0000   19.0000  -27.0000   17.0000   -4.0000
    1.0000   -4.0000    6.0000   -4.0000    1.0000