Python小白 Leetcode刷题历程 No.66-No.70 加一、二进制求和、文本左右对齐、x的平方根、爬楼梯 （有题干 有代码 有思路心得）

Python小白 Leetcode刷题历程 No.66-No.70 加一、二进制求和、文本左右对齐、x的平方根、爬楼梯

写在前面：

作为一个计算机院的大学生，总觉得仅仅在学校粗略的学习计算机专业课是不够的，尤其是假期大量的空档期，作为一个小白，实习也莫得路子，又不想白白耗费时间。于是选择了Leetcode这个平台来刷题库。编程我只学过基础的C语言，现在在自学Python，所以用Python3.8刷题库。现在我Python掌握的还不是很熟练，算法什么的也还没学，就先不考虑算法上的优化了，单纯以解题为目的，复杂程度什么的以后有时间再优化。计划顺序五个题写一篇日志，希望其他初学编程的人起到一些帮助，写算是对自己学习历程的一个见证了吧。

有一起刷LeetCode的可以关注我一下，我会一直发LeetCode题库Python3解法的，也可以一起探讨。

觉得有用的话可以点赞关注下哦，谢谢大家！
········································································································································································

No.66.加一

难度：简单
题目描述：

题解代码（Python3.8）

class Solution:
    def plusOne(self, digits: List[int]) -> List[int]:
        digits=[str(x) for x in digits]
        digits="".join(digits)
        digits=int(digits)
        digits+=1
        digits=str(digits)
        digits=[int(x) for x in digits]
        return digits
        #这道题写成一句话就（return [int(x) for x in str(int(''.join([str(i) for i in digits])) + 1)] ）

解题思路：
先将数组转换成字符串，再将字符串转换成整数，再将整数加一，之后将整数转换成字符串，最后将字符串转换成数组。

优解代码及分析：
优解代码（Python3.8）

class Solution:
    def plusOne(self, digits: List[int]) -> List[int]:
        return [int(x) for x in str(int(''.join([str(i) for i in digits])) + 1)] 

分析：
就是将题解代码写成了一句话形式，本质没有变，降低了可读性，减少了代码量。

No.67.二进制求和

难度：简单
题目描述：

题解代码（Python3.8）

class Solution:
    def addBinary(self, a: str, b: str) -> str:
        l_a,l_b=len(a),len(b)
        if l_a < l_b:
            a,b=b,a
            l_a,l_b=l_b,l_a
        a,b=a[::-1],b[::-1]
        
        if l_a > l_b:
            count=l_a-l_b
            while count>0:
                b += '0'
                count-=1
        
        a=[ x for x in a]
        carry=0
        for i in range(l_a):
            add=int(a[i])+int(b[i])+carry
            carry=add//2
            if add < 2:
                a[i]=str(add)
            else:
                add -=2
                a[i]=str(add)
        if carry==1:
            a.append('1')
                             
        a="".join(a)
        return a[::-1]

解题思路：
这道题的思路就是竖式加法。
判断a和b那个更长，另较长的为a，将a，b反向切片，b尾端补0至与a等长。令a为列表形式，a和b逐位相加，注意进位，最后将a以字符串的形式反向输出即可。

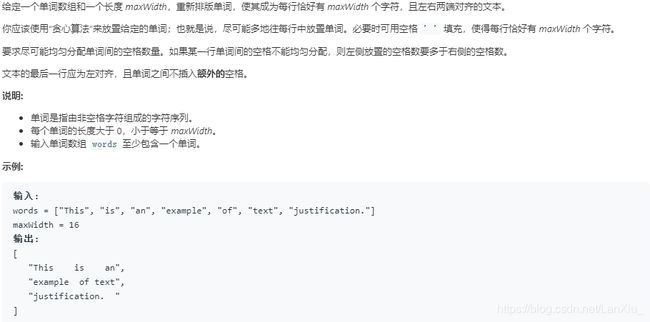
No.68.文本左右对齐

难度：困难
题目描述：

题解代码（Python3.8）

class Solution:
    def fullJustify(self, words: List[str], maxWidth: int) -> List[str]:
        res = []   # 最后的答案
        cur_chars = 0  # 当前行的字母数
        cur_words = 0  # 当前行的单词数
        words_list = []    # 当前行的单词列表
        for i, word in enumerate(words):
            l = len(word)
            if cur_chars + l + cur_words > maxWidth: # 加上这个单词是否会超过最大长度
                if cur_words == 1: # 当前行仅有一个超长的单词，后面全部补空格
                    res.append(words_list[0] + ' ' * (maxWidth-cur_chars))
                else:
                    left = maxWidth - cur_chars # 这行一共有几个空格
                    if left % (cur_words-1) == 0: # 空格刚好平均分配
                        res.append((' '*(left//(cur_words-1))).join(words_list))
                    else: # 空格不能平均分配
                        x = left % (cur_words-1)  # 多余的空格
                        b = left // (cur_words-1) # 平均每个间隔最少的空格数
                        cans = words_list[0]
                        for i in range(x): # 前 x 个间隔空 b + 1 个
                            cans += ' ' * (b+1) + words_list[i+1]
                        for i in range(x+1, len(words_list)): # 后面的都空 b 个
                            cans += ' ' * b + words_list[i]
                        res.append(cans)
                cur_chars = l
                cur_words = 1
                words_list = [word]
            else:
                cur_chars += l
                cur_words += 1
                words_list.append(word)

        if cur_words > 0: # 所有单词过完了把余下的词放入最后一行
            cans = ' '.join(words_list)
            cans += ' ' * (maxWidth - len(cans))
            res.append(cans)
        return res

或许有用的知识点：
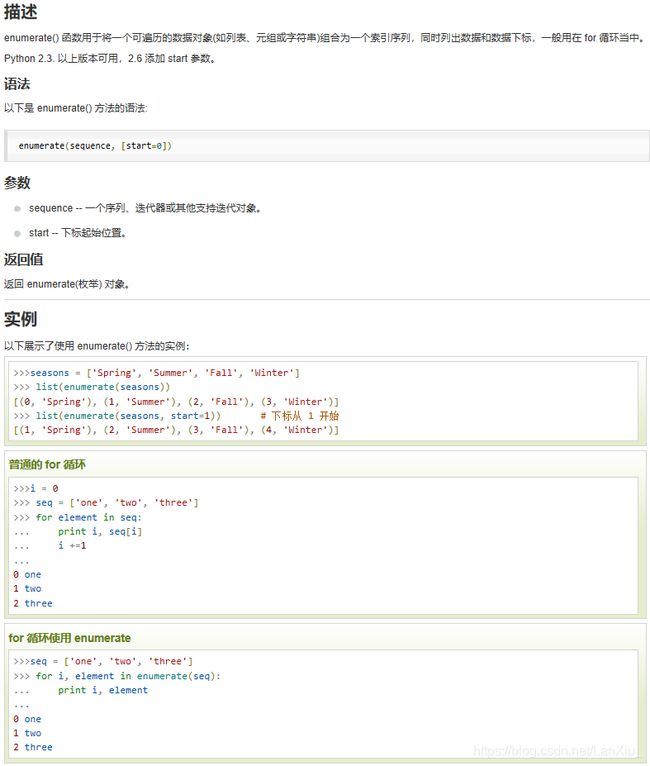
这道题可以用到python的enumerat()函数，enumerate()函数的部分介绍如下

解题思路：
一共有以下变量：res最后的结果、cur_chars当前行的字母数、cur_words当前行的单词数、
word_list当前行的单词列表。
然后一个单词一个单词的过，判断加上这个单词是否会超过最大长度，一行的最低长度是：
cur_chars + cur_words - 1，如果这个大于maxWidth，就把这一行加入res中。所有单词过完了再把余下的词放入最后一行。再看如何安排每一行的单词：如果这一行只有一个单词，单词左对齐，后面补满空格；一行多个单词，空格正好可以平均分配，求出平均每个间隔几个空格，直接用 python 字符串的 join 方法就可以了；有多余的空格，题目要求左边空格多于右边，先算算平均每个间隔几个空格，然后余下几个，如果平均 b 个，余下 x 个，则前 x 个间隔空 b + 1 个，后面的都空 b 个。

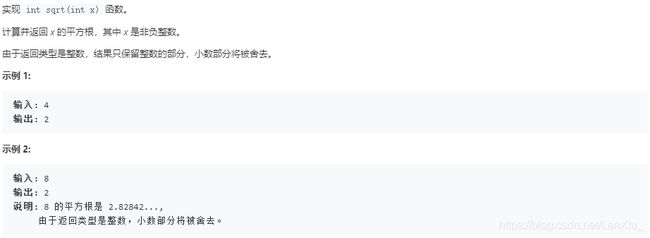
No.69.x的平方根

难度：简单
题目描述：

题解代码（Python3.8）

class Solution:
    def mySqrt(self, x: int) -> int:
        if x ==0:
            return 0
        left=1
        right=x//2
        while left<right:
            mid = (left+right+1)//2  #这里一定要取右中位数，画图理解即可
            square = mid*mid
            if square>x:
                right = mid-1
            else:
                left = mid
        return left

或许有用的知识点：
这道题要用到二分查找的方法。

解题思路：
用二分法搜索平方根的思想很简单，就类似于小时候我们看的电视节目中的“猜价格”游戏，高了就往低了猜，低了就往高了猜，范围越来越小。因此，使用二分法猜算术平方根就很自然。一个数的平方根肯定不会超过它自己，不过直觉还告诉我们，一个数的平方根最多不会超过它的一半，我们发现如果一个非负数的一半的平方大于它自己，那么这个数>=4.我们考虑一下0，1，2，3的平方根为0，1，1，1（不考虑特值可能会出错）。之后套用二分查找的模板即可，注意这道题中位数我们要选择右中位数（找个例子画个图就很容易理解了）。

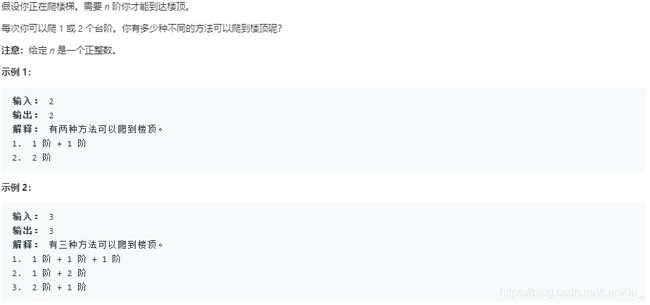
No.70.爬楼梯

难度：简单
题目描述：

题解代码（Python3.8）

class Solution:
    def climbStairs(self, n: int) -> int:
        if n<=2:
            return 1 if n==1 else 2
        dp=[ 0 for x in range(n)]
        dp[0],dp[1]=1,2

        for i in range(2,n):
            dp[i]=dp[i-1]+dp[i-2]

        return dp[n-1]

或许有用的知识点：
这道题要用到动态规划的方法，是经典的动态规划算法题目之一。

解题思路：
这道题是经典的动态规划算法题，我们可以套用动态规划算法的模板，对于这道题，令dp[n]为爬上n阶台阶的方法总数，假定n=10,首先考虑最后一步的情况,要么从第九级台阶再走一级到第十级,要么从第八级台阶走两级到第十级,因而,要想到达第十级台阶,最后一步一定是从第八级或者第九级台阶开始.也就是说已知从地面到第八级台阶一共有X种走法,从地面到第九级台阶一共有Y种走法,那么从地面到第十级台阶一共有X+Y种走法。即F(10)=F(9)+F(8)分析到这里,动态规划的三要素出来了：
状态：例如，F(10)的最优子结构即F(9)和F(8)，依此类推 。
状态转移方程：F(n)=F(n-1)+F(n-2)
边界条件：F(1)=1,F(2)=2