概率论中多元随机变量函数分布中的卷积公式原来是重积分换元
文章目录
- 重积分换元(雅克比行列式)
- 卷积公式
- ①:把$x$换掉
- 确定范围
- 卷积公式做
- 定义法来做
- Z=max{X,Y}
- Z=min{X,Y}
重积分换元(雅克比行列式)
{ x = x ( u , v ) y = y ( u , v ) \left\{\begin{matrix} x=x(u,v)\\ \\ y=y(u,v) \end{matrix}\right. ⎩⎨⎧x=x(u,v)y=y(u,v)
J = ∣ ∂ x ∂ u ∂ x ∂ v ∂ y ∂ u ∂ y ∂ v ∣ J=\begin{vmatrix} \frac{\partial x}{\partial u}&\frac{\partial x}{\partial v}\\ \\\frac{\partial y}{\partial u} &\frac{\partial y}{\partial v} \end{vmatrix} J=∣∣∣∣∣∣∂u∂x∂u∂y∂v∂x∂v∂y∣∣∣∣∣∣
d x d y = d [ x ( u , v ) ] d [ y ( u , v ) ] = ∣ J ∣ ⋅ d u d v dxdy=d[x(u,v)]d[y(u,v)]=|J|\cdot dudv dxdy=d[x(u,v)]d[y(u,v)]=∣J∣⋅dudv
卷积公式
①: Z = X + Y Z=X+Y Z=X+Y
f z ( z ) = ∫ − ∞ + ∞ f ( z − y , y ) d y = ∫ − ∞ + ∞ f ( x , z − x ) d x f_{z}(z)=\int_{-\infty}^{+\infty} f(z-y, y) \mathrm{d} y=\int_{-\infty}^{+\infty} f(x, z-x) \mathrm{d} x fz(z)=∫−∞+∞f(z−y,y)dy=∫−∞+∞f(x,z−x)dx
②: Z = X ⋅ Y Z=X\cdot Y Z=X⋅Y
f Z ( z ) = ∫ − ∞ + ∞ 1 ∣ x ∣ f ( x , z x ) d x = ∫ − ∞ + ∞ 1 ∣ y ∣ f ( z y , y ) d y f_{Z}(z)=\int_{-\infty}^{+\infty} \frac{1}{|x|} f\left(x, \frac{z}{x}\right) \mathrm{d} x=\int_{-\infty}^{+\infty} \frac{1}{|y|} f\left(\frac{z}{y}, y\right) \mathrm{d} y fZ(z)=∫−∞+∞∣x∣1f(x,xz)dx=∫−∞+∞∣y∣1f(yz,y)dy
③: Z = X Y Z=\frac{X}{Y} Z=YX
f Z ( z ) = ∫ − ∞ + ∞ ∣ y ∣ f ( y z , y ) d y f_{Z}(z)=\int_{-\infty}^{+\infty}|y| f(y z, y) \mathrm{d} y fZ(z)=∫−∞+∞∣y∣f(yz,y)dy
以前学的时候,第一个公式感觉还能理解:就跟求边缘概率密度一个意思,积分掉一个变量就只剩另外一个了,那现在有三个变量也不来头,因为三个变量之间有关系,第三个变量阔以用另外两个变量表示出来,然后再积分掉一个,就只剩下一个了
but,yet,however,nevertheless,为啥后两个公式里面还多了一坨东西喃?
直到在b站上一不小心看到这位阿婆主的视频才知道
这里是 等待崛起 这位童鞋的视频b站链接谢谢分享(๑◡๑)
在此让朕来总结一哈
①:把 x x x换掉
F ( x , y ) = ∬ f ( x , y ) d x d y , 把 x 用 x = x ( y , z ) 换 掉 F [ x ( y , z ) , y ] = ∬ f [ x ( y , z ) , y ] d [ x ( y , z ) ] d y F(x,y)=\iint f(x,y)dxdy,\\把x用x=x(y,z)换掉\\F[x(y,z),y]=\iint f[x(y,z),y]d[x(y,z)]dy F(x,y)=∬f(x,y)dxdy,把x用x=x(y,z)换掉F[x(y,z),y]=∬f[x(y,z),y]d[x(y,z)]dy
然后利用雅克比行列式把换元后的微元换掉
{ x = x ( y , z ) y = y \left\{\begin{matrix} x=x(y,z)\\ \\y=y \end{matrix}\right. ⎩⎨⎧x=x(y,z)y=y
J = ∣ ∂ x ∂ y ∂ x ∂ z ∂ y ∂ y ∂ y ∂ z ∣ = J = ∣ ∂ x ∂ y ∂ x ∂ z 1 0 ∣ = − ∂ x ∂ z , 正 负 没 关 系 , 反 正 后 面 要 加 绝 对 值 J=\begin{vmatrix} \frac{\partial x}{\partial y}&\frac{\partial x}{\partial z} \\ \frac{\partial y}{\partial y}&\frac{\partial y}{\partial z} \end{vmatrix}=J=\begin{vmatrix} \frac{\partial x}{\partial y}&\frac{\partial x}{\partial z} \\ 1&0 \end{vmatrix}=-\frac{\partial x}{\partial z},正负没关系,反正后面要加绝对值 J=∣∣∣∣∣∂y∂x∂y∂y∂z∂x∂z∂y∣∣∣∣∣=J=∣∣∣∣∂y∂x1∂z∂x0∣∣∣∣=−∂z∂x,正负没关系,反正后面要加绝对值
因此 d x d y = ∣ J ∣ d y d z = ∣ − ∂ x ∂ z ∣ d y d z dxdy=|J|dydz=|-\frac{\partial x}{\partial z}|dydz dxdy=∣J∣dydz=∣−∂z∂x∣dydz
因此 ∬ f [ x ( y , z ) , y ] d [ x ( y , z ) ] d y = ∬ f [ x ( y , z ) , y ] ∣ J ∣ d y d z = ∫ [ ∫ f [ x ( y , z ) , y ] ∣ J ∣ d y ] d z = ∫ f Z ( z ) d z , 这 里 外 层 中 括 号 括 起 来 的 就 是 z 的 边 缘 概 率 密 度 f Z ( z ) \iint f[x(y,z),y]d[x(y,z)]dy=\iint f[x(y,z),y]|J|dydz=\int[\int f[x(y,z),y]|J|dy]\ dz=\int f_Z(z)dz,这里外层中括号括起来的就是z的边缘概率密度f_Z(z) ∬f[x(y,z),y]d[x(y,z)]dy=∬f[x(y,z),y]∣J∣dydz=∫[∫f[x(y,z),y]∣J∣dy] dz=∫fZ(z)dz,这里外层中括号括起来的就是z的边缘概率密度fZ(z)
这 样 就 得 到 了 f Z ( z ) = ∫ f [ x ( y , z ) , y ] ∣ J ∣ d y 这样就得到了f_Z(z)=\int f[x(y,z),y]|J|dy 这样就得到了fZ(z)=∫f[x(y,z),y]∣J∣dy
我们这里的 ∣ J ∣ = ∣ − ∂ x ∂ z ∣ |J|=|-\frac{\partial x}{\partial z}| ∣J∣=∣−∂z∂x∣,来验证一哈喃
当 Z = X + Y Z=X+Y Z=X+Y时: ∣ − ∂ x ∂ z ∣ = 1 |-\frac{\partial x}{\partial z}|=1 ∣−∂z∂x∣=1
当 Z = X ⋅ Y Z=X\cdot Y Z=X⋅Y时: ∣ − ∂ x ∂ z ∣ = ∣ 1 y ∣ |-\frac{\partial x}{\partial z}|=|\frac{1}{y}| ∣−∂z∂x∣=∣y1∣
当 Z = X Y Z=\frac{X}{Y} Z=YX时: ∣ − ∂ x ∂ z ∣ = ∣ y ∣ |-\frac{\partial x}{\partial z}|=|y| ∣−∂z∂x∣=∣y∣
对滴~(✪ω✪)
确定范围
卷积公式做
这种题就是知道上面还不行,考的就是考确定范围,就以2005年数学一的第22题作为例子吧
题 意 : f ( x , y ) = { 1 , 0 < x < 1 , 0 < y < 2 x 0 , 其 他 , 求 Z = 2 Z − Y 的 概 率 密 度 f Z ( z ) 题意:f(x,y)=\left\{\begin{matrix} 1,0
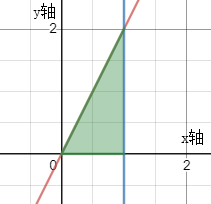
将 x = y + z 2 代 入 范 围 { 0 < x < 1 ⇒ 0 < y + z 2 < 1 ⇒ { y > − z y < − z + 2 0 < y < 2 x ⇒ 0 < y < y + z ⇒ { y > 0 z > 0 ⇒ { y > − z y < − z + 2 y > 0 z > 0 x=\frac{y+z}{2}代入范围\left\{\begin{matrix} 0
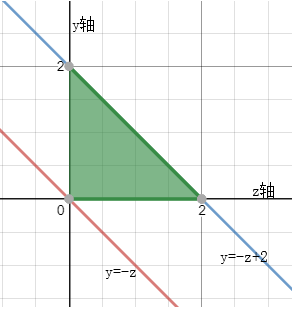
然后就相当于求z的边缘概率密度了
很明显,只有在 0 < z < 2 0
我们把 y y y积分掉: f Z ( z ) = ∫ 0 − z + 2 f [ x ( y , z ) , y ] ⋅ ∣ J ∣ d y = ∫ 0 − z + 2 1 ⋅ 1 2 d y = 1 − z 2 f_Z(z)=\int_0^{-z+2}f[x(y,z),y]\cdot|J|dy=\int_0^{-z+2}1\cdot \frac{1}{2}dy=1-\frac{z}{2} fZ(z)=∫0−z+2f[x(y,z),y]⋅∣J∣dy=∫0−z+21⋅21dy=1−2z
定义法来做
F Z ( z ) = P { Z ≤ z } = P { 2 X − Y ≤ z } F_Z(z)=P\{Z\leq z\}=P\{2X-Y\leq z\} FZ(z)=P{Z≤z}=P{2X−Y≤z}
也就是 y ≥ 2 x − z y\geq 2x-z y≥2x−z这个区域怎么才能与第一张图上的阴影部分有交集,观察y轴截距,只有当 − 2 < − z < 0 -2<-z<0 −2<−z<0的时候才行
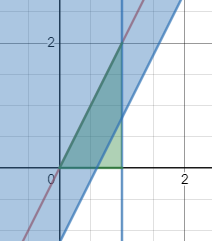
也就是算这个梯形的面积,阔以用1来减去小三角形的面积
完了还要对z求导
顺便记一哈这两个特殊的
Z=max{X,Y}
F Z ( z ) = P { Z ≤ z } = P { m a x { X , Y } ≤ z } = P { X ≤ z , Y ≤ z } = P { X ≤ z } ⋅ { Y ≤ z } = F X ( z ) ⋅ F Y ( z ) F_Z(z)=P\{Z\leq z\}=P\{max\{X,Y\}\leq z\}=P\{X\leq z,Y\leq z\}=P\{X\leq z\}\cdot\{Y\leq z\}=F_X(z)\cdot F_Y(z) FZ(z)=P{Z≤z}=P{max{X,Y}≤z}=P{X≤z,Y≤z}=P{X≤z}⋅{Y≤z}=FX(z)⋅FY(z)
Z=min{X,Y}
F Z ( z ) = P { Z ≤ z } = P { m i n { X , Y } ≤ z } = 1 − P { m i n { X , Y } > z } = 1 − P { X > z } ⋅ P { Y > z } = 1 − [ 1 − P { X ≤ z } ] ⋅ [ 1 − P { Y ≤ z } ] = 1 − [ 1 − F X ( z ) ] ⋅ [ 1 − F Y ( z ) ] F_Z(z)=P\{Z\leq z\}=P\{min\{X,Y\}\leq z\}=1-P\{min\{X,Y\}> z\}=1-P\{X> z\}\cdot P\{Y>z\}\\ =1-[1-P\{X\leq z\}]\cdot [1-P\{Y\leq z\}]=1-[1-F_X(z)]\cdot [1-F_Y(z)] FZ(z)=P{Z≤z}=P{min{X,Y}≤z}=1−P{min{X,Y}>z}=1−P{X>z}⋅P{Y>z}=1−[1−P{X≤z}]⋅[1−P{Y≤z}]=1−[1−FX(z)]⋅[1−FY(z)]