并查集训练题解(F-J)

训练链接：http://acm.njupt.edu.cn/vjudge/contest/view.action?cid=173#overview

F题 Navigation Nightmare

Time Limit: 2000MS		Memory Limit: 30000K
Total Submissions: 4599		Accepted: 1734
Case Time Limit: 1000MS

Description

Farmer John's pastoral neighborhood has N farms (2 <= N <= 40,000), usually numbered/labeled 1..N. A series of M (1 <= M < 40,000) vertical and horizontal roads each of varying lengths (1 <= length <= 1000) connect the farms. A map of these farms might look something like the illustration below in which farms are labeled F1..F7 for clarity and lengths between connected farms are shown as (n):

           F1 --- (13) ---- F6 --- (9) ----- F3

            |                                 |

           (3)                                |

            |                                (7)

           F4 --- (20) -------- F2            |

            |                                 |

           (2)                               F5

            | 

           F7 

Being an ASCII diagram, it is not precisely to scale, of course.

Each farm can connect directly to at most four other farms via roads that lead exactly north, south, east, and/or west. Moreover, farms are only located at the endpoints of roads, and some farm can be found at every endpoint of every road. No two roads cross, and precisely one path
(sequence of roads) links every pair of farms.

FJ lost his paper copy of the farm map and he wants to reconstruct it from backup information on his computer. This data contains lines like the following, one for every road:

There is a road of length 10 running north from Farm #23 to Farm #17
There is a road of length 7 running east from Farm #1 to Farm #17
...

As FJ is retrieving this data, he is occasionally interrupted by questions such as the following that he receives from his navigationally-challenged neighbor, farmer Bob:

What is the Manhattan distance between farms #1 and #23?

FJ answers Bob, when he can (sometimes he doesn't yet have enough data yet). In the example above, the answer would be 17, since Bob wants to know the "Manhattan" distance between the pair of farms.
The Manhattan distance between two points (x1,y1) and (x2,y2) is just |x1-x2| + |y1-y2| (which is the distance a taxicab in a large city must travel over city streets in a perfect grid to connect two x,y points).

When Bob asks about a particular pair of farms, FJ might not yet have enough information to deduce the distance between them; in this case, FJ apologizes profusely and replies with "-1".

Input

* Line 1: Two space-separated integers: N and M



* Lines 2..M+1: Each line contains four space-separated entities, F1,

        F2, L, and D that describe a road. F1 and F2 are numbers of

        two farms connected by a road, L is its length, and D is a

        character that is either 'N', 'E', 'S', or 'W' giving the

        direction of the road from F1 to F2.



* Line M+2: A single integer, K (1 <= K <= 10,000), the number of FB's

        queries



* Lines M+3..M+K+2: Each line corresponds to a query from Farmer Bob

        and contains three space-separated integers: F1, F2, and I. F1

        and F2 are numbers of the two farms in the query and I is the

        index (1 <= I <= M) in the data after which Bob asks the

        query. Data index 1 is on line 2 of the input data, and so on.

Output

* Lines 1..K: One integer per line, the response to each of Bob's

        queries.  Each line should contain either a distance

        measurement or -1, if it is impossible to determine the

        appropriate distance.

Sample Input

7 6
1 6 13 E
6 3 9 E
3 5 7 S
4 1 3 N
2 4 20 W
4 7 2 S
3
1 6 1
1 4 3
2 6 6

Sample Output

13
-1
10

Hint

At time 1, FJ knows the distance between 1 and 6 is 13.
At time 3, the distance between 1 and 4 is still unknown.
At the end, location 6 is 3 units west and 7 north of 2, so the distance is 10.

Source

USACO 2004 February

题目链接：http://poj.org/problem?id=1984

题目大意：在一个图中，只有上下左右四个方向的边。给出这样的一些边，求任意2个节点之间的曼哈顿距离。

题目分析：代权并查集，由于要根据时间来判断当前状态，又题目说了查询时间是递增的，我们不妨先把输入的信息存储下来，根据查询的时间来将信息加入集合中，设定两个数组x[i],y[i]分别表示i点相对于原点（这里的原点即我们设定的根结点）的横坐标和纵坐标，方向就同二维坐标系一样，通过方向来改变坐标值，压缩路径时要更新w[i]的值，合并的过程和CD题相同，采用向量法。
r1->r2 = r1->a + a->b + b->r2，因为w[i]表示i对原点的偏移量，所以w[r2] = w[a] + d -w[b]，若两点在同一集合中直接计算出其曼哈顿距离，若两点不在同一集合中，说明不连通，则输出－1
模拟一遍样例，这里是执行完Find(1-7)以后的坐标
t = 1:   x[1] = 0，   y[1] = 0
           x[6] = 13， y[6] = 0

t = 2:   x[1] = 0，   y[1] = 0
           x[6] = 13， y[6] = 0
           x[3] = 22， y[3] = 0

t = 3:   x[1] = 0，   y[1] = 0
           x[6] = 13， y[6] = 0
           x[3] = 22， y[3] = 0
           x[5] = 22， y[5] = -7

t = 4(换原点)：
           x[4] = 0，   y[4] = 0
           x[1] = 0，   y[1] = 3
           x[6] = 13， y[6] = 3
           x[3] = 22， y[3] = 3
           x[5] = 22， y[5] = -4

t = 5(换原点)：
           x[2] = 0，   y[2] = 0
           x[4] = -20，y[4] = 0
           x[1] = -20，y[1] = 3
           x[6] = -7，  y[6] = 3
           x[3] = 2，   y[3] = 3
           x[5] = 2，   y[5] = -4

t = 6:   x[2] = 0，   y[2] = 0
           x[4] = -20，y[4] = 0
           x[1] = -20，y[1] = 3
           x[6] = -7，  y[6] = 3
           x[3] = 2，   y[3] = 3
           x[5] = 2，   y[5] = -4
           x[7] = -20，y[7] = -2

#include 
#include 
int const MAX = 40005;
int fa[MAX], x[MAX], y[MAX];
int n, m, k;
char get[MAX][50];

void UF_set()
{
    for(int i = 0; i <= n; i++)
    {
        fa[i] = i;
        x[i] = y[i] = 0;
    }
}

int Find(int nd)
{
    if(nd == fa[nd])
        return nd;
    int tmp = fa[nd];
    fa[nd] = Find(fa[nd]);
    x[nd] += x[tmp];
    y[nd] += y[tmp];
    return fa[nd];
}

void Union(int a, int b, int dx, int dy)
{
    int r1 = Find(a);
    int r2 = Find(b);
    if(r1 != r2)
    {
        fa[r2] = r1;
        x[r2] = x[a] + dx - x[b];
        y[r2] = y[a] + dy - y[b]; 
    }
}

int abs(int a)
{
    return a > 0 ? a : -a;
}

int dis(int x1, int x2, int y1, int y2)
{
    return abs(x1 - x2) + abs(y1 - y2);
}

int main()
{
    scanf("%d %d", &n, &m);
    UF_set();
    getchar();
    for(int i = 0; i < m; i++)
        gets(get[i]);
    scanf("%d", &k);
    int nd1, nd2, ct, cur = 0;
    while(k--)
    {
        int a, b, d;
        scanf("%d %d %d", &nd1, &nd2, &ct);
        for(int i = cur; i < ct; i++)
        {
            int dx = 0, dy = 0;
            char dir[2];
            sscanf(get[i], "%d %d %d %s", &a, &b, &d, dir);
            switch(dir[0])
            {
                case 'E': dx += d; break;
                case 'W': dx -= d; break;
                case 'N': dy += d; break;
                case 'S': dy -= d; break;
            }
            Union(a, b, dx, dy);
        }
        cur = ct;
        //这两步很重要，不只是找到r1和r2的根，还更新了x[],y[],同G题
        int r1 = Find(nd1);
        int r2 = Find(nd2);
        if(r1 != r2)
            printf("-1\n");
        else
            printf("%d\n", dis(x[nd1], x[nd2], y[nd1], y[nd2]));
    }
}

G题 Cube Stacking

Time Limit: 2000MS		Memory Limit: 30000K
Total Submissions: 19686		Accepted: 6888
Case Time Limit: 1000MS

Description

Farmer John and Betsy are playing a game with N (1 <= N <= 30,000)identical cubes labeled 1 through N. They start with N stacks, each containing a single cube. Farmer John asks Betsy to perform P (1<= P <= 100,000) operation. There are two types of operations:
moves and counts.
* In a move operation, Farmer John asks Bessie to move the stack containing cube X on top of the stack containing cube Y.
* In a count operation, Farmer John asks Bessie to count the number of cubes on the stack with cube X that are under the cube X and report that value.

Write a program that can verify the results of the game.

Input

* Line 1: A single integer, P

* Lines 2..P+1: Each of these lines describes a legal operation. Line 2 describes the first operation, etc. Each line begins with a 'M' for a move operation or a 'C' for a count operation. For move operations, the line also contains two integers: X and Y.For count operations, the line also contains a single integer: X.

Note that the value for N does not appear in the input file. No move operation will request a move a stack onto itself.

Output

Print the output from each of the count operations in the same order as the input file.

Sample Input

6
M 1 6
C 1
M 2 4
M 2 6
C 3
C 4

Sample Output

1
0
2

Source

USACO 2004 U S Open

题目链接：http://poj.org/problem?id=1988

题目大意：有n个操作，M a b相当于把编号为a的盘子放到编号为b的上面，注意这里不是插放，是把编号为a的那堆放在编号为b的那一堆的最上面

C a表示询问a下面有几个盘子

题目分析：带权并查集，把b当作a的根，需要三个数组fa[x]表示x的祖先，w[x]表示x到根的距离，cnt[x]表示已x为根的当前堆的数量，我们只需要不断维护w[]和cnt[]两个数组下面给出一组样例和程序执行的过程

7
M 1 6
M 2 4
M 2 6
C 2
M 5 7
M 5 6
C 5

r1 = Find(1) = 1；r2 = Find(6) = 6；（此时w[1] = 0，w[6] = 0）；

fa[1] = 6（6为1的祖先）； w[1] = cnt[6] = 1（1下面有1个，即6）；

cnt[6] = cnt[1] + cnt[6] = 2（已6为根的堆的数量为2，即1和6）；

r1 = Find(2) = 2；r2 = Find(4) = 4； （此时w[2] = 0，w[4] = 0）；

fa[2] = 4（4为2的祖先）； w[2] = cnt[4] = 1（2下面有1个，即4）；

cnt[4] = cnt[4] + cnt[2] = 2（已4为根的堆的数量为2，即2和4）；

r1 = Find(2) = 4(第二步时得到2的祖先为4)；r2 = Find(6) = 6；fa[4] = 6（6为4的祖先）；（此时w[2] = w[2] + w[4] = 1）

w[4] = cnt[6] = 2（4下面有2个，即1，6）；

cnt[6] = cnt[6] + cnt[4] = 4（已6为根的堆的数量为4，即2,4,1,6）；

C2询问2下面有几个，这时w[2] = 2显然不对，因为w[2] = w[2] + w[4]之前Find的时候w[4]的值为0，可是Union完w[4] = 2因此我们要更新w[2]的值，更新的方法就是Find(2)就可以了，因为Find函数中，对于当前的x递归找它的祖先，加上其祖先下面的个数

r1 = Find(5) = 5；r2 = Find(7) = 7；  （此时w[5] = 0，w[7] = 0）；

fa[5] = 7（7为5的祖先）； w[5] = cnt[7] = 1 （5下面有1个，即7）；

cnt[7] = cnt[7] + cnt[5] = 2（已7为根的堆的数量为2，即5和7）；

r1 = Find(5) = 7；r2 = Find(6) = 6；  fa[7] = 6（6为7的祖先）； （此时w[5] = 1，w[7] = 0）

* w[7] = cnt[6] = 4 （7下面有4个，即2,4,1,6）；

cnt[6] = cnt[6] + cnt[7] = 6（已6为根的堆的数量为6，即5,7,2,4,1,6）；

C5询问5的下面有几个，显然5下面的个数为5到7的距离w[5] = 1加上7到6的距离w[7] = 4，这里我们必须Find(5)，因为在Find(5)之前w[5]还等于1，*号操作更新了w[7]，但没有更新w[5]，所以要更新w[5]。即Find(5)更新完之后w[5] = w[5] + w[7] = 5，我们看此时的序列为 5 7 2 4 1 6，5下面确实有5个。

#include 
int const MAX = 30005;
int fa[MAX], cnt[MAX], w[MAX];

void UF_set()
{
    for(int i = 1; i <= MAX; i++)
    {
        fa[i] = i;
        w[i] = 0;       //下面都没有，初始化为0
        cnt[i] = 1;     //当前堆只有自身，初始化为1
    }
}

int Find(int x)
{
    if(x == fa[x]) 
        return fa[x];
    int tmp = fa[x];
    fa[x] = Find(fa[x]);
    w[x] += w[tmp];
    return fa[x];
}

void Union(int a, int b)
{
    int r1 = Find(a);
    int r2 = Find(b);
    if(r1 != r2) 
    {
        fa[r1] = r2;
        w[r1] = cnt[r2]; //r1下面的个数为r2的堆数
        cnt[r2] += cnt[r1]; //r2的堆数要加上r1那堆的数量
    }
}

int main()
{
    int T, x, y;
    char s[2];
    scanf("%d", &T);
    UF_set();
    while(T--)
    {
        scanf("%s", s);
        if(s[0] == 'M')
        {
            scanf("%d %d", &x, &y);
            Union(x, y);
        }
        else
        {
            scanf("%d", &x);
            //这里一定要在Find函数中更新一次w[x]的值
            //可以通过样例4 M 1 6 M 2 4 M 2 6 C 2看出来
            Find(x);
            printf("%d\n", w[x]);
        }
    }
}

H题 Wireless Network

Time Limit: 10000MS		Memory Limit: 65536K
Total Submissions: 17156		Accepted: 7214

Description

An earthquake takes place in Southeast Asia. The ACM (Asia Cooperated Medical team) have set up a wireless network with the lap computers, but an unexpected aftershock attacked, all computers in the network were all broken. The computers are repaired one by one, and the network gradually began to work again. Because of the hardware restricts, each computer can only directly communicate with the computers that are not farther than d meters from it. But every computer can be regarded as the intermediary of the communication between two other computers, that is to say computer A and computer B can communicate if computer A and computer B can communicate directly or there is a computer C that can communicate with both A and B.

In the process of repairing the network, workers can take two kinds of operations at every moment, repairing a computer, or testing if two computers can communicate. Your job is to answer all the testing operations.

Input

The first line contains two integers N and d (1 <= N <= 1001, 0 <= d <= 20000). Here N is the number of computers, which are numbered from 1 to N, and D is the maximum distance two computers can communicate directly. In the next N lines, each contains two integers xi, yi (0 <= xi, yi <= 10000), which is the coordinate of N computers. From the (N+1)-th line to the end of input, there are operations, which are carried out one by one. Each line contains an operation in one of following two formats:
1. "O p" (1 <= p <= N), which means repairing computer p.
2. "S p q" (1 <= p, q <= N), which means testing whether computer p and q can communicate.

The input will not exceed 300000 lines.

Output

For each Testing operation, print "SUCCESS" if the two computers can communicate, or "FAIL" if not.

Sample Input

4 1
0 1
0 2
0 3
0 4
O 1
O 2
O 4
S 1 4
O 3
S 1 4

Sample Output

FAIL
SUCCESS

Source

POJ Monthly,HQM

题目链接：http://poj.org/problem?id=2236

题目大意：有n台损坏的电脑，每两台之间可以通信的最大距离为d，给出n台电脑的坐标，两个操作，O x表示修复第x台

S x y表示询问x与y间能否访问。

题目分析：水题，修复了的标记一下，根据d的条件把能通信的放在一个集合里面，询问时如果根相同说明可以通信

#include 
#include 
int const MAX = 1005;
int fa[MAX], ok[MAX];
int n, d;

struct Point
{
    int x, y;
    int id;
}p[1005];

void UF_set()
{
    for(int i = 1; i <= n; i++)
        fa[i] = i;
}

int Find(int x)
{
    return x == fa[x] ? x : fa[x] = Find(fa[x]);
}

void Union(int a, int b)
{
    int r1 = Find(a);
    int r2 = Find(b);
    if(r1 != r2)
        fa[r2] = r1;
}

int dis(int x1, int y1, int x2, int y2)
{
    return (x1 - x2) * (x1 - x2) + (y1 - y2) * (y1 - y2);
}

int main()
{
    memset(ok, 0, sizeof(ok));
    scanf("%d %d", &n, &d);
    UF_set();
    for(int i = 1; i <= n; i++)
 {
        scanf("%d %d", &p[i].x, &p[i].y);
        p[i].id = i;
    }
    char s[2];
    bool tmp = false;
    int x, y;
    while(scanf("%s %d", s, &x) != EOF)
    {
        if(s[0] == 'O')
        {
            ok[p[x].id] = 1;
            for(int i = 1; i <= n; i++)
                if(dis(p[x].x, p[x].y, p[i].x, p[i].y) <= (d * d) && ok[p[i].id])
                    Union(x, i);
        }
        else
        {
            scanf("%d", &y);
            if(Find(x) == Find(y))
                printf("SUCCESS\n");
            else
                printf("FAIL\n");
        }
    }
}

I题 Supermarket

Time Limit: 2000MS		Memory Limit: 65536K
Total Submissions: 9422		Accepted: 4056

Description

A supermarket has a set Prod of products on sale. It earns a profit px for each product x∈Prod sold by a deadline dx that is measured as an integral number of time units starting from the moment the sale begins. Each product takes precisely one unit of time for being sold. A selling schedule is an ordered subset of products Sell ≤ Prod such that the selling of each product x∈Sell, according to the ordering of Sell, completes before the deadline dx or just when dx expires. The profit of the selling schedule is Profit(Sell)=Σ_x∈Sellpx. An optimal selling schedule is a schedule with a maximum profit.
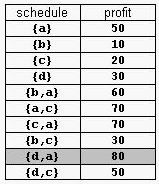
For example, consider the products Prod={a,b,c,d} with (pa,da)=(50,2), (pb,db)=(10,1), (pc,dc)=(20,2), and (pd,dd)=(30,1). The possible selling schedules are listed in table 1. For instance, the schedule Sell={d,a} shows that the selling of product d starts at time 0 and ends at time 1, while the selling of product a starts at time 1 and ends at time 2. Each of these products is sold by its deadline. Sell is the optimal schedule and its profit is 80.

Write a program that reads sets of products from an input text file and computes the profit of an optimal selling schedule for each set of products.

Input

A set of products starts with an integer 0 <= n <= 10000, which is the number of products in the set, and continues with n pairs pi di of integers, 1 <= pi <= 10000 and 1 <= di <= 10000, that designate the profit and the selling deadline of the i-th product. White spaces can occur freely in input. Input data terminate with an end of file and are guaranteed correct.

Output

For each set of products, the program prints on the standard output the profit of an optimal selling schedule for the set. Each result is printed from the beginning of a separate line.

Sample Input

4  50 2  10 1   20 2   30 1

7  20 1   2 1   10 3  100 2   8 2
   5 20  50 10

Sample Output

80
185

Hint

The sample input contains two product sets. The first set encodes the products from table 1. The second set is for 7 products. The profit of an optimal schedule for these products is 185.

Source

Southeastern Europe 2003

题目链接：http://poj.org/problem?id=1456

题目大意：有n种商品，每种商品有个价值和其最晚卖出时间，每个商品要卖一天，问怎样设置出售计划可使利润最高，求最高利润

题目分析：本题是并查集神用，但是是用来优化，这题目贪心的思路很明确，先按照价值从大到小排序，如果当前天没有被别的商品占有则该商品就在这天卖，否则在前一天卖，若一直推到第一天都被占有，则放弃该商品，因为价值已经按从大到小排过序，放弃不会使总利润降低。关键是并查集的优化部分，如果当前天没有被占，则将当前天和前一天合并，这里必须把前一天当作祖先，即
fa[cur] = pre。因为这里找某商品在第几天出售实际上是用了路经压缩的思想，比如一个商品排完序后在第四天出售，则将第三天做为第四天的祖先，下次Find(4)的时候相当于找4的祖先即3，以此类推，我们来分析一下这里用路经压缩和不用的时间复杂度
如果不用那时间复杂度就是O(n^2)，你要从当前天数开始往前枚举
如果用路径压缩Unoin操作O(1)，Find操作在不成链的情况下，平均O(logn)，所以总的复杂度为O(nlogn)，相对O(n^2)快很多

#include 
#include 
using namespace std;
int const MAX = 1e4 + 5;
int n, ans;
int fa[MAX];

struct PRODUCTS
{
    int p, d;
}pr[MAX];

void UF_set()
{
    for(int i = 0; i < MAX; i++)
        fa[i] = i;
}

int Find(int x)
{
    return x == fa[x] ? x : fa[x] = Find(fa[x]);  
}

void Union(int a, int b)
{
    int r1 = Find(a);
    int r2 = Find(b);
    if(r1 != r2)
        fa[r1] = r2; //这里不能反，必须把前一天做为当前天的根
}

int cmp(PRODUCTS a, PRODUCTS b)
{
    return a.p > b.p;
}

int main()
{
    while(scanf("%d", &n) != EOF)
    {
        UF_set();
        ans = 0;
        for(int i = 0; i < n; i++)
            scanf("%d %d", &pr[i].p, &pr[i].d);
        sort(pr, pr + n, cmp);
        for(int i = 0; i < n; i++)
        {
            int curpos = Find(pr[i].d);
            if(curpos)
            {
                ans += pr[i].p;
                Union(curpos, curpos - 1);
            }
        }
        printf("%d\n", ans);
    }
}