SVM——（四）目标函数求解

在之前的两篇文章中[1][2]分别用两种方法介绍了如何求得目标优化函数，这篇文章就来介绍如何用拉格朗日对偶(Lagrange duality)问题以及SMO算法求解这一目标函数，最终得到参数。

本文主要分为如下部分：
1.构造广义拉格朗日函数$\mathcal{L}(w,b,\alpha )$
2.关于参数$w,b$,求$\mathcal{L}$的极小值$W(\alpha )$
3.使用SMO算法求$W(\alpha )$的极大值
4.求解参数$w,b$
其中2,3,4也是求解对偶问题的一般步骤。

1.构造广义拉格朗日函数$\mathcal{L}(w,b,\alpha )$

由上文可知SVM最终的优化目标为：

$$\begin{array}{l}{\min }_{\mathbf{\omega },b}\frac{1}{2}||\mathbf{\omega }|{|}^2\\ \\ \text{s. t.}{y}_i({\mathbf{\omega }}^T{\mathbf{x}}_i+b)\ge 1,i=1,2,...,m\end{array}\text{\hspace{1em}(1.1)}$$

由此我们可以得到广义的拉格朗日函数为：

$\mathbf{G}\mathbf{e}\mathbf{n}\mathbf{e}\mathbf{r}\mathbf{a}\mathbf{l}\mathbf{i}\mathbf{z}\mathbf{e}\mathbf{d}\mathbf{L}\mathbf{a}\mathbf{g}\mathbf{r}\mathbf{a}\mathbf{n}\mathbf{g}\mathbf{i}\mathbf{a}\mathbf{n}$
$$\begin{array}{rl}& \mathcal{L}(w,b,\alpha )=\frac{1}{2}||w|{|}^2-\sum _{i=1}^m{\alpha }_i[y^{(i)}(w^T{x}^{(i)}+b)-1]\\ & s.t.g_i(w)=-y^{(i)}(w^T{x}^{(i)}+b)+1\le 0\end{array}\text{\hspace{1em}(1.2)}$$

注：此处有两个参数$w,b$,一个拉格朗日乘子向量$\alpha$，且${\alpha }_i\ge 0$，因为只有这样才能满足$\frac{1}{2}||w|{|}^2=\max \mathcal{L}$；(详见此处)

由对偶性：
$$d^{\ast }=\underset{\alpha ,{\alpha }_i\ge 0}{\max }\underset{w,b}{\min }\mathcal{L}(w,b,\alpha )=\underset{w,b}{\min }\underset{\alpha ,{\alpha }_i\ge 0}{\max }\mathcal{L}(\omega ,\alpha ,\beta )=p^{\ast }\text{\hspace{1em}(1.3)}$$
可知，对偶问题$d^{\ast }$与原始问题$p^{\ast }$同解，但上述过程需满足KKT条件：
$$\begin{array}{r}\{\begin{array}{l}{\alpha }_i\ge 0;\\ g_i(w,b)\le 0;\\ {\alpha }_i{g}_i(w,b)=0\end{array}\end{array}\text{\hspace{1em}(1.4)}$$

于是，对于任意训练样本$(x^{(i)},y^{(i)})$，总有${\alpha }_i=0$或者${\alpha }_i{g}_i(w,b)=0$。若${\alpha }_i=0$，由下面$(2.1)$可知，超平面为$0x+b=0$，这就意味着与决策面与该样本点无关；若${\alpha }_i>0$，则必有$y^{(i)}(w^T{x}^{(i)}+b)=1$，也就是说该样本点是一个支持向量。这显示出一个重要性质：超平面仅仅与支持向量有关。

2.关于参数$w,b$,求$\mathcal{L}$的极小值$W(\alpha )$

这一步同拉格朗日乘数法求极值一样，分别对$w,b$求偏导，并令其为0：
$$\begin{array}{rl}\frac{\partial \mathcal{L}}{\partial w}& =w-\sum _{i=1}^m{\alpha }_i{y}^{(i)}{x}^{(i)}=0\\ w& =\sum _{i=1}^m{\alpha }_i{y}^{(i)}{x}^{(i)}\end{array}\text{\hspace{1em}(2.1)}$$

$$\begin{array}{rl}\frac{\partial \mathcal{L}}{\partial b}& =\sum _{i=1}^m{\alpha }_i{y}^{(i)}=0\end{array}\text{\hspace{1em}(2.2)}$$
常用范数求导法则
将$(2.1),(2.2)$代入$(1.2)$可知：

$$\begin{array}{r}W(\alpha )=\underset{w,b}{\min }\mathcal{L}(w,b,\alpha )=\sum _{i=1}^m{\alpha }_i-\frac{1}{2}\sum _{i,j=1}^m{y}^{(i)}{y}^{(j)}{\alpha }_i{\alpha }_j(x^{(i)}{)}^T{x}^{(j)}\end{array}\text{\hspace{1em}(2.3)}$$

详细步骤：
$$\begin{array}{rl}\mathcal{L}& =\frac{1}{2}{w}^{T}w-\sum _{i=1}^m{\alpha }_i[y^{(i)}(w^T{x}^{(i)}+b)-1]\\ & =\frac{1}{2}{w}^{T}w-\sum _{i=1}^m{\alpha }_i{y}^{(i)}{w}^T{x}^{(i)}-\sum _{i=1}^m{\alpha }_i{y}^{(i)}b+\sum _{i=1}^m{\alpha }_i\\ & =\frac{1}{2}{w}^{T}w-w^T\sum _{i=1}^m{\alpha }_i{y}^{(i)}{x}^{(i)}-b\sum _{i=1}^m{\alpha }_i{y}^{(i)}+\sum _{i=1}^m{\alpha }_i\\ & \text{代入(2.1)(2.2)}得\\ W(\alpha )& =\frac{1}{2}{w}^{T}w-w^{T}w+\sum _{i=1}^m{\alpha }_i\\ & =\sum _{i=1}^m{\alpha }_i-\frac{1}{2}{w}^{T}w\\ & =\sum _{i=1}^m{\alpha }_i-\frac{1}{2}\sum _{i,j=1}^m{\alpha }_i{\alpha }_j{y}^{(i)}{y}^{(j)}(x^{(i)}{)}^T{x}^{(j)}\\ \text{其中：}{w}^{T}w& =\sum _{i=1}^m{\alpha }_i{y}^{(i)}{x}^{(i)}\cdot \sum _{j=1}^m{\alpha }_j{y}^{(j)}{x}^{(j)}\\ & =\sum _{i,j=1}^m{\alpha }_i{\alpha }_j{y}^{(i)}{y}^{(j)}(x^{(i)}{)}^T{x}^{(j)}\\ & =\sum _{i=1}^m\sum _{j=1}^m{\alpha }_i{\alpha }_j{y}^{(i)}{y}^{(j)}(x^{(i)}{)}^T{x}^{(j)}\end{array}$$

3.使用SMO算法求$W(\alpha )$的极大值

由(2.3)我们可以得出如下优化问题：
$$\begin{array}{rl}\underset{\alpha }{\max }& W(\alpha )=\sum _{i=1}^m{\alpha }_i-\frac{1}{2}\sum _{i,j=1}^m{y}^{(i)}{y}^{(j)}{\alpha }_i{\alpha }_j(x^{(i)}{)}^T{x}^{(j)}\\ s.t.& {\alpha }_i\ge 0,i=1,...,m\\ & \sum _{i=1}^m{\alpha }_i{y}^{(i)}=0\end{array}\text{\hspace{1em}(3.1)}$$
之所以$(2.2)$也会成为约束条件，是因为$W(\alpha )$就是通过$(2.2)$求解的出来的，是$W(\alpha )$存在的前提。

现在我们的优化问题变成了如上的形式。对于这个问题，我们有更高效的优化算法，即序列最小优化（SMO）算法。我们通过这个优化算法能得到α，再根据α，我们就可以求解出w和b，进而求得我们最初的目的：找到超平面，即”决策平面”。

至于具体求解步骤，不急咱们先放着，到后面再来解决。

总结一句话：我们为啥使出吃奶的劲儿进行推导？因为我们要将最初的原始问题，转换到可以使用SMO算法求解的问题，这是一种最流行的求解方法。为啥用这种求解方法？因为它牛逼啊！

4. 求解$w,b$

经过3.2求解出$\alpha$之后，代入$(18)$即可求解出$w$;而b的求解公式为：
$$b=-\frac{1}{2}(\underset{i:y^{(i)}=-1}{\max }{w}^T{x}^{(i)}+\underset{i:y^{(i)}=+1}{\min }{w}^T{x}^{(i)})$$

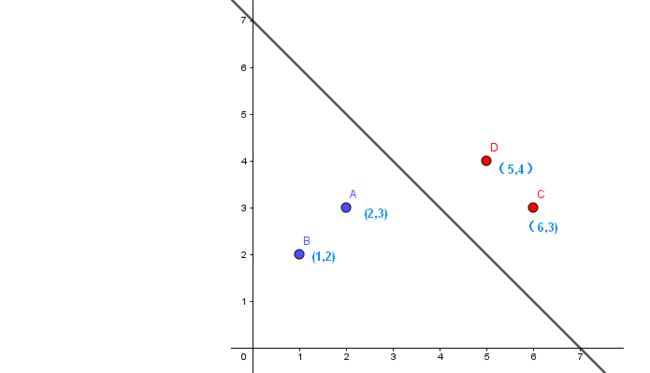
例如：

如图，红色为正样本($y=+1$),紫色为负样本($y=-1$),直线为$x_1+x_2-b=0$,则有：

$$\begin{array}{rl}& \underset{i:y^{(i)}=-1}{\max }{w}^T{x}^{(i)}=\max (1\ast 2+1\ast 3,1\ast 1+1\ast 2)=5\\ & \underset{i:y^{(i)}=+1}{\min }{w}^T{x}^{(i)}=\min (1\ast 5+1\ast 4,1\ast 6+1\ast 3)=9\\ & b=-\frac{1}{2}(5+9)=-7\end{array}$$

SVM——（七）SMO（序列最小最优算法）
SVM——（六）软间隔目标函数求解
SVM——（五）线性不可分之核函数
SVM——（四）目标函数求解
SVM——（三）对偶性和KKT条件（Lagrange duality and KKT condition）
SVM——（二）线性可分之目标函数推导方法2
SVM——（一）线性可分之目标函数推导方法1

参考：

• Python3《机器学习实战》学习笔记（八）：支持向量机原理篇之手撕线性SVM
• 《机器学习》周志华