无法理解高等数学怎么办?
我大学四年都没理解高等数学,这是博士毕业之后的理解。
一、我的数学学习历程及遇到的困难
1、我的数学学习历程
我个人的数学学习历程比较曲折,在大一的时候挂过数学分析。我本科是学工程的,所以我们大一的数学课跟数学系的课程几乎是一致的。
大二的时候还挂过高等代数。
两次考研,第一次考研没考上,第二次考研成功了,我考上了理想的学校,理想的专业,选择了理想的导师,以专业第一名的成绩录取,包括专业课的成绩也是第一名。
当然,数学学习的历程比较曲折,有很多原因。
一方面是个人兴趣的原因。在大学的时候,一进图书馆看到很多的学问,立刻就对各种各样的学问都产生了很浓厚的兴趣,所以精力比较分散,这是一方面的客观原因。
主观原因是大学的数学一直没有入门,大学的数学,高等数学,线性代数,数学分析还有概率统计等等这些课,跟高中的数学内容有很大的差别。我高中的数学成绩起初一般,也可以说很差(取决于标准。因为高二下还考过不及格的分数),可是在大学(北京大学),数学却迟迟没入门。可以这么讲,今天看来,直到我大学二年级,甚至大学三、四年级,我的数学都没怎么入门。
那怎样入门呢?怎样才能学出数学的乐趣来,怎么能够快速的进步,这个就是今天我要分享主题。
2、数学学习过程中遇到的困难
在数学的学习过程中,到底会遇到什么样的困难?这些都是我个人经历过的。
第一是数学内容抽象,看不懂。
第二是知识点太多,记不住。
第三是题目太难,遇到难题不会做。
第四是找不到人讨论,太枯燥。
因为大学的学习特点,不像高中,大家都学一样的东西,然后按照同样的节奏在走,所以遇到同样的学科,还能讨论一下。可是大学呢,找人讨论都很困难,各忙各的,所以就显得这个学习过程很枯燥。
第五是战线太长,导致很难坚持。
什么叫战线太长?我们大学的数学一般会学两年。像我那时候学数学分析要学一年半,三个学期的课程,一旦不入门的话,那就很难坚持学下去,越学越难受。
第六是时间太短,压力大。
怎么时间又太短了呢?因为隔两个月就期中考试啊,再隔两个月就期末考试。等到复习的时候,准备考试的时候又觉得压力很大了。
有个朋友说,“眼睁睁看着老师把一道全是英文和希腊字母的题,最后解出的答案竟然是阿拉伯数字,直到现在还费解。”这些实际上是指高等数学比较抽象。
二、对数学学习的反思
1、令人费解的数学名言
在我大一、大二的时候也看了不少这样的类似的名言,感觉到写得非常的优美,但是几乎体验不到这里面说的任何一句话的含义。所以当时就觉得很着急,难道这么好的东西,我跟它无缘吗?
同样,另外一种情形,更让人无奈。就是这些所谓的学霸和大神们,我称之为令人绝望的人。比如说我有一个同学,也是我师弟,我们在讨论数学的时候,经常我们在黑板上写一道微积题目在黑板上算,他站在远处,看了30秒钟,直接报一个答案。这样的人有时在我身边,有时候我们在网上看到。当然就觉得不可理喻,这样的人难道说天生就具有数学头脑吗?我们就不行吗?我就不行吗?等等。在整个大一、大二,甚至大三都在这样的困惑中在啃着数学。
2、数学到底是什么?
本科时的这样一个经历,再加之后面的考研,让我重新再反思:
数学到底是什么?我们应该如何来学习数学?这个过程中有几件事给我的印象比较深刻。
一个是去阅读那些数学的名著,看这些数学家们到底是怎么看数学,怎么看数学的学习的。
二是参加了我们学校BBS上面一个科学版的活动,在科学版上跟同学们讨论问题,而且还有线下的面对面的讨论,一个月有一次这样的活动。这两类活动给我很大的启发,关于什么是学问?学问的本质究竟是什么?
今天看来,那个时候得出的认识是这样的,学问的本质是人与知识,人与人,人与自己的对话,当我们进入了对话的进程,我们就入门了。大家看看这段话是不是有道理?
三、数学是什么?
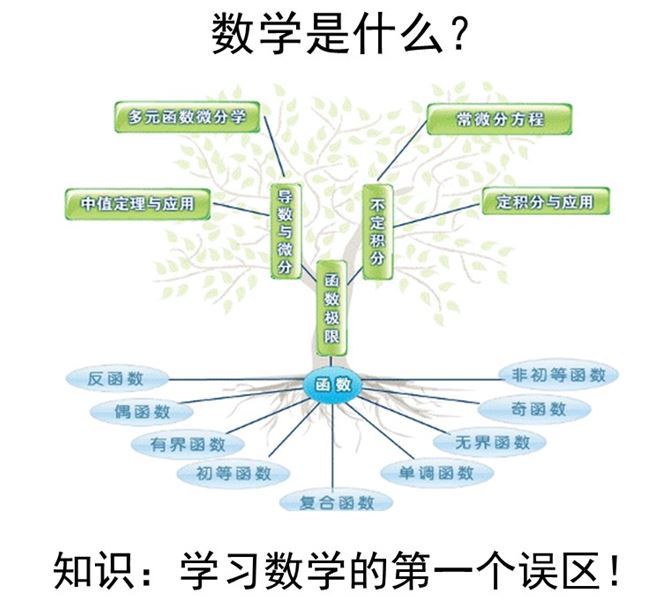
要读懂高等数学,我们必然会问这样一个问题,数学究竟是什么?以高等数学为例,大家在网上常常会看到这样的所谓知识结构图。
在这副图里面,把高等数学比喻成一棵大树,函数是这棵大树的根,我们高中的数学里面都已经学过了,如反函数、奇偶函数的奇偶性、初等函数、复合函数等等;然后这棵大树的主干是函数的极限,也就是我们高等数学的第一章,函数的极限。
在左边,函数的极限生长出一个大的分支,叫做导数与微分。导数与微分首先涉及到中值定理,微分中值定理和中值定理的应用。然后它又导向了第二个分支,多元函数的微分学,而函数的极限又引出了另外一个大的分支,叫做不定积分,不定积分一方面,引向定积分与定积分的应用,另一方面又引向了常微分方程。这不是思维导图做的,这就是直接在这棵大树上面加上去的一些,用PPT就可以做出来。
像这样的图像对大家把握一门知识是有利的,但这样的图片也会造成一个误导。导致我们把数学仅仅当做知识来看待。因此产生了数学学习的巨大的困难和障碍。我称之为这就是把数学仅仅当做知识来看待,它是学习数学的第一个误区。
我们看看大数学家们是怎么看数学的。比如这本书叫做《什么是数学》,副标题是“对思想和方法的基本研究”,它的作者是柯朗。柯朗是20世纪最伟大的数学家之一,美国有一个世界闻名的柯朗研究所。很多大科学家对这本书有高度的赞誉,比如爱因斯坦说,“本书是对整个数学领域中的基本概念及方法的透彻清晰的阐述”;爱因斯坦的好朋友,韦尔是20世纪伟大的数学物理学家,他称赞,“这是一本非常完美的著作,被数学家们视作科学的鲜血的一切基本思路和方法。在《什么是数学》这本书中,用最简单的例子,使之清晰明了,已经达到了令人惊讶的程度”。
看到爱因斯坦和韦尔评价这本书的话,我们都很想去读一读这本书究竟在讲什么,但是如果大家去看这本书,多数人会感到失望,包括我在本科三、四年级的时候,去看这本书的时候,倍感失望。因为这本书里面讲的有三章的内容跟我们的高等数学的内容是一样的,里面有重合的部分,比如这里面涉及到极限,微分和积分。
为什么会失望呢?是因为这本书里面进的东西,我们看起来似乎很简单,比我们教科书的内容还要简单一些。那为什么这样一本书会受到如此高度的赞誉?后来我花了好几年的时间琢磨,得到这么一个答案。实际上这本书看似内容并不复杂,但是它却告诉了我们一件事,那就是数学究竟是什么?它的答案就是:数学的本质是思维技能!
我们看一看,高等数学的所有部分都贯穿着同样的思维结构。
这个思维结构是什么?
就是从问题引入定义,这个定义一般会对应着几何直观;然后定义又引入定义的性质,比如导数的性质,极限的性质等,另外,定义包含着运算,比如导数,从导数的定义直接就可以推出运算法则。然后从定义和运算法则和性质,会推出一系列的定理,这些定理在各个复杂的数学情形中进行应用,乃至应用于其他的领域,包括物理学,经济学,生物学等等。
大家注意,这里关键在于所有的数学分支都是这么同样的一个结构,几乎是完全相同的,大家看看这个说法是不是有道理,大家回忆一下,是不是高数的所有分支都是这样一个同样的结构。
如果我们把高等数学的本质当做思维技能来看待,我们立即能回答很多问题,比如说为什么平时做题不错,而考研成绩却不佳,其实最重要的原因是把数学仅仅当做知识来学,因为考研的时候,就它不会考同样的题目。题型还会变动,我们的记忆是会波动的,如果我们着眼于这个思维技能,我们就会发现,技能比知识的记忆要稳定得多,技能比知识的记忆要快得多,技能往往是一种自动化的东西,而知识需要想半天。
我们从一个正面的例子来看,有一位师弟,他在考研过程中感冒,前两科就感冒,考到数学的时候还感冒,结果他数学还是考了143分,考的是数学一,他用的参考书全是2013版的,本来是2014年考研,应该用2014年版的参考书,但是他用的2013版的。为什么他能够做到这一点,实际上数学在他大脑中,变成了这个思维的技能。
可能很多人仍然不理解:数学知识和数学的思维技能究竟有什么差别?
举一个例子,看过一万遍钢琴谱的人会弹钢琴吗?甚至弹过一万遍1234567的人,能弹好曲子吗?显然不一定啊。所以当我们去学数学的时候,我们看许多遍书,不一定有效。看许多遍视频,也不一定有效,即便是练过许多题目,也不一定有效,因为这么做的人多了,考的成绩不理想的。这么做的人,考的成绩不理想的人,比比皆是。
那么什么才是核心?什么才是关键?
最核心的是训练数学的思维。当我们看书的时候,当我们看视频的时候,当我们练习题目的时候,如果我们关注的是如何训练自己的数学思维,这样才会产生效果。这种训练会训练出一种思维技能,数学的思维技能,而这种技能是贯穿于数学的所有分支,所有部分的。
这种技能甚至还可以迁移到其他领域,如果我们把数学看作思维技能的话,立刻可以理解为什么数学成绩很突出的人,反而不去记很多东西?就像我刚才讲的那位师弟,在黑板上出一道积分的题目,我们来出题,我们在那讨论,他站在那30秒钟直接报了个答案。他就是这种类型的人,他不会记很多的数学知识,但他却能迅速解题。为什么?因为他们必要的时候可以推导出来,把公式推导出来,这些知识在他们大脑中是一个有机的记忆,甚至是自动化的。
那么数学思维的精髓究竟是什么?
这张图片给了我关于这个答案的深刻的启发,这张图片是我读研究生的时候,在一个关于力学的国际研讨会上,有一位学者,第一张幻灯片就播放的是这张图片。这张图片就几个要素,首先最核心肯定是坐在椅子上这位学者,周围是书籍,各种书籍,实验仪器等等,很郁闷。旁边两位学者在窃窃私语,下面这句话讲的是:“After twendy years of research. Quimzy develeped the answer…now he’s forgotten the question.”也就是说:Quimzy研究了二十年,找到了答案,却忘记了问题!
这三行小字,当我第一次读到的时候,对我是一个强烈的震撼。因为我终于找到答案了。它道出了:学问的本质,数学的本质是什么?这个本质就是:问答。他虽然研究了二十多年,搞了很多的成果,所谓的成果,但是他却陷入了困惑,为什么陷入困惑?因为他不知道他得出的这些结果,究竟能回答什么问题。这就像我们学习高等数学是一样的,我们在整天做题目,看书,可是我们看到脑子里面这些东西,究竟能回答什么问题。越来越模糊了,那么于是就陷入了困惑,甚至进入了数学学习的困惑。
爱因斯坦在《物理学的进化》开篇就讲,“提出一个问题,往往比解决一个问题更为重要,因为解决一个问题,也许是一个数学上或实验上的技巧,而提出新的问题,新的可能性,从新的角度看旧问题,却需要创造性的想象力,而且标志着科学的真正进步。”
这段话用来描述我们数学学习的过程,同样恰当。我们可以这么说,在数学的学习历程中,提出一个问题往往比解决一个问题更为重要,因为解决一个问题,也许是一个数学上的技巧,而提出新的问题,新的可能性,从新的角度看旧问题,却需要创造性的想象力,而且标志着数学学习的真正进步。
康托,20世纪最伟大的数学家之一,集合论的创始人,他说了这么一句话,“在数学的领域中,提出问题的艺术,比解答的,解答问题的艺术更为重要。”
费曼的老师惠勒说过一句话,“没有问题,没有答案”。这句话道出了任何学问的本质,我们所有的学问,所有的知识,都是为了回答问题。但是如果没有问题的话,如果在我们的课本里面,在我们的学习过程中,没有提出这个问题,没有提出足够数量的问题,那么我们在脑袋里面堆积的那些东西都是学问的细枝末节,甚至是僵死的知识。
费曼的老师这么说,费曼也是同样的,费曼 20世纪最有名的物理学家之一。费曼在《别逗了,费曼先生》(实际上是个人传记)这本书里讲了他在巴西期间一个教学历程,在巴西的教学让他感到很头疼,如图片右边这段话,他说我无法推动他们做到的另一件事,是问问题。”“他们”,这里的“他们”就是指那些学生,那些大学生。“终于一个学生告诉我其中的原因,如果我在课堂上问你问题,之后大家都会跑来说,你为什么浪费大家的时间,我们的目的是学东西,但你却打断他,问他问题。”费曼对这个现象的评论是,“这是一种打压别人的坏风气,事实上大家全都不懂,但他们表现出一幅很懂的样子,以把别人比下去。”
四、数学学习的九个境界
数学精深训练有九个台阶。
第一个台阶是能看懂。
第二个台阶是能记住;
第三个台阶是会解题;
什么是能看懂?能看懂,就是能够懂得数学定义,定理,公式的来龙去脉。一看到这个定理、公式,脑子里面盘旋的一些问题,我们一一找到答案,我们要从内心里面去回答,那么找到的答案越多,做出来的问答越多,我们就懂得的越多,这就是能看懂的含义。
往往是这一步,使得很多人难以入门,一旦我们做到这一点的话,我们马上就迈上了第一个台阶,迈上第一个台阶之后,能记住会解题,只要我们把那些最基本的东西给做出来,做一遍,亲自动手去算一遍,那么我们马上就会跨过第二个、第三个台阶。
这样的话,考一个及格的分数就不成问题了。有不少人把高数的考研目标定为90分,实际上做完刚才所说的这些,每一章,每一节都这么去做的话,考90分根本不成问题。
第四个台阶是熟练解题;
在解题的过程中不断地进行这样的有意识的思维操作的训练,那么熟练解题也为之不远了。
第五个台阶是会梳理;
什么是会梳理?刚才已经给大家分享了数学的基本结构是什么?每一章都在重复同样的基本结构,把那些知识点都给汇总到这个知识结构里面,就是会梳理。包括我们每一章都在用什么样的运算技巧?大家心里面有没有数,这一章我们会用到什么,什么样的运算技巧,能不能1、2、3、4、5、6、7、8,这么列出来,一是一、二是二的列出来,如果这么做了,那肯定是会梳理了。
第六个台阶是融会贯通;
什么是融会贯通?比如导数,是从什么问题引入的?导数的定义,它的严格的定义是什么?它对应的几何直观是什么?导数怎么推出导数的四则运算法则?导数的定义和运算法则又有什么用?能解什么样的题目?如果我们一步步这么做下来的话,那就是融会贯通了,对这一章,这一节融汇贯通了。
第七个台阶是把握数学思维;
什么是把握数学思维?所谓的数学思维就是一个一个的基本的思维操作,像加、减、乘、除法,各种类型的加、减、乘、除法,像加一项、减一项,像它的定义,为什么会有这样的定义?它的问题是什么?这个定义能解决什么问题?当我们提这些问题,去找它的答案的时候,按照这样的思维去训练的时候,我们就把握数学思维了。
第八个台阶是体验学习的乐趣;
一旦我们做到前面这几步的话,那数学的学习自然就有乐趣,设想一下,我们面对一块黑板或者一张白纸,我们从导数的定义开始做起,一下就把这一套全都写下来了,不用看参考书,从导数的定义一直推出这个导数的运算法则,解出一些基本函数的导数,然后解出更复杂函数的导数。这里面能没有乐趣吗?当然有乐趣了。而且我们回答了心中的一个又一个的问题,而这些问题呢,它不但可以提高成绩,还可以跟其他人来交流,给其他人带来启发。
第九个台阶是能够投入,忘我的学习。
达到第八个台阶就很容易到达第九个台阶了,就是乐此不疲,我们称之为心流,flow。我们这样子学习三个小时的数学,感觉时间才过了半个小时一样。
四、五、六、这个台阶迈上去,那么我们数学考个优秀的成绩,考个120分,就不是问题了,如果我们到达了这七、八、九,这三个境界,那么考更高的成绩,像我刚才那个师弟讲的,考130分,140多分,那就是完全有可能的了,因为你都觉得数学学习都不是负担了,不是障碍了,不是痛苦而是享受了,解道难题会带来巨大的乐趣啊。
五、读不懂数学怎么办?
如果我们到了现在还觉得数学不太容易懂,高数书看起来很头疼,我们往下看看个例子。
我们看一下小平邦彦的故事,小平邦彦是亚洲第一获得菲尔兹奖的数学家,小平邦彦经常说自己天资不好,但是他从中学开始,就是那种做事情一丝不苟,全身心投入的人。他回忆自己第一次学习范德瓦尔登的《代数学》,几乎学不懂;然后就开始抄书,一直到抄懂为止。对于这样的一个大数学家,他在数学学习的初期,也遇到了巨大的困难,看书看不懂。所以我们经常说,看书看得很吃力,很费劲,这实际上本质上根本就不是个问题。那这个故事给你什么启发呢?
有人说“勤能补拙”,没错,我也是这么想的;还有的说“贵在坚持”,也没错,这也是这个故事所传达出的一个重要信息贵在坚持;有的也可能是说“不懂就要抄书”,至少抄书是个方法。还有人说“理解为王”,这也是这个故事讲的一个非常重要的一点,从几乎学不懂,然后最后到懂为止。
就理解很重要,我们对一个我们不理解的东西,怎么能心生乐趣呢?学问的乐趣就在于解惑,不断的解惑,这个解惑过程中产生的乐趣,如果我们一直不懂它,自己都认为不懂,那这个乐趣很难产生啊。
那么往下,跟大家分享一下,我对这个故事的启发
这故事不断在给我新的启发。
首先抄书能抄出数学家吗?如果抄书能抄出数学家的话,那满大街都是数学家了。他肯定是带着问题抄书,边抄边解答,直到懂为止,有了足够多的解答,就自然就懂了。他心里面的困惑都一一找到了答案,有一些是书上提示的答案,有一些是他根据书上的提示自己独立推导出来的答案,想出来的答案,那么就自然懂。
第二是,我们学习数学,必定需要扎实的基本功,这个基本功是什么?就是刚才讲的那个基本的思维技能,但可惜的是许多人不曾掌握这个思维技能,甚至都没有意识到,我们在做数学的过程中,在不断进行同样的思维操作,那个思维操作就是:基本的问答,不断在做问答,不断地在做加、减、乘、除法,不断地在从问题到定义,到定义的性质,到运算法则,到定理,到定理的应用去解题目,不断地在进行这样的或大或小的思维操作,这些思维操作,就是数学思维的基本的技能,也就是我们学数学的基本功。
第三点是,任何技能的学习,任何技能的掌握,必定是先慢后快,我们想这个,小平邦彦去抄书,如果他一本本地去抄,当但数学的文献浩如烟海,经典著作多得不得了,他如果都是这么慢慢的抄的话,那得抄到何年何月?正因为他抄的过程中,他不断地去熟悉和训练自己的思维技能,任何数学分支都有同样的结构,一旦熟悉这个技能,那就熟能生巧了。
反之,一旦我们前面的东西没掌握,认为它很简单,认为它很显然,认为它不值得一做,很可能在遇到那个考研题目的时候,我们都没有解题思路,甚至了解题思路,我们做不对,做不出来,
还有这么几个启发。
第一,不要纠结于有没有天资,除非努力过。即便是小平邦彦,他学数学的初期,仍然遇到很大的困难,我们在学高数的过程中,遇到困难的时候,看不懂的时候,题目做不出来的时候,经常会自我怀疑,是不是我数学真的就不行啊?我没有数学思维啊?
不是,不是那样子的。认知神经科学的研究表明,我们天生下来就有数学思维。严格的论证,之后跟大家来分享一下。不要再纠结这个问题了,除非我们努力过。连这样的数学家都做过这样的努力,那我们,我们问问自己,我们有没有做过这个与之相,相当的这个努力。
第二,“如果世界上有奇迹,那只不过是努力的代名词”,我们能解一道题目,中等难度的题目,只不过是由那些基本的知识点,那些基本的思维操作所导出来的。一道更难的题目也是一样的,我们解了一道很难的题目,会感到骄傲,感到是个奇迹,那只不过是我们以前以往点点滴滴的努力累积出来的,就是像积分一样,一点一点的积累出来的。
第三,没有绝对懂与不懂,关键是我今天有没有懂得更多。我今天懂了多少,我今天究竟懂了什么?我今天找到了哪些问题的答案,这是关键。包括我们在做一道题目的时候,我做错了,做错的话,我有什么收获?我做对了,也要问自己究竟收获了多少?一是一,二是二,三是三,我们有没有这么去做?这样做非常关键。