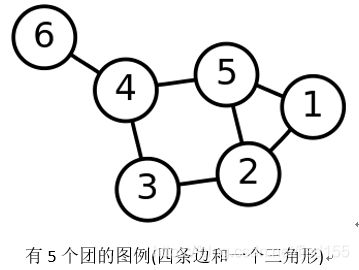
最大独立集和最大完全子图
定义
最大独立集：当且仅当对于U 中任意点u 和v所构成的边(u , v) 不是G 的一条边时，U 定义了一个空子图。当且仅当一个子集不被包含在一个更大的点集中时，该点集是图G 的一个独立集（independent set ），同时它也定义了图G 的空子图。最大独立集是具有最大尺寸的独立集（摘自：百度百科：最大独立集）。
最大完全子图：图中任意两顶点都直接相连的图，称为完全图，也称全连接图。图G的子图若为完全图，则称为图G的完全子图。最大的完全子图为最大完全子图。最大完全子图又称最大团，也称最大完备子图。
容易知道（画个图想想便知），一个图的最大独立集，等价于其补图的最大完全子图。
对应的，也有极大独立集、极大完全子图的概念。求解最大完全子图和极大完全子图，是经典的NP完全问题，目前只能使用回溯策略求解。但单纯的回溯效率很低，Bron-Kerbosch算法于1973年被提出，大大加快了搜索效率，之后又有各种优化。本文将对此进行简单介绍。
朴素的 Bron-Kerbosch算法
伪代码：
BronKerbosch1(R,P,X):
if P and X are both empty:
report R as a maximal clique
for each vertex v in P:
BronKerbosch1(R ⋃ {v}, P ⋂ N(v), X ⋂ N(v))
P := P \ {v}
X := X ⋃ {v}解释（摘自：百度文库：Bron_Kerbosch算法）：
在该算法中有四个集合：
。其中：
：目前已经在团中的结点的集合(temporary result)
：可能在团中的结点的集合(possible candidates)
：不被考虑的结点的集合(excluded set，在朴素的Bron Kerbosch算法表现为：包含该结点的最大团已经被搜索)
：结点 的所有直接邻居(有边直接相连)结点的集合。其中，
。
该算法文字描述为：从
找包含
也恢复到原来的状态，同时，将本次选择的结点从
Pivot 优化的 Bron-Kerbosch算法
朴素的Bron Kerbosch算法在有很多非最大团的情况下，效率不是很好。因为，该算法会遍历所有的团。该算法的其中一个变种是加入轴(pivot)，基本思想是选择一个结点
轴，最大团要么包含
伪代码：
BronKerbosch2(R,P,X):
if P and X are both empty:
report R as a maximal clique
choose a pivot vertex u in P ⋃ X
for each vertex v in P \ N(u):
BronKerbosch2(R ⋃ {v}, P ⋂ N(v), X ⋂ N(v))
P := P \ {v}
X := X ⋃ {v}前述示例的执行步骤：
退化序优化的 Bron-Kerbosch算法
预备知识
Induced subgraph
在介绍 induced subgraph（诱导子图）前，先回顾下 spanning subgraph（生成子图）。
生成子图：对于图 
, 若 
满足 
，则
为 
的生成子图。简单来说，生成子图的顶点与原图的顶点一样，但边是原图边的子集。
诱导子图：对于图 , 若 满足 
，并且 
当且仅当 
，则 为 的诱导子图。也就是说，顶点可以少，一旦选定了顶点，则顶点对应的所有的边都要选进来。
Degeneracy
本部分翻译自 Wiki: Degeneracy
Degeneracy（退化）：如果图的结点存在一种序列，使得每个结点和它所有前驱形成的诱导子图中，该结点度不超过K，则称该图为 k-degenerate graph（K-退化图）；可以找到最小的K值，使得原图满足K-退化图，此时对应的序列即为退化序（degeneracy ordering）。K-退化图又称 K-诱导图。容易知道，树结构为 1-诱导图。
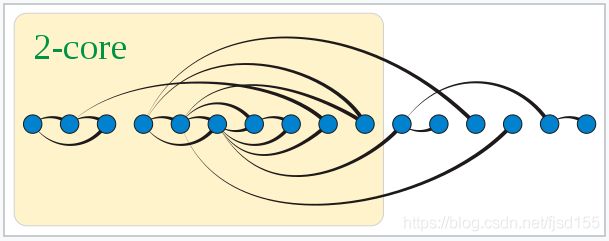
K-退化图的K值，与 K-core number（K核值）是相等的，也与 coloring number（染色数）可能一致。这里大致说一说 K-core。K-core是原图的子图，该子图满足条件：任意一个顶点的度数都不小于 K。上述图中，展示的便是一个 2-degenerate graph，以及对应的 2-core（黄色部分）。怎么理解呢？反复删除度数小于2的点，最终保留下来的便是 2-core。其实这一反复删除的操作过程便是求解 K-degenerate graph和 K-core 的逆向过程（下文将详细介绍）。K-core在很多领域（如：社交网络、生物信息学等）中都有用到（可参考相关资料详细了解其应用价值）。
求解算法：
初始化结果序列 L。
定义d(v)为：顶点v所有不在 L中的邻接顶点个数。初始化的 d(v)即使v的度数。
定义D(i)为：所有度数为 i 的顶点集合。初始化D(i)。
初始化k=0。
重复下列计算：
依次扫描D(0), D(1), ...直至D(i)不为空。
令k=max(k,i)。
从D(i)中拿出一个顶点v，将v加入到 L的最前面，并将D(i)中删除v。
更新d数组和D数组，即：对于v的所有邻居u，对应的d(u)值都减1；D数组根据d值更新。
最终得到的K即是最小的K值，L序列即是可行的退化序列，K-core 就是第一次对D(K)取顶点前尚未进入L的顶点构成的子图（其实求解过程可以得出各个 i-core [ i=2,3,...K ] ）。
使用退化序优化的思路
如果算法在从
伪代码：
BronKerbosch3(G):
P = V(G)
R = X = empty
for each vertex v in a degeneracy ordering of G:
BronKerbosch2(R ⋃ {v}, P ⋂ N(v), X ⋂ N(v))
P := P \ {v}
X := X ⋃ {v}前述示例的执行步骤：
在Pivot 优化和退化序优化后，Bron-Kerbosch算法的求解效率得到极大的提升。
C++代码实现（代码借鉴自：无向图的极大团、最大团(Bron-Kerbosch算法)，笔者加入了degeneracy ordering优化代码）：
#include
#include
#include
#include
#include
#define MAX_N 1500
using namespace std;
bool mp[MAX_N][MAX_N];
int some[MAX_N][MAX_N], none[MAX_N][MAX_N], all[MAX_N][MAX_N];
int n, m, ans;
int L[MAX_N], degeneracyOrdering[MAX_N];
int degree[MAX_N], DegreeVertex[MAX_N][MAX_N], numberVertex[MAX_N];
int k, L_number;
ifstream input;
ofstream output;
int kk;
stringstream ss;
/* d: the depth;
an: the number of all_set;
sn: the number of some_set;
nn: the number of none_set.
*/
void dfs(int d, int an, int sn, int nn) {
/*
cout<<"DFS: { ";
for (int i = 0; i < an; i++) cout<=kk) {
ans++;
for (int i = 0; i < an-1; i++) output<k) k = i;
int v = DegreeVertex[i][0];
L[L_number++] = v;
degree[v] = -1;
for (int u = 1; u <= n; u++)
if (mp[u][v]==1) degree[u]--;
memset(numberVertex, 0, sizeof numberVertex);
memset(DegreeVertex, 0, sizeof DegreeVertex);
for (int v = 1; v <= n; v++)
if (degree[v]>=0)
DegreeVertex[degree[v]][numberVertex[degree[v]]++] = v;
}
memset(degeneracyOrdering, 0, sizeof degeneracyOrdering);
for (int i = 0; i < n; i++)
degeneracyOrdering[i] = L[n-i-1];
cout<<"The degeneracy ordering is: ";
for (int i = 0; i < n; i++)
cout<>kk;
if (!input) {
cout<<"open error!"<>n>>m;
memset(mp, 0, sizeof mp);
memset(degree, 0, sizeof degree);
for(int i = 0; i < m; i++) {
int u, v;
input>>u>>v;
mp[u][v] = mp[v][u] = 1;
degree[v]++;
degree[u]++;
}
int tmp = work();
cout<<"The number of set is: "<
对于最大完全子图（最大独立集）问题（仅仅求最大），还可以进一步剪枝优化（如，预估后续搜索能否超过当前最大值），本文暂不讨论，可参考相关资料（如：最大独立集求解、最大团等）
对于二分图的最大独立集问题，有更好的解法，感兴趣的可搜索相关资料。
参考资料：
百度文库：Bron_Kerbosch算法
Bron–Kerbosch算法-最大独立集与最大团
无向图的极大团、最大团(Bron-Kerbosch算法)