括号生成(结合Catalan数详细分析)
题目
给出n代表生成括号的对数,请你写出一个函数,使其能够生成所有可能的并且有效的括号组合。
例如,给出n = 3,生成结果为:
[
"((()))",
"(()())",
"(())()",
"()(())",
"()()()"
]
PS:本题源自[leetcode 22]
理论基础(Catalan数,卡特兰数)
Catalan数列是序列
C 0 , C 1 , C 2 , … C n , … C_0, C_1,C_2,\ldots C_n,\ldots C0,C1,C2,…Cn,…
其中
C n = 1 n + 1 ( 2 n n ) (*) C_n=\frac 1 {n+1}\binom{2n}{n}\tag{*} Cn=n+11(n2n)(*)
有递推式
C n = C 0 C n − 1 + C 1 C n − 2 + ⋯ + C n − 1 C 0 , n ≥ 1 (**) C_n=C_0C_{n-1}+C_1C_{n-2}+\cdots+C_{n-1}C_0,\quad n\ge 1\tag{**} Cn=C0Cn−1+C1Cn−2+⋯+Cn−1C0,n≥1(**)
说明:
- 递推式 ( ∗ ∗ ) (**) (∗∗)可以通过母函数法(生成函数)算出 C n C_n Cn的表达式即 ( ∗ ) (*) (∗)式。
- 只要某一序列满足 ( ∗ ) , ( ∗ ∗ ) (*),(**) (∗),(∗∗)中的一个,则可以称该序列为Catalan数列。
为了引出本题的解题思路来源和证明算法的正确性,下面以两个最经典的使用Catalan数的组合模型为例(这里仅做概述,提取解题的关键内容,详细的请查阅资料如机工出版社的《组合数学》)
-
问题一:用凸 n + 1 n+1 n+1 边形的
不相交的对角线将其划分成三角形区域的方法数 h n h_{n} hn(为了方便后面书写,这里取 h n + 1 = C n h_{n+1}=C_n hn+1=Cn,仍然是Catalan数列的一部分,仍可称作Catalan数)(先规定初始值,由Catalan数定义式 ( ∗ ) (*) (∗)可算出 h 1 = C 0 = 1 h_1=C_0=1 h1=C0=1,为了解释“划分2边形”的方法数,几何上我们将
一条边定义为没有内部区域的“单、双边形”)
一般情况如 n + 1 = 3 n+1=3 n+1=3时,凸三边形也就是我们熟知的三角形,不需做任何划分就已经是三角形区域(不划分也是一种划分方案),所以 h 2 = 1 h_2=1 h2=1,
又如 n + 1 = 5 n+1=5 n+1=5时,有如下划分方法,所以 h 4 = 5 h_4=5 h4=5,

定理 h n ( n ≥ 2 , h 1 = 1 ) h_n(n\ge2, h_1=1) hn(n≥2,h1=1)有如下递推式
h n = h 1 h n − 1 + h 2 h n − 2 + ⋯ + h n − 2 h 2 + h n − 1 h 1 = ∑ k = 1 n − 1 h k h n − k , n ≥ 2 (1.1) h_{n}=h_1h_{n-1}+h_2h_{n-2}+\cdots + h_{n-2}h_2+h_{n-1}h_1=\sum_{k=1}^{n-1}h_kh_{n-k},\quad n \ge 2\tag{1.1} hn=h1hn−1+h2hn−2+⋯+hn−2h2+hn−1h1=k=1∑n−1hkhn−k,n≥2(1.1)证明 显然 n = 2 n=2 n=2是我们上面举的三角形的例子,并且通过枚举可知 h 2 = 1 h_2=1 h2=1,可以验证这时递推式(1.1)成立( 1 = h 2 = ∑ k = 1 1 = h 1 h 1 = 1 1=h_2=\sum_{k=1}^{1}=h_1h_1=1 1=h2=∑k=11=h1h1=1)。
直接考虑 n + 1 ≥ 4 n+1\ge 4 n+1≥4时,划分凸 n + 1 n+1 n+1 边形 K K K
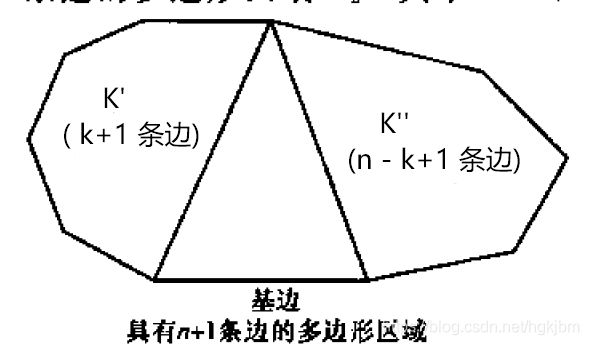
我们固定 K K K的一条边并把它叫做基边,在 K K K的每个划分中,这条基边一定是某一三角形区域的一边,而它所在的三角形一定将多边形 K K K划分成如上图的两个多边形,凸 k + 1 k+1 k+1 边形 K ′ K' K′和凸 n − k + 1 n-k+1 n−k+1 边形 K ′ ′ ( k ≥ 1 ) K''(k\ge1) K′′(k≥1)。
我们反过来看,选择含这一基边的三角形区域,将 K K K划分成两个多边形 K ′ , K ′ ′ K',K'' K′,K′′,而划分多边形 K ′ , K ′ ′ K',K'' K′,K′′的方案数分别为 h k , h n − k h_{k},h_{n-k} hk,hn−k,由乘法原理知此时方案数为 h k h n − k h_{k}h_{n-k} hkhn−k,特定地选择三角形区域让 k : 1 → n − 1 k:1\rightarrow n-1 k:1→n−1,所以总划分方案 h n = ∑ k = 1 n − 1 h k h n − k h_n=\sum_{k=1}^{n-1}h_kh_{n-k} hn=∑k=1n−1hkhn−k,得证!综上, h n h_n hn满足递推式 ( ∗ ∗ ) (**) (∗∗),这种划分方案数 h n h_n hn为Catalan数。
-
问题二:满足任意前 k ( ≤ 2 n ) k(\le 2n) k(≤2n)项和非负的由 + 1 , − 1 +1,-1 +1,−1构成的长 2 n 2n 2n序列的个数为 C n C_n Cn
由 + 1 , − 1 +1,-1 +1,−1构成的长 2 n 2n 2n序列
a 1 , a 2 , ⋯ , a 2 n − 1 , a 2 n a_1,a_2,\cdots,a_{2n-1},a_{2n} a1,a2,⋯,a2n−1,a2n满足
∀ 1 ≤ k ≤ 2 n , a 1 + ⋯ + a k ≥ 0 (2.1) \forall 1\le k\le 2n,\quad a_1+\cdots+a_k\ge 0 \tag{2.1} ∀1≤k≤2n,a1+⋯+ak≥0(2.1)我们将其定义为
可满足的序列 { a n } \{a_n\} {an};反之定义不可满足的序列 { b n } \{b_n\} {bn},当
∃ 1 ≤ k ≤ 2 n , b 1 + ⋯ + b k < 0 (2.2) \exists 1\le k\le 2n,\quad b_1+\cdots+b_k< 0 \tag{2.2} ∃1≤k≤2n,b1+⋯+bk<0(2.2)现在对于所有由 + 1 , − 1 +1,-1 +1,−1构成的长 2 n 2n 2n序列中,记可满足的序列有 A n A_n An个,不满足的序列有 B n B_n Bn个,显然(不是可满足的就是不可满足的),于是有 A n + B n = ( 2 n n ) = ( 2 n ) ! n ! n ! (2.3) A_n+B_n=\binom{2n}{n}=\frac{(2n)!}{n!n!} \tag{2.3} An+Bn=(n2n)=n!n!(2n)!(2.3)
我们所需求的 A n A_n An无法直接求出,于是希望通过求出 B n B_n Bn来间接得出。
不可满足的序列 { b n } \{b_n\} {bn}其实也不好直接计数,但若注意到一下一一对应关系,那么计数将变得十分简单:
对于满足(2.2)的不可满足的序列 { b n } \{b_n\} {bn},我们找到第一个这样的 k k k,观察发现必有
-
b 1 + b 2 + ⋯ + b k − 1 = 0 b_1+b_2+\cdots+b_{k-1}=0 b1+b2+⋯+bk−1=0
-
b k = − 1 b_k=-1 bk=−1, k k k为奇数
将前 k k k个数的正负号翻转,其余保持不变。由于前 k − 1 k-1 k−1个数中 + 1 , − 1 +1,-1 +1,−1个数相等,翻转后对 ± 1 \pm1 ±1总数没影响,所以对整个序列 { b n } \{b_n\} {bn}而言,翻转后有 n + 1 n+1 n+1个1, n − 1 n-1 n−1个 − 1 -1 −1。反过来看,含有 n + 1 n+1 n+1个1, n − 1 n-1 n−1个 − 1 -1 −1的长 2 n 2n 2n序列一定能找到某一个 k k k,作上面相同的翻转操作后能得到对应的不可满足的序列 { b n } \{b_n\} {bn},由可重排列的公式,含有 n + 1 n+1 n+1个1, n − 1 n-1 n−1个 − 1 -1 −1的序列有
( 2 n ) ! ( n + 1 ) ! ( n − 1 ) ! = B n \frac{(2n)!}{(n+1)!(n-1)!}=B_n (n+1)!(n−1)!(2n)!=Bn于是 A n = ( 2 n ) ! n ! n ! − B n = 1 n + 1 ( 2 n n ) A_n=\frac{(2n)!}{n!n!}-B_n=\frac 1 {n+1}\binom{2n}{n} An=n!n!(2n)!−Bn=n+11(n2n)。
综上 A n = C n A_n=C_n An=Cn。
两种解题思路
用类似上面的方法可以证明这样的有效串个数恰为Catalan数。
同样的,官方给出了两种解法——闭合数和回溯法,这两种方法也对应上面对Catalan数的两种不同理解
- 闭合数

像选择基边一样,我们固定一对括号(如图中红色括号对,这里考虑到有效括号对串首一定是开括号,且一定可以找到与之对应的闭括号) ,可以将这 n n n对有效串分成 L L L和 R R R两部分,共有 h k h n − 1 − k h_kh_{n-1-k} hkhn−1−k个生成方式,得到的递推与递推式 ( ∗ ∗ ) (**) (∗∗)一致。说明这样的有效串个数恰为Catalan数,与事实符合,算法的正确性自动得到证明!
对编程而言,只需对 L , R L,R L,R部分递归地调用生成相应对数的函数即可
//以Java实现为例,摘自官方解答
class Solution {
public List<String> generateParenthesis(int n) {
List<String> ans = new ArrayList();
if (n == 0) {
ans.add("");
} else {
for (int c = 0; c < n; ++c)
for (String left: generateParenthesis(c))
for (String right: generateParenthesis(n-1-c))
ans.add("(" + left + ")" + right);
}
return ans;
}
}
![]()
说明:
- 由于该算法重复调用参数较小的实例,使得这一解答在时间上的可优化空间很大
- 例如添加一个 m e m o memo memo数组保存算过的 k k k对有效括号串的结果(动态规划)
(更新添加 m e m o memo memo数组后的通过时间)
![]()
这种自顶向下(递归式)的动态规划如果不用 m e m o memo memo保存计算过的子问题,其 反复的堆栈操作 相比 用于保留子问题结果所消耗的空间 更大,可谓得不偿失!
//动态规划处理(自顶向下)
class Solution {
List<String> [] memo;
public List<String> generateParenthesis(int n) {
memo = new List[n+1];
return dp(n);
}
public List<String> dp(int n){
if(memo[n] != null) return memo[n];
memo[n] = new ArrayList();
if(n == 0) memo[n].add("");
else{
for (int c = 0; c < n; ++c)
for (String left: dp(c))
for (String right: dp(n-1-c))
memo[n].add("(" + left + ")" + right);
}
return memo[n];
}
}
-
回溯法
我们发现将 ‘ ( ’ ‘(’ ‘(’ → + 1 \rightarrow+1 →+1, ‘ ) ’ → − 1 ‘)’\rightarrow-1 ‘)’→−1,则和第二个例子完全一致,括号匹配由式(2.1)确保

现在考虑回溯算法的写法
-
出口:生成串长已达到 2 n 2n 2n,将该串加入答案数组,退出算法
-
本层递归可以添加
'('或')'但需要在满足下面条件的情况下进入下一层递归:- o p e n < n open < n open<n( o p e n open open指开括号
'('的个数, c l o s e close close指闭括号)的个数)
可以添加(, o p e n + 1 open+1 open+1然后进入下轮层递归 - c l o s e < o p e n close < open close<open
可以添加), c l o s e + 1 close+1 close+1然后进入下轮层递归
说明:
- o p e n < n open < n open<n( o p e n open open指开括号
-
条件2确保从递归开始就满足(2.1)式 -
而对于满足
条件2的序列,可以随意添加'('(添加 + 1 +1 +1),因为添加 + 1 +1 +1不会破坏(2.1)式的性质 -
条件1仅用来确保有效对数不超过 n n n -
由
条件1和条件2确保不遗漏的生成“满足任意前 k ( ≤ 2 n ) k(\le 2n) k(≤2n)项和非负的”由 + 1 , − 1 +1,-1 +1,−1构成的长 2 n 2n 2n序列,所以有效括号串数自然不会遗漏,算法正确性自动得到保证
class Solution {
public List<String> generateParenthesis(int n) {
List<String> ans = new ArrayList();
backtrack(ans, "", 0, 0, n);
return ans;
}
public void backtrack(List<String> ans, String cur, int open, int close, int max){
if (cur.length() == max * 2) {
ans.add(cur);
return;
}
if (open < max)
backtrack(ans, cur+"(", open+1, close, max);
if (close < open)
backtrack(ans, cur+")", open, close+1, max);
}
}
![]()
算法复杂度分析
由于篇幅问题,算法复杂度的分析请看下一篇时间复杂度篇