现代控制理论6——能控、能观及其对偶原理、线性变换、结构分解

注：本文是在MOOC平台上学习西北工业大学《现代控制理论基础》（郭建国、赵斌、郭宗易）的课程进行随笔记录与整理

一.凯莱-哈密尔顿定理

任何一个n阶矩阵，其n到0次幂都是线性相关的，其线性相关的参数和该矩阵的特征多项式参数相同。

推论1：

任何一个n阶矩阵的n及其以上幂次，均可以用n-1次幂直到0次幂的线性结合。

推论2：

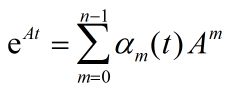
任何一个n阶矩阵的矩阵指数阵，均可以用n-1次幂直到0次幂的线性结合。

二.线性定常连续系统的能控性

1.能控性定义

分为状态能控性和输出能控性：
状态能控性：只与状态方程有关，描述输入信号与状态变量的关系；
输出能控性：与状态方程、输出方程均有关系，描述输入信号对输出的影响。
主要讨论的是状态能控性。

能控性定义：
设连续系统状态方程为：x`=Ax+Bu
在有限时间间隔t0 ≦ t ≦ tf 内，存在无约束的分段容许连续控制函数 u(t) ，能使系统从任意初态 x(t0) 转移到终态 x(tf)=0，则称系统是状态完全能控的，简称能控的

即：把系统状态从任意一点转移到稳定点（对于线性系统即原点）
为了便于理解举出两例：

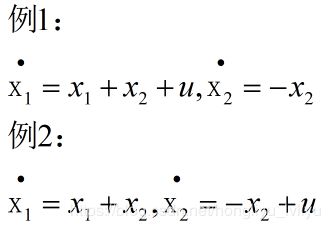
在1中，x2的导只有x2决定，与输入u无关，因此不完全可控即不可控；在2中，x1的导虽然不直接又u决定，但会通过x2影响x1，此时是完全能控即能控的。

2.能控性判据

秩判据：
rank[B AB …A^(n-1)B] = rank Qc = n
n为矩阵A的维数

(为什么上面要写凯莱哈密尔顿定理呢，因为能控判据的证明会用到。。但是写证明过程麻烦且用处不大。。所以就省略了（狗头）)

注意：
状态能控性只与状态方程中的A,B矩阵有关，若系统能控，则==[A,B]为能控对==。
（wo在看到一些论文的时候感觉看到“能控对”的说法还挺多，在校学的时候对这个说法都没有印象。。所以应该还挺常用的？）

对于离散系统的能控判据，和连续系统类似，只是状态方程有变化，连续中的A相当于离散中的Ф， 连续中的B相当于离散中的G

三.线性定常连续系统的能观测性

1.能观测性定义

能观：由系统的输出估计状态的可能性
能观定义：
系统状态方程为：x`=Ax+Bu, y=Cx+Du
已知输入u(t),通过在有限时间间隔t0 ≦ t ≦ tf 内测量到的输入y(t)，能唯一确定任意初始状态x(t0)的每一分量，则称系统是完全能观测的。

2.能观测性判据

秩判据：

注意：
状态能观测性只与状态方程中的A,C矩阵有关，若系统能观测，则==[A,C]对 称为 能观测对==。

离散的能观与能控一样，可以通过线性定常连续系统进行类比。

四.对偶原理

能控与能观的矩阵存在对偶关系：

这种对偶关系反应了控制问题与估计问题的对偶性。

对偶原理：
如果原系统S1能控（能观），则对偶系统S2是能观（能控）的。
或者：原系统S1能控（能观）的条件，和对偶系统S2能观（能控）的条件完全相同。

呈现在框图上，即输入输出进行了互换（图上方向相反）
S1:
S2:
应用：可以将一个系统的能控（能观）转换成另一个系统的能观（能控）问题来处理。

五.线性变换后的特性

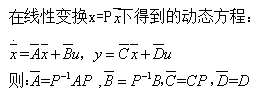
在如图的线性变换下，系统的性质有什么改变呢？
外部特性：
1）系统传递矩阵（G）不变——输入输出特性不变
内部特性：
2）系统特征多项式、特征值不变——稳定性不变
3）变换后能控矩阵秩相同——系统能控性不变
4）变换后能观矩阵秩相同——系统能观测性不变
综上，系统线性变换不会改变内部/外部特性，也不会改变内在/外在性质。

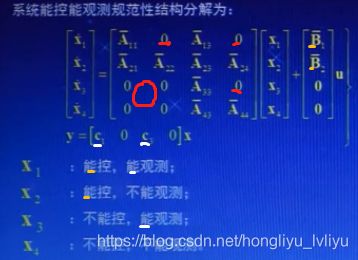
六.线性定常系统的规范形结构分解

结构分解的意义：
系统中有一个状态变量不能控，则系统不能控；
系统中有一个状态变量不能观，则系统不能观；
不能控系统可能含有能控、不能控两种状态变量；
不能观系统可能含有能观、不能观两种状态变量；

根据系统的能控/不能控，能观/不能观，可以分成四类子系统：能控能观，能控不能观，不能控能观，不能控不能观
传递函数的极点只反映 能控能观 部分的特征值，但其他部分虽然不出现在传函中，但必然会影响系统的稳定性和品质。

可以通过以下的变换方法，对系统进行线性变换，将能控/能观 与 不能控/不能观 的部分分开。
★系统不能控时：
在能控矩阵Qc中选出r个线性无关列向量，另外附上任选的（n-r）个列向量，构成非奇异的变换矩阵。

在方框图中可以看出下面的部分是不受输入u影响的：

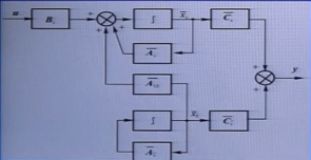
★系统不能观测时：
在能观测矩阵Qo中选出l个线性无关列向量，另外附上任选的（n-l）个列向量，构成非奇异的变换矩阵。

在方框图中可以看出下面的部分是不影响输出y的：

如下为能控能观分解的典型结构：
能控问题：A的左下角为0块矩阵；输入矩阵中有0
能观测问题：A分块矩阵的右上角为0；输出矩阵中有0