KeeLoq算法深入剖析
KeeLoq算法深入剖析
请支持原创,尊重原创,转载请注明出处:http://blog.csdn.net/kangweijian(来自kangweijian的csdn博客)
1 KeeLoq算法介绍
1.1 KeeLoq运算规则
KeeLoq算法的核心思想就是用8byte密钥加密4byte明文,从而得到4byte密文或者用8byte密钥解密4byte密文,还原出原4byte明文。KeeLoq算法演算过程需要定义一个数据寄存器,用于存放4byte明文y31~0或者4byte密文y31~0,和一个密钥寄存器,用于存放8byte密钥k63~0。
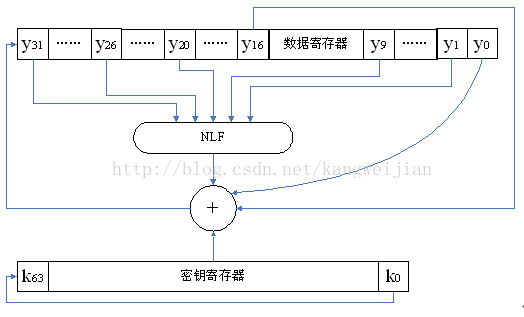
KeeLoq数据加密过程模型图如图1所示,首先定义一个非线性表,这个非线性表有5bits输入码,1bit输出码。它在数据寄存器中间隔均匀地取5bits: y31、y26、y20、y9、y1,通过NLF(Nonlinear Logic Function)运算产生一个输出码。输出码再与数据寄存器中的y16与y0以及密钥寄存器中的k0进行异或运算后生成1bit加密数据码。每生成1bit加密数据码,密钥寄存器和数据寄存器分别进行移位,密钥寄存器作循环移位,加密数据码作为数据寄存器移位的输入,重复上述步骤528次后,得到4byte的输出密文。
NLF(x4,x3,x2,x1,x0)=x4x3x2^x4x3x1^x4x2x0^x4x1x0^x4x2^x4x0^x3x2^x3x0^x2x1^x1x0^x1^x0
图1 KeeLoq加密模型图
KeeLoq数据解密模型图如图2所示,其过程的运算方法与数据加密过程的运算方法基本一致,只是其中运算数据数据位发生变化。非线性表的5bits输入码改成从数据寄存器中间隔均匀地取固定5bits:y30、y25、y19、y8、y0。产生1bit输出码后输出码再与数据寄存器中的y31与y15以及密钥寄存器中的k15进行异或运算后生成1bit解密数据码。每输出1bit解密数据码后,密钥寄存器和数据寄存器分别进行移位,密钥寄存器作循环移位,解密数据码作为数据寄存器移位的输入,重复上述步骤528次后,还原出4byte的明文。
图2 KeeLoq解密模型图
1.2 KeeLoq实现机制
采用KeeLoq方法实现数据编码和解码,其通信过程需严格按照下述过程进行。首先,要求编码端和解码端都需要有非易失性存储空间以存储8byte密钥(用于编解码,可编程且不被发送不可泄露)、3byte序列号(用于区分不同的编码端)、2byte同步计数值(用于产生编码滚动效果,每完成一次数据传送后,其值自加1后更新)、1byte识别码(序列号的低1byte)和4byte种子码(安全模式下用来生成密钥)。
当用户有按键操作时,KeeLoq编码端将1byte功能键、1byte识别码、2byte同步计数值组合成4byte明文,按照图1的NLF运算规则加密成4byte密文,再加上4byte固定码(3byte序列号、1byte功能键),组合成一组8byte的编码数据发送。由于每次发送过程,同步计数值自加1,使得每次发送的4byte密文都是惟一的、不规则的、且不重复,故称之为滚动码,可以有效的防止密码捕捉和密码拷贝。由于8byte的编码组合达到2^64=1.84*10^19,因而可以有效的防止密码扫描。
解码端接收到8byte密文数据后,首先匹配编码端和解码段的3byte序列号一致后,按照图2的KeeLoq解码运算规则还原出4byte明文。再校验明文中的识别码以及功能键正确后,最后判断同步计数值是否合理增加。确认成功后根据功能键定义,控制相应执行机构动作。
2 KeeLoq算法不足与改进
2.1 KeeLoq算法的安全性与不足
KeeLoq算法的NLF运算规则,使得一个很小的输入变化量,也会造成很大的输出变化量,产生的编码滚动效果。密码分析者就无法通过输入微小的变化来观察分析输出的变化,从而破解出密钥,使得KeeLoq算法具有安全性高特点。
虽然KeeLoq算法发布于20世纪80年代,但直到2007年,Bogdanov才首次对KeeLoq算法进行攻击,他使用猜测-决定和滑动技术来完成攻击,攻击的时间复杂度为252,空间复杂度为16GB。在2008年,Courtois等人提出了4种滑动-代数攻击方法,其主要思想是利用KeeLoq算法连续64圈圈函数形成的置换和圈结构与随机置换圈结构的差异,先攻击密钥的前16bits,再攻击剩余的48bits。折合计算复杂性至少约为O(2^43)次加密。2010年,游建雄等人提出3 种不同采用面向字节的差分故障攻击方法,其中攻击效率最好的方法,恢复1 bit 密钥信息平均只需要0. 707617 个错误,恢复8byte的密钥只需要46个错误。
虽然KeeLoq算法发布后至今已经取得很多有效的攻击,大大降低了计算时间复杂度,但是也增加了计算空间复杂度,并且需要一定数量的已知前提。导致在实际密码破解过程中难度系数高,故其安全性足以保证,在实际应用当中有着广泛应用。
2.2 KeeLoq算法的改进
KeeLoq加密算法是4byte的分组密码,密钥长度较短,仅为8byte。算法发布至今已有相关文献报导取得有效攻击,针对这一现状及上述算法不足之处,为了进一步提高 KeeLoq算法安全性,本文分别对编解码过程及密钥管理进行改进。
2.2.1 编解码过程的改进
首先,编解码过程借鉴了三重数据加密算法(3DES,Triple Data Encryption Algorithm),提出三重KeeLoq算法。即采用三个不同密钥分别对明文、第一次获得密文及第二次获得密文进行KeeLoq加密后,生成最终密文。解密过程则是,先用第三个密钥对最终密文解密得到第二次密文,用第二个密钥对第二次密文解密得到第一次密文,最后用第一个密钥对第一次密文解密得到原始明文。该过程是KeeLoq算法的一种更安全的变形,通过增加KeeLoq的密钥长度来提高针对KeeLoq攻击的时间复杂度和计算复杂度,以进一步提高其安全性。
2.2.2 KeeLoq密钥管理机制的改进
以Microchip的KeeLoq密钥管理机制为例。Microchip定义了一套学习模式来管理密钥。学习模式目的是为了编码端与解码端进行配对。在学习过程中,首先按下学习按键之后,解码端解码密文后,校验功能键和识别码正确后,就将该编码端的同步计数值和序列号存到自身的非易失性存储空间,这样就表示学习成功。学习成功之后,编码端才能与解码端正常通信。
Microchip总共提出了三种学习模式(密钥管理机制)。第一种:简易学习模式。简易学习模式无法修改密钥,一旦密钥泄露,后果无法挽回。
第二种:标准学习模式。标准学习模式在学习过程中可同时按下全部或多个功能按钮,则该模式将原始密钥和编码端的序列号通过某种算法生成新的密钥,解码端接收到密文后,通过原始密钥解密不正确之后,就会尝试用原始密钥+序列号生成新的密钥来解密密文,一旦解密成功,解码端就会在自身的非易失性存储空间内将密钥更改掉。很明显,标准学习模式的安全性就比简易学习模式高了许多,原始密钥和序列号同时泄漏的难度明显比单单仅原始密钥泄漏的难度高了多。
第三种:安全学习模式。安全学习模式比标准学习模式多了一个种子码,学习过程与标准模式差不多,差别仅在于标准模式生成新密钥的方式是:原始密钥+序列号。而安全学习模式是:原始密钥+种子码+序列号通过某种算法生成新的密钥。
三种学习模式,其安全性一层比一层高。简易学习模式的安全性完全依赖于密钥不丢失,标准学习模式的安全性依赖于密钥和序列号不同时丢失,安全学习模式的安全性依赖于密钥、种子码和序列号不同时丢失。当然了生成新密钥的算法也不能丢失。
说到这里,我们再说说密钥管理机制的改进,其实有很多种。比如我们可以有一个手动输入的种子码让其放于固定码中发送出去,这样就如我们QQ或者Google帐号被盗窃后,直接手动修改密码那般惬意。或者如果无法做到手动修改,我们可以做一个随机生成器,随机生成一个种子码,这样完全不必担心种子码在哪个环节会泄漏,因为我们自己都不知道种子码会是多少。总的来说,密钥管理机制的改进取决于KeeLoq算法的应用环境中,视具体情况而定。当然Microchip已经做的非常好了。但是凡事没有尽善尽美,哪怕我们可以做出一点点的进步。
附KeeLoq算法源码
源码一:KeeLoq.c (32位处理器)
#include
#include
using namespace std;
unsigned long long int SERX=0xefcdab2143658709;
unsigned long long int key=0xefcdab2143658709;
unsigned int HOPE;
unsigned int c=0;
int NLF[2][2][2][2][2];
int getBit(unsigned long long int source,int n) {
unsigned long long int temp0=((long long int) 1<>1)|0x80000000;
}else{
HOPE=(HOPE>>1)&0x7fffffff;
}
}
void RlcHOPE(){
if(c!=0){
HOPE=(HOPE<<1)|1;
}else{
HOPE=(HOPE<<1)&0xFFFFFFFE;
}
}
void CRYPT() {
//key=SERX;
for (int i = 0; i < 528; i++) {
int nlf=NLF[getBit(HOPE, 31)][getBit(HOPE, 26)][getBit(HOPE, 20)][getBit(HOPE, 9)][getBit(HOPE, 1)];
int y16=getBit(HOPE, 16);
int y0=getBit(HOPE, 0);
int k=getBit(key, i%64);
int result=nlf^y16^y0^k;
if (result!=0) {
c=1;
}else {
c=0;
}
RrcHOPE();
}
}
void DECRYPT() {
key=SERX;
for (int i = 528; i >0; i--) {
int nlf=NLF[getBit(HOPE, 30)][getBit(HOPE, 25)][getBit(HOPE, 19)][getBit(HOPE, 8)][getBit(HOPE, 0)];
int y15=getBit(HOPE, 15);
int y31=getBit(HOPE, 31);
int k=getBit(key, (i-1)%64);
int result=nlf^y15^y31^k;
if (result!=0) {
c=1;
}else {
c=0;
}
//printf("step %d : %x %x %x %x %x %x\n",i,HOPE,nlf,y15,y31,k,result);
RlcHOPE();
}
}
int main(){
NLF[0][0][0][0][0]=0;
NLF[0][0][0][0][1]=1;
NLF[0][0][0][1][0]=1;
NLF[0][0][0][1][1]=1;
NLF[0][0][1][0][0]=0;
NLF[0][0][1][0][1]=1;
NLF[0][0][1][1][0]=0;
NLF[0][0][1][1][1]=0;
NLF[0][1][0][0][0]=0;
NLF[0][1][0][0][1]=0;
NLF[0][1][0][1][0]=1;
NLF[0][1][0][1][1]=0;
NLF[0][1][1][0][0]=1;
NLF[0][1][1][0][1]=1;
NLF[0][1][1][1][0]=1;
NLF[0][1][1][1][1]=0;
NLF[1][0][0][0][0]=0;
NLF[1][0][0][0][1]=0;
NLF[1][0][0][1][0]=1;
NLF[1][0][0][1][1]=1;
NLF[1][0][1][0][0]=1;
NLF[1][0][1][0][1]=0;
NLF[1][0][1][1][0]=1;
NLF[1][0][1][1][1]=0;
NLF[1][1][0][0][0]=0;
NLF[1][1][0][0][1]=1;
NLF[1][1][0][1][0]=0;
NLF[1][1][0][1][1]=1;
NLF[1][1][1][0][0]=1;
NLF[1][1][1][0][1]=1;
NLF[1][1][1][1][0]=0;
NLF[1][1][1][1][1]=0;
while(1){
scanf("%x",&HOPE);
CRYPT();
printf("%x\n",HOPE);
DECRYPT();
printf("%x\n",HOPE);
}
return 0;
}
源码二:KeeLoq.h+KeeLoq.c(8位微机)
unsigned char SERX[]={0XEF,0XCD,0XAB,0X21,0X43,0X65,0X87,0X09};
unsigned char key[]={0X09,0X87,0X65,0X43,0X21,0XAB,0XCD,0XEF};
unsigned char NLF[2][2][2][2][2];
unsigned char getBit(unsigned char source[],int n);
unsigned char * RRC(unsigned char source[],char c,char n);
unsigned char * RLC(unsigned char source[],char c,char n);
unsigned char * CRYPT(unsigned char *source);
unsigned char * DECRYPT(unsigned char *source);
void init();#include
#include"KeeLoq.h"
/*****************************
*
* @param source
* @param n
* @return source的第n个位数
*
******************************/
unsigned char getBit(unsigned char source[],int n)
{
unsigned char temp0=(unsigned char)1<<(n%8);
unsigned char temp1=source[n/8]&temp0;
if(temp1!=0)
{
return 1;
}
return 0;
}
/***********************
*
* @param source[]
* @param c 进位标志位
* @param n 数组长度
* @return source数组带进位右移
*
***********************/
unsigned char * RRC(unsigned char source[],char c,char n)
{
int i=0;
unsigned char temp;
for(i=n-1;i>=0;i--)
{
temp=source[i];
if(c!=0){
source[i]=(source[i]>>1)|0x80;
}else{
source[i]=(source[i]>>1)&0x7f;
}
if(temp&0x01!=0){
c=1;
}else{
c=0;
}
}
return source;
}
/*********************************
*
* @param source[]
* @param c 进位标志位
* @param n 数组长度
* @return source数组带进位左移
*
*********************************/
unsigned char * RLC(unsigned char source[],char c,char n)
{
int i=0;
unsigned char temp;
for(i=0;i0; i--)
{
nlf=NLF[getBit(source, 30)][getBit(source, 25)][getBit(source, 19)][getBit(source, 8)][getBit(source, 0)];
y15=getBit(source, 15);
y31=getBit(source, 31);
k=getBit(key, (i-1)%64);
result=nlf^y15^y31^k;
if (result!=0) {
c=1;
}else {
c=0;
}
source=RLC(source,c,4);
}
return source;
}
/*************************************
*
* 初始化非线性逻辑函数的值
*
*************************************/
void init()
{
NLF[0][0][0][0][0]=0;
NLF[0][0][0][0][1]=1;
NLF[0][0][0][1][0]=1;
NLF[0][0][0][1][1]=1;
NLF[0][0][1][0][0]=0;
NLF[0][0][1][0][1]=1;
NLF[0][0][1][1][0]=0;
NLF[0][0][1][1][1]=0;
NLF[0][1][0][0][0]=0;
NLF[0][1][0][0][1]=0;
NLF[0][1][0][1][0]=1;
NLF[0][1][0][1][1]=0;
NLF[0][1][1][0][0]=1;
NLF[0][1][1][0][1]=1;
NLF[0][1][1][1][0]=1;
NLF[0][1][1][1][1]=0;
NLF[1][0][0][0][0]=0;
NLF[1][0][0][0][1]=0;
NLF[1][0][0][1][0]=1;
NLF[1][0][0][1][1]=1;
NLF[1][0][1][0][0]=1;
NLF[1][0][1][0][1]=0;
NLF[1][0][1][1][0]=1;
NLF[1][0][1][1][1]=0;
NLF[1][1][0][0][0]=0;
NLF[1][1][0][0][1]=1;
NLF[1][1][0][1][0]=0;
NLF[1][1][0][1][1]=1;
NLF[1][1][1][0][0]=1;
NLF[1][1][1][0][1]=1;
NLF[1][1][1][1][0]=0;
NLF[1][1][1][1][1]=0;
}
int main()
{
unsigned char source[4];
unsigned char *p;
scanf("%c %c %c %c",&source[3],&source[2],&source[1],&source[0]);
p=source;
printf("%x %x %x %x\n",p[3],p[2],p[1],p[0]);
p=CRYPT(p);
printf("%x %x %x %x\n",p[3],p[2],p[1],p[0]);
p=DECRYPT(p);
printf("%x %x %x %x",p[3],p[2],p[1],p[0]);
return 0;
}
源码三:KeeLoqCrypt.java
import java.util.Scanner;
public class KeeLoqCrypt {
/**
* @param args
*/
private static long SERX=0xefcdab2143658709L;
private static long key=0Xefcdab2143658709L;
private static int NLF[][][][][]=new int[2][2][2][2][2];
/*********
* 构造函数
*/
KeeLoqCrypt(){
NLF[0][0][0][0][0]=0;
NLF[0][0][0][0][1]=1;
NLF[0][0][0][1][0]=1;
NLF[0][0][0][1][1]=1;
NLF[0][0][1][0][0]=0;
NLF[0][0][1][0][1]=1;
NLF[0][0][1][1][0]=0;
NLF[0][0][1][1][1]=0;
NLF[0][1][0][0][0]=0;
NLF[0][1][0][0][1]=0;
NLF[0][1][0][1][0]=1;
NLF[0][1][0][1][1]=0;
NLF[0][1][1][0][0]=1;
NLF[0][1][1][0][1]=1;
NLF[0][1][1][1][0]=1;
NLF[0][1][1][1][1]=0;
NLF[1][0][0][0][0]=0;
NLF[1][0][0][0][1]=0;
NLF[1][0][0][1][0]=1;
NLF[1][0][0][1][1]=1;
NLF[1][0][1][0][0]=1;
NLF[1][0][1][0][1]=0;
NLF[1][0][1][1][0]=1;
NLF[1][0][1][1][1]=0;
NLF[1][1][0][0][0]=0;
NLF[1][1][0][0][1]=1;
NLF[1][1][0][1][0]=0;
NLF[1][1][0][1][1]=1;
NLF[1][1][1][0][0]=1;
NLF[1][1][1][0][1]=1;
NLF[1][1][1][1][0]=0;
NLF[1][1][1][1][1]=0;
}
/*****************
*
* @param source
* @param n
* @return source的第n个位数
*/
private static int getBit(long source,int n) {
long temp0=((long) 1<>1)|0x80000000;
}else{
soucre=(soucre>>1)&0x7fffffff;
}
return soucre;
}
/********************
*
* @param source
* @param c
* @return 带进位左移
*/
private static int RLC(int source, int c){
if(c!=0){
source=(source<<1)|1;
}else{
source=(source<<1)&0xFFFFFFFE;
}
return source;
}
/********************
*
* @param source
* @param key
* @return source经过key密钥进行KeeLoq加密后的数据
*/
private static int CRYPT(int source , long key) {
long mKey=key;
int c;
for (int i = 0; i < 528; i++) {
int nlf=NLF[getBit(source, 31)][getBit(source, 26)][getBit(source, 20)][getBit(source, 9)][getBit(source, 1)];
int y16=getBit(source, 16);
int y0=getBit(source, 0);
int k=getBit(mKey, i%64);
int result=nlf^y16^y0^k;
if (result!=0) {
c=1;
}else {
c=0;
}
source=RRC(source,c);
}
return source;
}
/*********************************
*
* @param source
* @param key
* @return source经过key密钥进行KeeLoq解密后的数据
*/
private static int DECRYPT(int source , long key) {
long mkey=key;
int c;
for (int i = 528; i >0; i--) {
int nlf=NLF[getBit(source, 30)][getBit(source, 25)][getBit(source, 19)][getBit(source, 8)][getBit(source, 0)];
int y15=getBit(source, 15);
int y31=getBit(source, 31);
int k=getBit(mkey, (i-1)%64);
int result=nlf^y15^y31^k;
if (result!=0) {
c=1;
}else {
c=0;
}
source=RLC(source,c);
}
return source;
}
public static void main(String[] args) {
// TODO Auto-generated method stub
NLF[0][0][0][0][0]=0;
NLF[0][0][0][0][1]=1;
NLF[0][0][0][1][0]=1;
NLF[0][0][0][1][1]=1;
NLF[0][0][1][0][0]=0;
NLF[0][0][1][0][1]=1;
NLF[0][0][1][1][0]=0;
NLF[0][0][1][1][1]=0;
NLF[0][1][0][0][0]=0;
NLF[0][1][0][0][1]=0;
NLF[0][1][0][1][0]=1;
NLF[0][1][0][1][1]=0;
NLF[0][1][1][0][0]=1;
NLF[0][1][1][0][1]=1;
NLF[0][1][1][1][0]=1;
NLF[0][1][1][1][1]=0;
NLF[1][0][0][0][0]=0;
NLF[1][0][0][0][1]=0;
NLF[1][0][0][1][0]=1;
NLF[1][0][0][1][1]=1;
NLF[1][0][1][0][0]=1;
NLF[1][0][1][0][1]=0;
NLF[1][0][1][1][0]=1;
NLF[1][0][1][1][1]=0;
NLF[1][1][0][0][0]=0;
NLF[1][1][0][0][1]=1;
NLF[1][1][0][1][0]=0;
NLF[1][1][0][1][1]=1;
NLF[1][1][1][0][0]=1;
NLF[1][1][1][0][1]=1;
NLF[1][1][1][1][0]=0;
NLF[1][1][1][1][1]=0;
Scanner mScanner=new Scanner(System.in);
int HOPE=mScanner.nextInt(16);
System.out.printf("%x\n",CRYPT(HOPE,key));
System.out.printf("%x\n",DECRYPT(CRYPT(HOPE,key),key));
System.out.printf("%x\n",getBit(HOPE,1));
}
}
请支持原创,尊重原创,转载请注明出处:http://blog.csdn.net/kangweijian(来自kangweijian的csdn博客)
by 2015.2.4晚