张友正相机标定法以及Matlab工具包实现Camera calibration
一.相机的参数
1.两个坐标系
世界坐标系（world coordinate）(xw,yw,zw)，也称为测量坐标系，是一个三维直角坐标系，以其为基准可以描述相机和待测物体的空间位置。世界坐标系的位置可以根据实际情况自由确定。
相机坐标系（camera coordinate）(xc,yc,zc)，也是一个三维直角坐标系，原点位于镜头光心处，x、y轴分别与相面的两边平行，z轴为镜头光轴，与像平面垂直。
2.相机的内参数
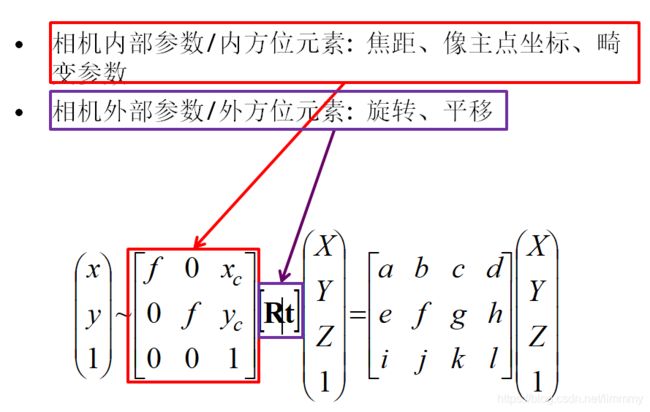
设P=(X,Y,Z)为场景中的一点，在针孔相机模型中，其要经过以下几个变换，最终变为二维图像上的像点p=(μ,ν)，将P从世界坐标系通过刚体变换(旋转和平移)变换到相机坐标系，这个变换过程使用的是相机间的相对位姿，也就是相机的外参数。
从相机坐标系，通过透视投影变换到相机的成像平面上的像点p=(x,y)。将像点p从成像坐标系，通过缩放和平移变换到像素坐标系上点p=(μ,ν) 。
相机将场景中的三维点变换为图像中的二维点，也就是各个坐标系变换的组合，可将上面的变换过程整理为矩阵相乘的形式：
将矩阵K称为相机的内参数,
其中，α,β表示图像上单位距离上像素的个数，则fx=αf,fy=βf将相机的焦距f，变换为在x,y方向上像素度量表示。另外，为了不失一般性，可以在相机的内参矩阵上添加一个扭曲参数γ，该参数用来表示像素坐标系两个坐标轴的扭曲。则内参数K变为
空间到图像的映射可以表示为
其中H是描述Homographic矩阵，可以通过最小二乘得到，从角点世界坐标系到图像坐标的关系求解。对一个给定的单应性矩阵，对内参有两个基本的约束条件，因为这个矩阵由8个自由度和6个外部参数（3个是旋转矩阵和3个是平移向量的），此时我们只能得到两个内参的约束条件。
二.张正友平面的相机标定方法
以下内容参考这篇论文解读：SLAM入门之视觉里程计(6)：相机标定 张正友经典标定法详解
张正友标定法论文，原文为“Flexible camera calibration by viewing a plane from
unknown orientations”
在张氏标定法中，用于标定的棋盘格是三维场景中的一个平面π，其在成像平面的像是另一个平面π，知道了两个平面的对应点的坐标，就可以求解得到两个平面的单应矩阵H。其中，标定的棋盘格是特制的，其角点的坐标是已知的；图像中的角点，可以通过角点提取算法得到，这样就可以得到棋盘平面Π和图像平面π的单应矩阵H。
通过上面的相机模型有：
p = K [ R ∣ t ] P p=K[R|t]P p=K[R∣t]P
其中p是像点坐标，P是标定的棋盘坐标。 这样就可以得到下面的等式：
H = K [ R ∣ t ] H=K[R|t] H=K[R∣t]
H表示的是成像平面和标定棋盘平面之间的单应矩阵。通过对应的点对解得H后，则可以通过上面的等式得到相机的内参数K，以及外参旋转矩阵R和平移向量t。
步骤：
- 给出一个封闭解
- 根据最大似然估计给出非线性的最优解
- 考虑透镜的径向畸变，给出解析解和非线性解
1.给出一个封闭解
定义一个矩阵B
注意，矩阵B是一个对称矩阵，其未知量只有6个，将6个未知量写为向量的形式
令hi为单应矩阵H的第i个行向量，则有
所以有：
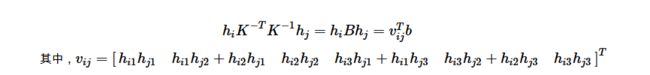
有了上边的等式，再来看从一幅标定板图像得到的等式
写成矩阵的形式有：
上面的一幅标定板图像取得的约束等式，假如有n幅图像，则
V b = 0 Vb=0 Vb=0
其中，V是一个2n×6的矩阵，b是一个6维向量，所以
- 当n≥3，可以得到b的唯一解;
- 当n=2，则可以假设扭曲参数γ=0作为额外的约束条件
- 当n=1 ，则值能计算两个相机的内参数
对于方程Vb=0可以使用SVD求得其最小二乘解。
从而可以得到相机的各个内参数：（内部参数可以根据cholesky分解得到）
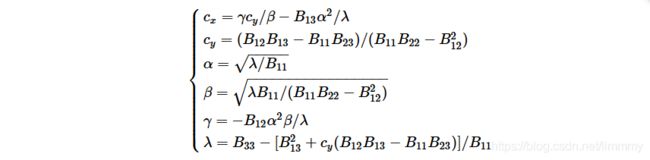外部参数可以根据Homography求解，
2.最大似然估计给出非线性的最优解
上面使用最小二乘法得到估计得到的解，并没有物理上的实际意义，。为了进一步增加标定结果的可靠性，可以使用最大似然估计(Maximum likelihood estimation)来优化上面估计得到的结果。假设同一相机从n个不同的角度的得到了n幅标定板的图像，每幅图像上有m个像点。Mij表示第i幅图像上第j个像点对应的标定板上的三维点，则
m^(K,Ri,ti,Mij)表示Mij的像点。其中，Ri,ti表示第i幅图像对应相机的旋转矩阵和平移向量，K是相机的内参数。则像点mij的概率密度函数是
构造似然函数
为了能够让L取得最大值，需要最小化下面的值
3.径向畸变的处理
到目前为止，并没有考虑相机的镜头畸变（由于在相机组装的过程中，透镜不能和成像平面严格平行，会引入切向畸变）。张氏标定法中只关注了影响较大的径向畸变。径向畸变主要有两大类畸变：
- 透镜质量原因
- 光线在远离透镜中心的地方比靠近中心的地方更加弯曲（所以拍照的时候尽量不要站在镜头边缘不然脸会变形哈哈哈哈哈哈哈哈或）
设(μ,ν)是理想的无畸变的像素坐标；
(μ,ν)是畸变后的像素坐标；
(μ0,ν0)是相机的主点；
(x,y)和(x,y)理想的无畸变的归一化的图像坐标和畸变后的归一化图像坐标，
使用下面的式子表示径向畸变：
k1,k2表示径向畸变的系数。径向畸变的中心和相机的主心是在相同的位置，
假设γ=0，则有：
将上面的式子改写为矩阵的形式
上面的等式是从一幅图像上的一个点取得，设有n幅图像，每幅图像上有m个点，则将得到的所有等式组合起来，可以得到2mn个等式，将其记着矩阵形式
D k = d Dk=d Dk=d
则可得
和上面类似利用最大似然估计取得最优解，使用LM的方法估计使得下面式子是最小值的参数值
得到畸变参数k1,k2后，可以先将图像进行去畸变处理，然后用去畸变后的图像坐标估计相机的内参数。
三.用Matlab的工具包进行相机参数标定
步骤如下：
1. 去Matlab官网下载工具包（toolbox_calib）的压缩文件，并将其解压到
D:\MATLAB\MATlabR2017b\toolbox\
2. 在Matlab里找到这个路径并保存
3. 选择“calib_gui.m”文件并打开运行，出现下图GUI界面，选择第一行Standard
4. 选择Image names
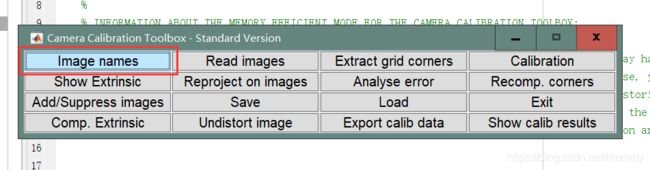
输入校准图像的基本名称（Image）和图像格式（jpg）。 然后将所有图像（其中的20个）加载到变量 I_1， I_2，…， I_20中的内存中（通过命令读取自动执行的图像）。图像的数量存储在变量 n_ima（此处为= 20）中。
输入Basename：Image（我的图像命名规则是Image1.jpg）以及图像类型：jpg。读入我的20张图像。
此图像始终可以通过运行“ mosaic.m”重新生成
5. 然后再回到GUI，选择Extract grid corners，进行角点提取。
按“enter”（带有空参数）默认设置就行，主要是选择图像、选择搜索窗口的大小。
当使用大量图像时，该工具特别方便，因为用户不必手动输入图案的x和y方向上的方块数。但是，在某些非常罕见的情况下，此代码可能无法预测正确的方块数。这通常在校准具有极端扭曲的镜头时发生。
输入Y方向和X方向的棋盘格子数目
我的棋盘格子是2015的，对应输入，其余选项为默认（enter即可）
手动标定坐标轴，然后检测角点位置。输入XY的格子数以及画出棋盘范围是为了更好的找到有效的角点，重复20次（取决于你图片的数量）
然后自动提取图像角点，并在图3中显示（角点周围的蓝色方块显示角落取景窗口的极限）：
如果预测的角落接近实际图像角落，则可以跳过以下步骤（如果没有太多的图像失真）。这是当前图像的情况：预测的角落足够接近真实图像角落。因此，没有必要通过输入径向畸变系数的猜测来“帮助”软件检测图像拐角。按“enter”，使用这些位置作为初始猜测自动提取角。
6.
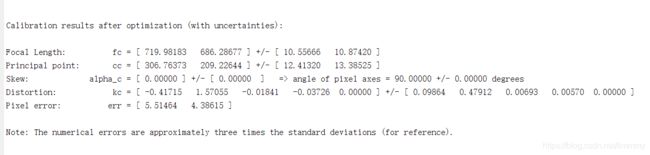优化后的校准结果（有不确定性）：
焦距：fc = [719.98183 686.28677] +/- [10.55666 10.87420]
要点：cc = [306.76373 209.22644] +/- [12.41320 13.38525]
偏斜：alpha_c = [0.00000] +/- [0.00000] =>像素轴角= 90.00000 +/- 0.00000度
失真：kc = [-0.41715 1.57055 -0.01841 -0.03726 0.00000] +/- [0.09864 0.47912 0.00693 0.00570 0.00000]
像素错误：错误= [5.51464 4.38615]
注意：数值误差约为标准偏差的三倍（供参考）。
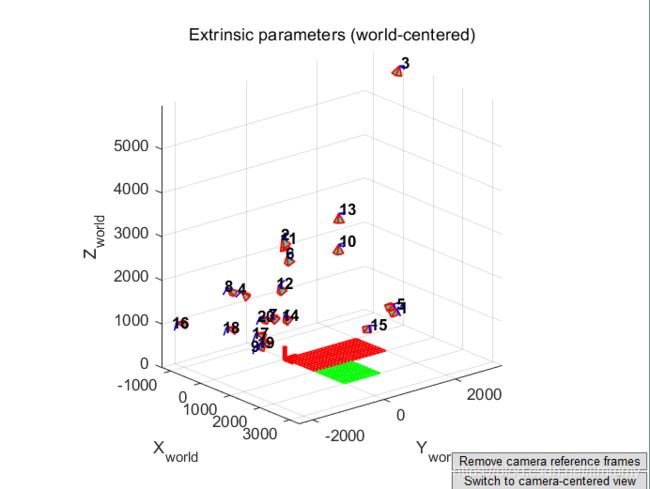
6.单击Camera校准工具中的Show Extrinsic。
以3D图的形式显示外部参数（网格相对于相机的相对位置）
拍摄时第三张就是较远拍摄的，第十张是平行拍摄。
转换成世界坐标系来看，在该图中，帧 （O c，X c，Y c，Z c）是相机参考帧。红色金字塔对应于由图像平面定义的相机的有效视野。
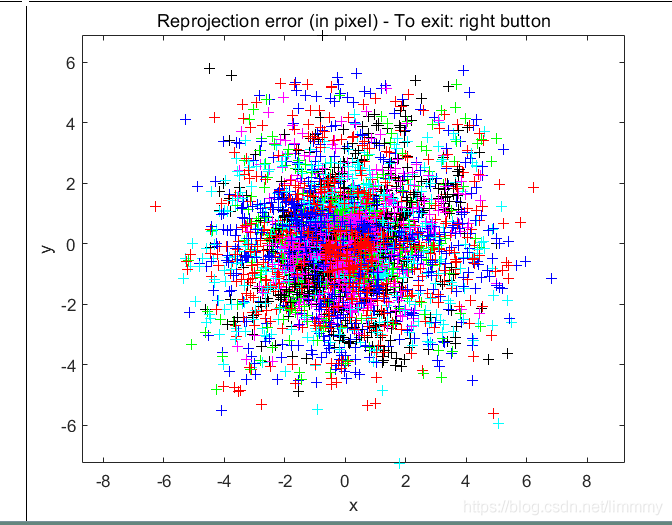
7.
请注意大量数字中的重投影错误非常大。原因是我们在一些高度扭曲的图像上提取角落时没有做过非常谨慎的工作（通过使用预测的失真选项可以做得更好）。尽管如此，我们现在可以通过自动重新计算所有图像上的图像角来进行校正。
alibration results after optimization (with uncertainties):
Focal Length: fc = [ 715.12336 686.47813 ] +/- [ 3.63160 3.70397 ]
Principal point: cc = [ 305.61566 218.96868 ] +/- [ 5.08350 4.64733 ]
Skew: alpha_c = [ 0.00000 ] +/- [ 0.00000 ] => angle of pixel axes = 90.00000 +/- 0.00000 degrees
Distortion: kc = [ -0.33331 1.36677 -0.00990 -0.04262 0.00000 ] +/- [ 0.03520 0.17249 0.00249 0.00241 0.00000 ]
Pixel error: err = [ 1.77604 1.63378 ]
Note: The numerical errors are approximately three times the standard deviations (for reference).
迭代检测多次后结果稳定如下：
Calibration results after optimization (with uncertainties):
Focal Length: fc = [ 688.79379 676.37139 ] +/- [ 3.34412 3.47598 ]
Principal point: cc = [ 321.62192 233.97302 ] +/- [ 4.73725 4.37314 ]
Skew: alpha_c = [ 0.00000 ] +/- [ 0.00000 ] => angle of pixel axes = 90.00000 +/- 0.00000 degrees
Distortion: kc = [ -0.20336 1.06436 -0.00338 -0.04251 0.00000 ] +/- [ 0.03475 0.15950 0.00266 0.00296 0.00000 ]
Pixel error: err = [ 1.71202 1.52665 ]
Note: The numerical errors are approximately three times the standard deviations (for reference).
结果显示我的手机的内参矩阵为
K = ( f 0 x 0 0 f y 0 0 0 1 ) = ( 688.79379 0 321.62192 0 676.37139 233.97302 0 0 1 ) K=\begin{pmatrix} f & 0 & x_{0}\\ 0 & f & y_{0}\\ 0 & 0 & 1 \end{pmatrix}=\begin{pmatrix} 688.79379 & 0 & 321.62192\\ 0 & 676.37139 & 233.97302\\ 0 & 0 & 1 \end{pmatrix} K=⎝⎛f000f0x0y01⎠⎞=⎝⎛688.79379000676.371390321.62192233.973021⎠⎞
参考文章：
- 张正友标定法译文
- 张正友标定法原理
- Matlab官网相机检测工具包的使用方法