七、数字图像处理之频域处理（2）

（一）在频域中直接生成滤波器

（1）建立网格数组以实现频域滤波器

在这篇博客中，主要写的是循环对称滤波器，它们是由距滤波器中心点的距离的不同函数规定的。为实现这些滤波器而开发的M-函数是基础，并且可以很容易地推广到相同结构的其他函数中。

在上一篇博客中运用到了dftuv的M-函数，这用于生成网格数组来实现频域滤波器。

function [U,V] = dftuv(M,N)   % dftuv的M-函数
u = single(0:(M-1));  
v = single(0:(N-1));    %建立变量范围
idx = find(u >M/2);   
u(idx) = u(idx) - M;
idy = find(v >N/2);
v(idy) = v(idy) - N;  %计算在meshgrid中使用的索引
[V,U] = meshgrid(v,u);   %计算在meshgrid中行列

调用dftuv函数：

[U,V]=dftuv(8,5);
DSQ= U.^2+V.^2
fftshift(DSQ)    %使用函数 fftshift 得到频域矩形中心的距离

实验结果：

fftshift(DSQ) 结果，如图：

（2）频域低通（平滑）滤波器

实验代码：

f = imread('C:\Users\Public\Pictures\Sample Pictures\Fig0313(a).tif ');
[f,revertclass] = tofloat(f);
PQ = paddedsize(size(f));
[U,V] = dftuv(PQ(1),PQ(2));
D = hypot(U,V);
D0 = 0.05*PQ(2);
F = fft2(f,PQ(1),PQ(2)); 
H = exp(-(D.^2)/(2*(D0^2)));
g = dftfilt(f,H);
g = revertclass(g);
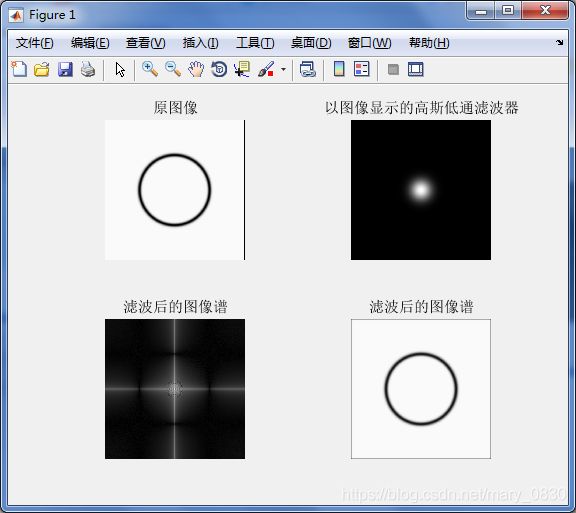
subplot(221),imshow(f), title('原图像');
subplot(222),imshow(fftshift(H)), title('以图像显示的高斯低通滤波器');
subplot(223),imshow(log(1+abs(fftshift(F))),[]), title('滤波后的图像谱');
subplot(224),imshow(g), title('滤波后的图像谱');

实验结果：

实验结论：
通过上述两幅图片的比较，低通（平滑）滤波器的作用是平滑图像，但是会模糊图像。以上的实验代码可以说明此代码可以用于灰度图像的平滑图像。

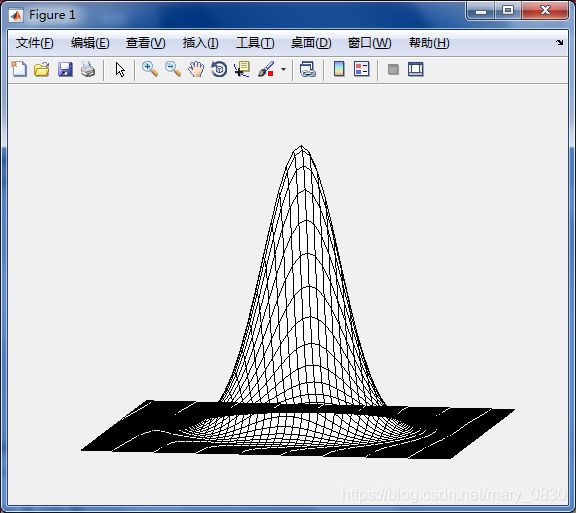
（3）线框及表面绘制

说明：下面将介绍3D线框及表面的绘制，基本语法如下：

mesh(H)  
mesh(H(1:k:end,1:k:end))       %用于绘制第k个点
colormap([0 0 0])            %用于设置线框颜色（[0 0 0]黑色，默认值是彩色线框）
gird off                    %关掉网格命令
axis off            %关掉轴的命令
view(az,el)     %设置观察者位置

实验代码：

H = fftshift(lpfilter('gaussian',500,500,50));
mesh(double(H(1:10:500,1:10:500)))

实验结果：

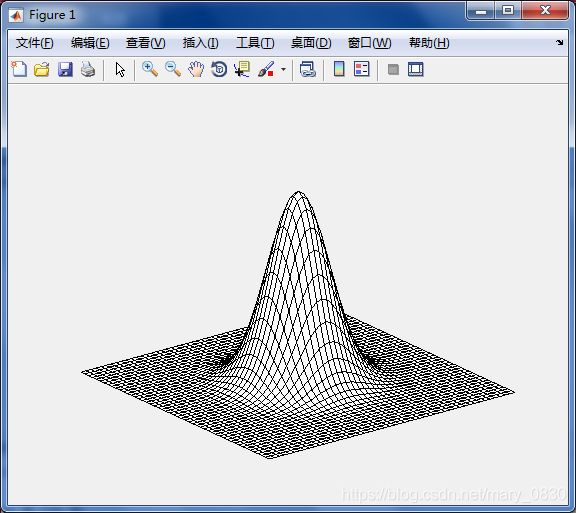
实验代码：

H = fftshift(lpfilter('gaussian',500,500,50));
mesh(double(H(1:10:500,1:10:500)))    %建立线框图
axis tight           % 产生线框图
colormap([0 0 0])     %将线框颜色变成黑色

实验结果：

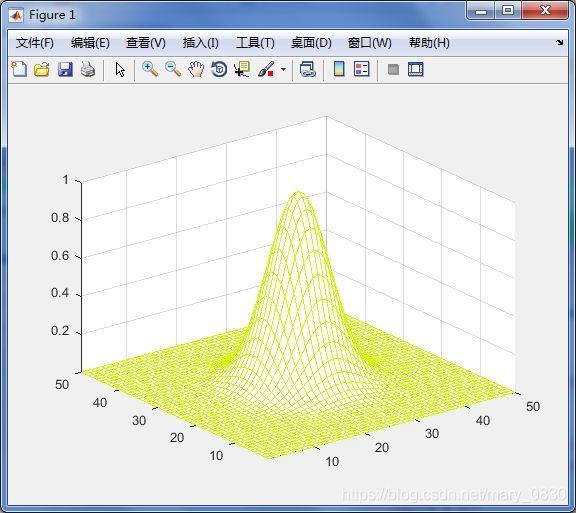
实验代码：

colormap([0 1 0])     %将线框颜色变成绿色，三个数字分别表示红绿蓝，且colormap的值必须位于【0,1】之间。

实验代码：

colormap([0.8 1 0])     %将线框颜色变成淡黄色

实验代码：

H = fftshift(lpfilter('gaussian',500,500,50));
mesh(double(H(1:10:500,1:10:500)))
axis tight
colormap([0 0 0])
axis off         %消除坐标轴
grid off        %消除栅格

实验代码：

H = fftshift(lpfilter('gaussian',500,500,50));
mesh(double(H(1:10:500,1:10:500)))
axis tight           %设置坐标轴显示范围为紧凑型 
colormap([0 0 0])
axis off 
grid off
view(-25,0)        %将观察者的视角设置为方位角为-25且仰角设置为0

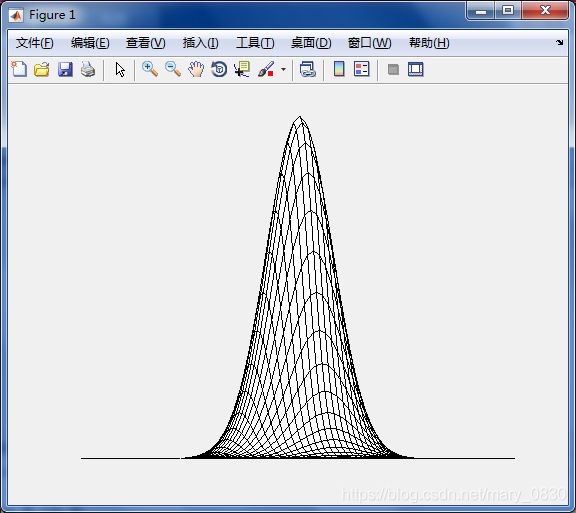
实验代码：

view(-10,-10)      %将观察者的视角设置为方位角为-10且仰角设置为-10

有时候用surf函数可以绘制表面图：

surf(H)

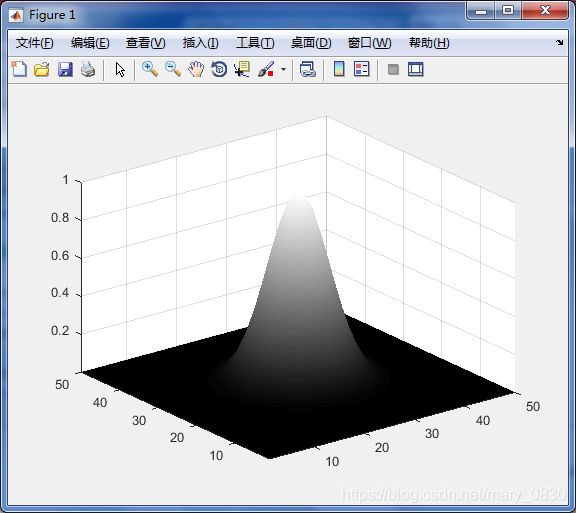
实验代码：

H = fftshift(lpfilter('gaussian',500,500,50));
surf(double(H(1:10:500,1:10:500)));
axis tight
colormap(gray)           %将颜色转为灰度
shading interp           %平滑小面描影和消除栅网线
[Y,X] = meshgrid(-2:0.1:2,-2:0.1:2);   %用于产生坐标值
Z = X.*exp(-X.^2 - Y.^2);

实验结果：

实验结论：
函数mesh是用来显示线框图，而surf是用于显示表面图。

（二）高通（锐化）频域滤波器

高通滤波器函数hpfilter：

function H = hpfilter(type, M, N, D0, n)
if nargin == 4
    n = 1; %默认值为1
end
Hlp = lpfilter(type,M,N,D0,n);
H = 1-Hlp;

实验代码：

H1 = fftshift(hpfilter('ideal',500,500,50));
H2 = fftshift(hpfilter('gaussian',500,500,50));
H3 = fftshift(hpfilter('btw',500,500,50));
mesh(double(H1(1:10:500,1:10:500)));
mesh(double(H2(1:10:500,1:10:500)));
mesh(double(H3(1:10:500,1:10:500)));
axis tight
axis off
subplot(131),imshow(H1), title('理想高通滤波器');
subplot(132),imshow(H2), title('高斯高通滤波器');
subplot(133),imshow(H3), title('巴特沃斯高通滤波器');

实验结果：

实验代码：

f = imread('C:\Users\Public\Pictures\Sample Pictures\flower.jpg ');
PQ = paddedsize(size(f));
D0 = 0.05*PQ(1);
H = hpfilter('ideal',PQ(1),PQ(2),D0);
g = dftfilt(f,H);
subplot(121),imshow(f),title('原始图像');
subplot(122),imshow(g,[]),title('理想高通滤波器后的图像');

实验结果：
（图一）

（图二）

实验代码：

f = imread('C:\Users\Public\Pictures\Sample Pictures\flower.jpg ');
PQ = paddedsize(size(f));
D0 = 0.05*PQ(1);
H = hpfilter('btw',PQ(1),PQ(2),D0);
g = dftfilt(f,H);
subplot(121),imshow(f),title('原始图像');
subplot(122),imshow(g,[]),title('巴特沃斯高通滤波器后的图像');

实验结果：
（图三）

>> f = imread('C:\Users\Public\Pictures\Sample Pictures\timg.jpg ');
>> PQ = paddedsize(size(f));
D0 = 0.05*PQ(1);
H = hpfilter('ideal',PQ(1),PQ(2),D0);
g = dftfilt(f,H);
subplot(121),imshow(f),title('原始图像');
subplot(122),imshow(g,[]),title('理想高通滤波器后的图像');

（图四）

实验结论： 对比图一和图二，不同图像的高斯高通滤波器滤除的边缘有差异，高斯高通滤波器很明显的可以显示出图像的边缘。对比图一和图三，巴特沃斯比高斯滤出的边缘细节更多。对比图二和图四，使用理想高通滤波器的图像产生了振铃效应。理想滤波器的特性通常用来解释振铃现象。 图像处理中，对一幅图像进行滤波处理，若选用的频域滤波器具有陡峭的变化，则会使滤波图像产生“振铃”。振铃就像是一块石头投进水中，产生一波一波的水纹。
这三种滤波方式用于不同的情况，若需要更多细节，可以用理想或者巴特沃斯，但理想滤波器会产生振铃效应；若只需要边界，可以用巴特沃斯或者高斯。

（三）选择性滤波

（1）带通和带阻滤波器

function H = bandfilter(type,band,M,N,D0,W,n)
if nargin < 7
    n = 1;  %默认值
end
switch lower(type)
    case 'ideal'
        H = idealReject(D,D0,W);
    case 'btw'
        H = btwReject(D,D0,W,n);
    case 'gaussian'
        H = gaussianReject(D,D0,W);
    otherwise
        error('Unknown filter type.')
end

if strcmp(band,'pass')
    H = 1 - h;
end

%------------------------------------------------------------------%
function H = idealReject(D,D0,W)
RI = D <= D0 - (W/2);
RO = D >= D0 + (W/2);
H = tofloat(RO|RI);
%------------------------------------------------------------------%
function H = btwReject(D,D0,W,n)
H = 1./(1 + ((D*W)./(D.^2 - D0^2)).^2*n));
%------------------------------------------------------------------%
function H = gaussianReject(D,D0,W)
H = 1 - exp(-((D.^2 - D0^2)./(D.*W + eps)).^2);

（2）陷波带阻和陷波带通滤波器

说明：陷波滤波器是更加有用的选择性滤波器。

实验代码：使用陷波滤波器减少波纹

f = imread('C:\Users\Public\Pictures\Sample Pictures\flower.jpg ');
f=rgb2gray(f);   
[M,N] = size(f);
[f,revertclass] = tofloat(f);
F = fft2(f);
S = fftshift(log(1+abs(F)));    %将直流分量移到频谱中心
S = gscale(S);   %频谱
subplot(221),imshow(f),title('原图像');
subplot(222),imshow(S),title('显示频谱图像');
C1 = [99 154;128 163];         %交互式的尖峰
H1 = cnotch('gaussian', 'reject',M,N,C1,5);      %陷波滤波器
P1 = gscale(fftshift(H1).*(tofloat(S)));         %计算滤波器变换的频谱
subplot(223),imshow(P1), title('滤波变换的频谱图像');
g1 = dftfilt(f,H1);       %滤波图像
g1=revertclass(g1);
subplot(224),imshow(g1), title('滤波图像');

函数gscale：

function g=gscale(f,varargin)
if length(varargin)==0
  method='full8';
else method=varargin{1};
end
if strcmp(class(f),'double')&(max(f(:))>1 | min(f(:))<0)
   f=mat2gray(f);
end

switch method
case 'full8'
        g=im2uint8(mat2gray(double(f)));
case 'full16'
        g=im2uint16(mat2gray(double(f)));
case 'minmax'
       low = varargin{2};high = varargin{3};
       if low>1 | low<0 |high>1 | high<0
             error('Parameters low and high must be in the range [0,1]')
       end
       if strcmp(class(f),'double')
            low_in=min(f(:));
            high_in=max(f(:));
       elseif  strcmp(class(f),'uint8')
            low_in=double(min(f(:)))./255;
            high_in=double(max(f(:)))./255;
       elseif   strcmp(class(f),'uint16')
            low_in=double(min(f(:)))./65535;
            high_in=double(max(f(:)))./65535;
       end
       
       g=imadjust(f,[low_in high_in],[low high]);
otherwise
       error('Unknown method')
end

实验结果：
（图五）

（图六）

实验结论：
从图五和图六可以很明显的看出，滤波后的图像波纹减少了，而且图像更加明亮，基本上与原图像没有差别，因此实验证明自适应滤波器的滤波效果更好一些。
从上述图一至图六的对比可以看出，理想高通滤波器会产生振铃效应，滤波效果并不是很好，有点生硬；巴特沃斯高通滤波器和高斯高通滤波器不会产生振铃效应，滤波效果比理想高通滤波器更好一些。但若是加上自适应滤波器，自适应滤波器更加符合我们对图像的处理，因此自适应滤波器会更加普遍。