网络流增广路Edmonds-Karp算法 与 Dinic算法
https://www.luogu.org/problemnew/show/P3376
题目描述
如题,给出一个网络图,以及其源点和汇点,求出其网络最大流。
输入输出格式
输入格式:第一行包含四个正整数N、M、S、T,分别表示点的个数、有向边的个数、源点序号、汇点序号。
接下来M行每行包含三个正整数ui、vi、wi,表示第i条有向边从ui出发,到达vi,边权为wi(即该边最大流量为wi)
输出格式:一行,包含一个正整数,即为该网络的最大流。
输入输出样例
输入样例#1:
复制
4 5 4 3 4 2 30 4 3 20 2 3 20 2 1 30 1 3 40
输出样例#1:
复制
50
说明
时空限制:1000ms,128M
数据规模:
对于30%的数据:N<=10,M<=25
对于70%的数据:N<=200,M<=1000
对于100%的数据:N<=10000,M<=100000
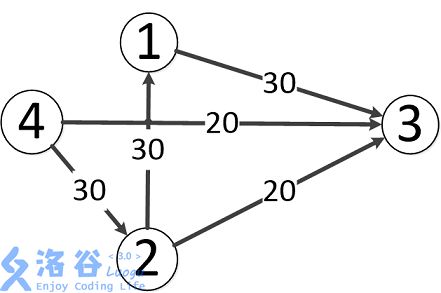
样例说明:
题目中存在3条路径:
4-->2-->3,该路线可通过20的流量
4-->3,可通过20的流量
4-->2-->1-->3,可通过10的流量(边4-->2之前已经耗费了20的流量)
故流量总计20+20+10=50。输出50。
EK
#include
#include
#include
#include
#include
using namespace std;
const int MAXN = 10000;
const int MAXM = 100000;
const int INF = 1E9;
typedef long long LL;
typedef double DB;
inline int get(){
char c;
while((c = getchar()) < '0' || c > '9');
int cnt = c - '0';
while((c = getchar()) >= '0' && c <= '9') cnt = cnt * 10 + c - '0';
return cnt;
}
int N,M,S,T;
struct edge{
int from,to,cap;
edge(int u,int v,int x): from(u),to(v),cap(x){}
};
vector e;
vector g[MAXN + 10];
int p[MAXN + 10];
int a[MAXN + 10];
void add_edge(int u,int v,int x){
e.push_back(edge(u,v,x));
e.push_back(edge(v,u,0));
int m = e.size();
g[u].push_back(m - 2);
g[v].push_back(m - 1);
}
int max_flow(int Sat,int End){
int flow = 0;
while(1){
memset(a,0,sizeof(a));
queue q;
q.push(Sat);
a[Sat] = INF;
while(!q.empty()){
int f = q.front(); q.pop();
for(int i = 0; i < g[f].size(); i ++){
edge k = e[g[f][i]];
if(!a[k.to] && k.cap > 0){
a[k.to] = min(k.cap,a[f]);
p[k.to] = g[f][i];
q.push(k.to);
}
}
if(a[End]) break;
}
if(!a[End]) break;
for(int i = End; i != Sat; i = e[p[i]].from){
e[p[i]].cap -= a[End];
e[p[i]^1].cap += a[End];
}
flow += a[End];
}
return flow;
}
int main(){
#ifdef lwy
freopen("1.txt","r",stdin);
/* #else
freopen(".in","r",stdin);
freopen(".out","w",stdout);*/
#endif
N = get(); M = get(); S = get(); T = get();
for(int i = 1; i <= M; i ++){
int u,v,x;
u = get(); v = get(); x = get();
add_edge(u,v,x);
}
printf("%d",max_flow(S,T));
return 0;
}
dinic
用bfs建立层次图(按深度),流量为0的边不加以考虑,这样每次bfs完如果能到T,那么就存在增广路。
以bfs建立的层次图进行dfs,寻找增广路。
重复上述过程直到找不到增广路,即求出最大流。
dfs的终止条件是找到汇点或 a = 0 (a = 0 时说明已经增广了一条路,且之后的增广不能再通过这条路,如果继续增广,后面的搜索都是无效的,所以要回溯更新每条边的残量,直到更新到最小残量时则继续搜索,因为a(最小残量)已经更新,当a = 0 时会再次回溯)。
这里cur[] 的作用是记录上次考虑的弧,这样回溯后再进行搜索的时候就可以避免重复搜索。
#include
#include
#include
#include
#include
#include
using namespace std;
const int MAXN = 100000;
const int INF = 1E9;
typedef long long LL;
typedef double DB;
inline int get(){
char c;
while((c = getchar()) < '0' || c > '9');
int cnt = c - '0';
while((c = getchar()) >= '0' && c <= '9') cnt = cnt * 10 + c - '0';
return cnt;
}
struct edge{
int fr,to,res;
edge(int u,int v,int f):fr(u),to(v),res(f){};
};
vector e;
vector g[MAXN + 10];
int dep[MAXN + 10];
int cur[MAXN + 10];
bool vis[MAXN + 10];
int N,M,S,T,maxf;
inline bool bfs(){
memset(vis,0,sizeof(vis));
queue q;
q.push(S);
dep[S] = 0; vis[S] = 1;
while(!q.empty()){
int f = q.front(); q.pop();
for(int i = 0; i < g[f].size(); i ++){
edge k = e[g[f][i]];
if(!vis[k.to] && k.res > 0){
vis[k.to] = true;
dep[k.to] = dep[f] + 1;
q.push(k.to);
}
}
}
return vis[T];
}
inline int dfs(int x,int a){
if(x == T || a == 0) return a;
int flowt = 0,flown;
for(int& i = cur[x]; i < g[x].size(); i ++){
edge k = e[g[x][i]];
if(dep[x] + 1 == dep[k.to]){//
flown = dfs(k.to,min(a,k.res));
if(flown > 0){
e[g[x][i]].res -= flown;
e[g[x][i]^1].res += flown;
flowt += flown;
a -= flown;
if(a == 0) break;
}
}
}
return flowt;
}
int main(){
#ifdef lwy
freopen("1.txt","r",stdin);
/* #else
freopen(".in","r",stdin);
freopen(".out","w",stdout); */
#endif
N = get(); M = get(); S = get(); T = get();
for(int i = 1; i <= M; i ++){
int u,v,f;
u = get(); v = get(); f = get();
e.push_back(edge(u,v,f));
e.push_back(edge(v,u,0));
int m = e.size();
g[v].push_back(m - 1);
g[u].push_back(m - 2);
}
while(bfs()){
memset(cur,0,sizeof(cur));
maxf += dfs(S,INF);
}
printf("%d",maxf);
return 0;
}