论文笔记：Faster R-CNN: Towards Real-Time Object Detection with Region Proposal Networks

一、基本信息

标题：Faster R-CNN: Towards Real-Time Object Detection with Region Proposal Networks
时间：2016
引用格式：Ren, Shaoqing, et al. “Faster r-cnn: Towards real-time object detection with region proposal networks.” Advances in neural information processing systems. 2015.

二、研究背景

Fast R-CNN已经比R-CNN块很多。但是，Fast R-CNN还是用Selective Search方法计算候选区域region proposals，这就导致在选择region proposals上的瓶颈。本文提出使用RPN全卷积网络预测Anchors

三、创新点

网络结构

Fast R-CNN：

Faster R-CNN：

网络结构的差别主要是在初始卷积层和ROI池化层中间，Fast R-CNN的ROI池化层的输入是由Selective Search方法计算候选区域region proposals的对应卷积后区域，而Faster R-CNN池化层的输入是由RPN网络得到region proposals的对应卷积后区域。下面主要介绍RPN网络。

---

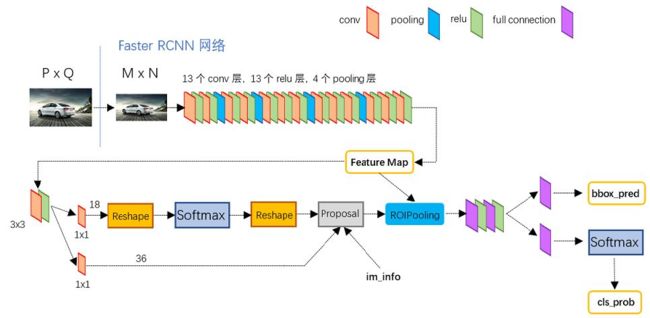
RPN得从Feature Map开始，也就是卷积层的输出，上图使用的是VGG16，输入图像经过13个conv层+13个relu层+4个pooling层。
那么Feature Map的大小是多少？

卷积层

所有的conv层都是：kernel_size=3，pad=1，stride=1 做的输same卷积操作，输出大小不变
所有的pooling层都是：kernel_size=2，pad=0，stride=2 池化输出大小减半
带入公式$\left(\frac{n+2p-f}{s}+1\right)\ast \left(\frac{n+2p-f}{s}+1\right)$验证也是一样的结果
具体卷积推算参考这个笔记

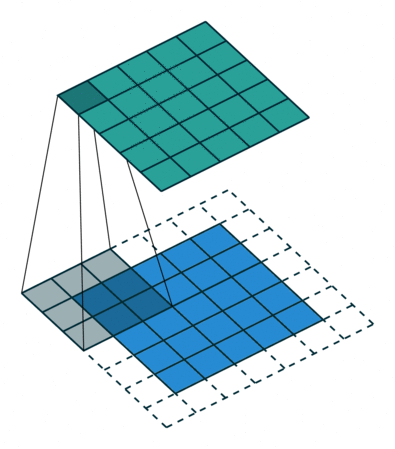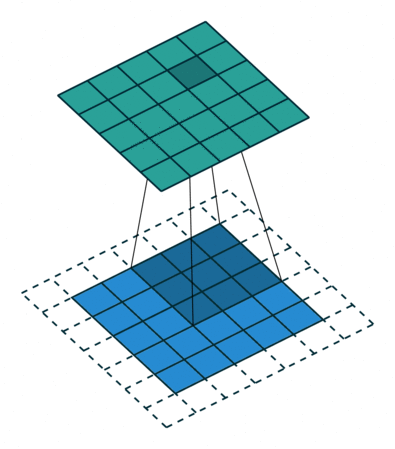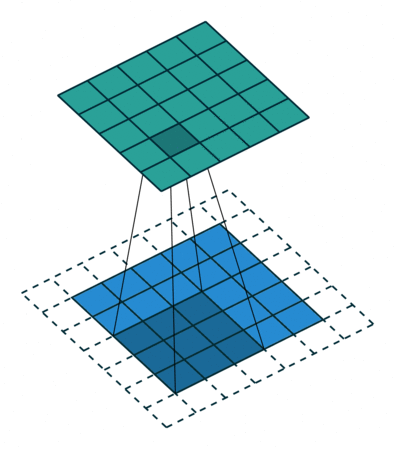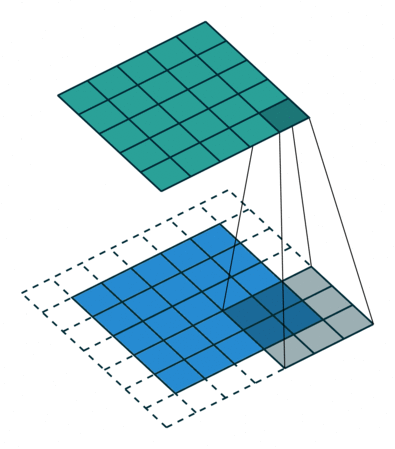
论文中会把图片resize到800 * 600也就是M=800 N=600。根据上面的推导，只有4个池化层改变了大小(通道数看最后一个卷积层的滤波器数目)，也就是最后输出的Feature Map为800/16 = 50 600/16=37.5~38，即50 * 38的大小

RPN(Region Proposal Networks)

上面说到Feature Map大小为50 * 38 ，通道数ZF模型为256，VGG为512
然后在每个点设置9个Anchor，也就是Anchors。所以最后就会有50 * 38 * 9 = 17100个Anchor。

9个Anchor怎么产生？

Anchor

Ancho的数据结构是这么定义的：
一个Anchor用$\left(x_1,y_1,x_2,y_2\right)$ 表示一个矩形左上和右下角点坐标，也就是用其表示一个粗略的Proposal。
一共有3个尺度也就是Anchor Sacles(8, 16, 32)，每个尺度又分为长宽比为 width:height $\in \{1:1,1:2,2:1\}$ 三种，也就是Aspect ratios(0.5, 1, 2)。所以9中的Anchor如下示意。

补充：

---

Anchor Sacles(8, 16, 32)，我之前一直以为1个Anchor的输入就是8 * 8 16 * 16 32 *32的Feature Map，其实不是，理解错了。。。

看了这篇博客，复述一下

注意输入到RPN网络前(输出Feature Map后)，要Feature Map进行3 * 3 卷积，同时不改变大小和通道数，目的是进一步集中特征信视野更广，为什么要这么做?

就是因为1个Anchor的输入就是一个Feature Map的点。它为了能过看的更广，因为Anchor其实就是1个bbox。但是这个bbox的大小提现不是在输入的size上(输入就是一个高维，视野广阔的点)，它的大小提现在$\left(x_1,y_1,x_2,y_2\right)$上，而reg layer就是根据回归再修正一下$\left(x_1,y_1,x_2,y_2\right)$。而$\left(x_1,y_1,x_2,y_2\right)$的初始值怎么产生，下面有说明。

---

那么Feature Map产生的Anchor如下：

RPN

产生了Anchors，下一步就是对其分类，从17100Anchors中选出合适的，作为Proposal。
这个预测Anchor是不是Proposal的网络就是RPN

可以看到有2个分支，左边分支a box-classification layer(cls) layer用于预测Anchor是否包含物体（背景为negative，物体为positive），所以又2k个scores。右侧a box-regression layer(reg) layer用于回归预测Anchor的四个值，即$\left(x_1,y_1,x_2,y_2\right)$ 表示一个矩形左上和右下角点坐标，所以有4k个coordinates。这一步提高了Anchor的精度，然后如果cls的输出positive，则Anchor就作为Proposal输出。

更详细的网络结构：

可以看到RPN网络实际分为2条线：
上面一条通过softmax分类anchors获得positive和negative分类
下面一条用于计算对于anchors的bounding box regression偏移量，以获得精确的proposal。
而最后的Proposal层则负责综合positive anchors和对应bounding box regression偏移量获取proposals，同时剔除太小和超出边界的proposals。其实整个网络到了Proposal Layer这里，就完成了相当于目标定位的功能。

softmax判定positive与negative

1 * 1卷积数目时18，即输出是18d的，因为1个点有9个Anchor，每个点有正负之分。所以一共有2 * k = 2* 9 = 18个scores。

softmax前后都接一个reshape layer这是caffe框架实现机制，具体原因参考一文读懂Faster RCNN

bounding box regression

bbox的边框回归，损失函数和Fast R-CNN一样用的是Smooth_L1
即：
$${\mathrm{smooth}}_{L_1}(x)=\{\begin{array}{ll}0.5x^2& \text{ if }|x|<1\\ |x|-0.5& \text{ otherwise }\end{array}$$

但是和Fast R-CNN不一样的是Faster R-CNN不是直接预测新的x，y，w，h，而是预测一种平移加缩放的微调关系，有这个关系得到新的x，y，w，h。因此就有损失函数：

$$L_{reg}=\sum _i^{n}smoot{h}_{L_1}(\left|t_i-t_i^{\ast }\right|)+\lambda ||W_{\ast }\Vert$$

$$t_i^{\ast }=d_{\ast }(A)=W_{\ast }^T\cdot \varphi (A)$$

其中，$W_{\ast }$就表示一种位移缩放的变换

$$\begin{array}{rl}{t}_{\mathrm{x}}& =\left(x-x_{\mathrm{a}}\right)/w_{\mathrm{a}},t_{\mathrm{y}}=\left(y-y_{\mathrm{a}}\right)/h_{\mathrm{a}}\\ t_{\mathrm{w}}& =\log \left(w/w_{\mathrm{a}}\right),t_{\mathrm{h}}=\log \left(h/h_{\mathrm{a}}\right)\\ t_{\mathrm{x}}^{\ast }& =\left(x^{\ast }-x_{\mathrm{a}}\right)/w_{\mathrm{a}},t_{\mathrm{y}}^{\ast }=\left(y^{\ast }-y_{\mathrm{a}}\right)/h_{\mathrm{a}}\\ t_{\mathrm{w}}^{\ast }& =\log \left(w^{\ast }/w_{\mathrm{a}}\right),t_{\mathrm{h}}^{\ast }=\log \left(h^{\ast }/h_{\mathrm{a}}\right)\end{array}$$

1 * 1卷积数目时36，即输出是36d的，因为1个点有9个Anchor，每个点有4个值需要预测。所以一共有4 * k = 4 * 9 = 36个coordinates。

Proposal Layer

Proposal Layer负责综合所有变换量和positive anchors，计算出精准的proposal，送入后续RoI Pooling Layer。
这步总可以看做是RPN网络最后综合输出，回到原论文，边框检测的最终损失为：

$$\lambda \frac{1}{N_{reg}}\sum _i{p}_i^{\ast }{L}_{reg}\left(t_i,t_i^{\ast }\right)$$

其中，$p_i^{\ast }$表示是否是正负样本的Anchor

而在实际实现过程中：

Proposal Layer forward（caffe layer的前传函数）按照以下顺序依次处理：
生成anchors，利用[公式]对所有的anchors做bbox regression回归（这里的anchors生成和训练时完全一致）
按照输入的positive softmax scores由大到小排序anchors，提取前pre_nms_topN(e.g. 6000)个anchors，即提取修正位置后的positive anchors
限定超出图像边界的positive anchors为图像边界，防止后续roi pooling时proposal超出图像边界（见文章底部QA部分图21）
剔除尺寸非常小的positive anchors
对剩余的positive anchors进行NMS（nonmaximum suppression）
Proposal Layer有3个输入：positive和negative anchors分类器结果rpn_cls_prob_reshape，对应的bbox reg的(e.g. 300)结果作为proposal输出
之后输出proposal=[x1, y1, x2, y2]，注意，由于在第三步中将anchors映射回原图判断是否超出边界，所以这里输出的proposal是对应MxN输入图像尺度的，这点在后续网络中有用。另外我认为，严格意义上的检测应该到此就结束了，后续部分应该属于识别了。

解释im_info。对于一副任意大小PxQ图像，传入Faster RCNN前首先reshape到固定MxN，im_info=[M, N, scale_factor]则保存了此次缩放的所有信息。然后经过Conv Layers，经过4次pooling变为WxH=(M/16)x(N/16)大小，其中feature_stride=16则保存了该信息，用于计算anchor偏移量。

ROI、Classification、Bounding box regression

经过RPN得到proposal，然后经过ROI、Classification、Bounding box regression，原理的Fast R-CNN也差不多，不在赘述。
最终Faster R-CNN的损失如下:
$$\begin{array}{c}L\left(\left\{p_i\right\},\left\{t_i\right\}\right)=\frac{1}{N_{cls}}{\sum }_i{L}_{cls}\left(p_i,p_i^{\ast }\right)+\lambda \frac{1}{N_{reg}}{\sum }_i{p}_i^{\ast }{L}_{reg}\left(t_i,t_i^{\ast }\right)\end{array}$$

四、实验结果

五、结论与思考

作者结论

总结

主要参考知乎大佬白裳的文章，从代码角度解释Faster R-CNN。所以这篇笔记原论文内容比较少。R-CNN系列还剩Mask R-CNN

思考

参考

一文读懂Faster RCNN
Faster RCNN 学习笔记