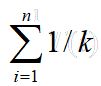分而治之——分治算法下快排和二分归并排序
算法一直是程序员必备的东西,了解算法在将来会对你求职和编程有很大帮助。
当然算法很难,它综合了数学、数据结构等一些知识。尤其是算法设计,为了设计出更有效,更节约时间的算法,必定要做大量演算。算法很难,所以面试会通过算法来刷人(无论你是研究生面试,还是工作面试)
算法为什么这么重要,因为算法是程序的灵魂,是编程的工具。这么说吧,你在玩游戏的时候,你希望你的打斗场面是一帧一帧的跟ppt那样播放吗?你希望在加载场景的时候用5分钟都不一定加载出来吗?你希望你的游戏运行时卡的让人受不了吗?算法就是在解决这个问题,我们需要一个时间复杂度小的算法来运行我们编写的程序。所以算法很重要,学习一些算法,可以帮助你优化你的程序。
大学时代学的算法主要是分为5大类:分治算法、动态规划算法(DP算法)、贪心算法、回溯算法(DFS算法)、分支限界算法(BFS)。本篇主要是介绍下分治算法,然后我们通过快排和二分归并排序来了解下分治算法。
1、对分治算法的认识
说到分治算法,首先得提到递归。因为分治的理念就是依靠着递归。
什么是递归?
对于某一函数f(x),其定义域是集合A,那么若对于A集合中的某一个值X0,其函数值f(x0)由f(f(x0))决定,那么就称f(x)为递归函数
哇!好抽象!这个我是在百度百科上看到的。
实际上递归是不断的调用自己,f(x)=f(f(x))决定,这个和后面提到的迭代是有着相反的意思。迭代是将上一部迭代出来的结果用到下一步开始迭代的条件,逐步迭代,直到满足条件为止;而递归就是,不断调用自己,直到遇到边界找到解,把解以此输送上面的递归步骤。
来,我们看个例子
public static void main(String[] args) {
recur();
}
private static void recur() {
// TODO Auto-generated method stub
recur();
}
recur()里面就是不断重复的调用自己,这就是递归。当然这种递归是无意义的,因为他没有递归出口和递归逻辑
其他的也就不多做介绍了,因为分治算法就是通过递归实现的,然而递归又在编程中占据了很重要的部分,所以我们通过例子再详细的接触下递归吧
现在我们回来看分治算法
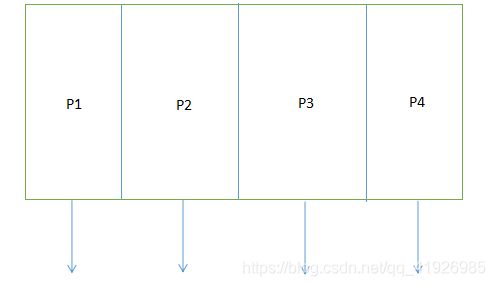
分治算法,即分而治之,其基本思想是将一个规模为N的问题分解为K个规模较小的子问题,这些子问题相互独立且与原问题性质相同。求出子问题的解,就可得到原问题的解。
分治策略:
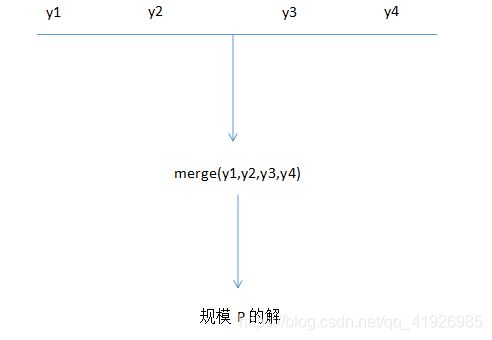
将原始问题划分或者归结为规模较小的子问题,然后通过递归来求解这些个子问题。然而如果划分出来的子问题可以很方便的求解了。那么我们将直接求解,然后将子问题的解综合得到原问题的解
什么是子问题
子问题就是原问题分出来的规模小的重复问题
分治算法模型:
divide-and-conquer§
{
if(|P|<=n0) adhoc§;
divide P into smaller subinstances P1,P2,…,Pk;
for(i=1,i<=k,i++)
yi=divide-and-conquer(Pi);
return merge(y1,…,yk);
}
我们再用伪码表示:
divide_and_conquer§
{
if |P|<=n0 then adhoc§
else
for i <- 1 to k
yi=divide_and_conquer§
return merge(yi)
}
分治算法注意事项:
1、子问题与原始问题性质完全一样(递归求解的基础)
2、子问题之间可彼此独立求解
3、递归停止时子问题可直接求解
######分治算法特点:
1、将原问题归约为规模小的子问题,其中子问题与原问题具有相同的性质
2、子问题规模足够小时可直接求解
3、算法可以递归也可以迭代实现
4、算法分析得出时间复杂度
说了这么多,也许你明白了分治算法的内容;也许你还是云里雾里。接下来我们看几个例子来感受下分治算法。
2、一种最有效的排序算法——快速排序算法
什么是快速排序?
正如其名,快速排序是一个特别能提高性能的排序算法。
快速排序是对冒泡排序的一种改进。
通过一趟排序将要排序的数据分割成独立的两部分,其中一部分的所有数据都比另外一部分的所有数据都要小,然后再按此方法对这两部分数据分别进行快速排序,整个排序过程可以递归进行,以此达到整个数据变成有序序列。
快速排序算法
快速排序也有很多算法,而且快速排序讲究的是划分,通过划分来对部分进行排序,最终达到想要的结果。然而划分又有很多种:单向划分、双向划分等
这里我们用一种双向划分来介绍快速排序。
1、在数组中定义一个基准数
2、在数组中从右往左寻找比基准数小的数,然后从左往右寻找比基准数大的数,两者进行交换。直到从右往左寻找的下标和从左往右寻找的下标重合为止
3、然后将最后寻找的比基准数小的数与基准数进行交换,这样使得基准数左边的数比基准数小,基准数右边的数比基准数大
4、将基准数为划分,划分出左右两个子问题,然后分别对子问题再进行排序
快速排序的实例
我们用5,8,1,3,6,2,4,7进行排序
这里我们用temp记录基准数(一般为首元素),left记录从左往右遍历的数组下标,right记录从右往左遍历的数组下标
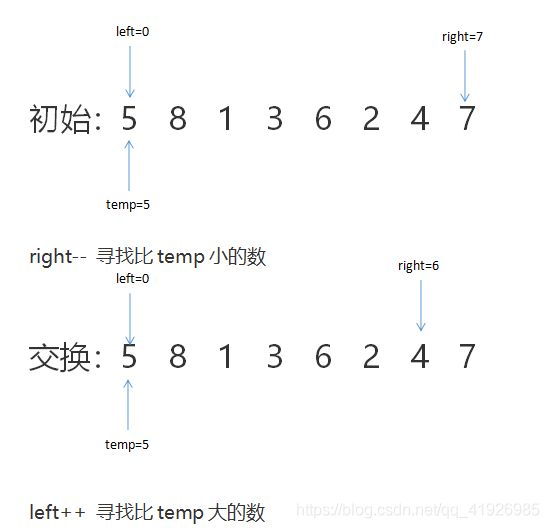







当然这是指针指着首尾元素交换的。当然left也可以从a[1]开始,当然如果是这样,那么当right
我们来分析下,在left为0时的这种情况怎么用递归写代码
首先需要三个变量,一个存数,两个记下标。对于right,初值肯定是n-1,因为重合便不再循环,那么right>left才能进入循环,而且还要a[right]>=temp(要从右往左找到比temp小的元素,才能right- -。进而逐步遍历找到目标位置)。而对于left则是left初值为0,循环条件right>left且a[left]<=temp。而对于递归根据上面的划分就是(数组a,0,right-1)和(数组a,right+1,n-1)。我们可以根据这些来写代码
快速排序伪码
这里置初值p=0,r=n,然后调用该算法
QuickSort(A,start,end)
输入:数组A[start…end]
输出:排好序的数组A
low<-start
high<-end
temp<-A[start]
while high>low do
{
repeat high<-high-1
until(A[high]
repeat low<-low+1
until(A[low]>temp||high
if high>low
then A[low]<->A[high]
}
A[start]<->A[high]
if low>start
then QuickSort(A,start,low-1)
if high then QuickSort(A,high+1,end)
快速排序代码
public static void main(String[] args) {
int a[]=new int[10];
Random random=new Random();
for(int i=0;i<10;i++)
a[i]=random.nextInt(11); //随机生成10个0到10的数字
System.out.println("生成的结果是:"+Arrays.toString(a));
QuickSort(a, 0, a.length-1);
System.out.println("排序的结果是:"+Arrays.toString(a));
}
//快速排序
public static void QuickSort(int a[],int start,int end) {
int low=start;
int high=end;
while(high>low) {
//从右往左遍历,寻找比首元素小的值
while(a[start]<=a[high]&&high>low) {
high--;
}
//从左往右遍历,寻找比首元素大的值
while(a[start]>=a[low]&&high>low) {
low++;
}
if(high>low) {
int temp;
temp=a[high];
a[high]=a[low];
a[low]=temp;
}
}
//将a[high]与首元素进行交换,此时这个首元素左边的全是比它小的,右边的全是比它大的
int temp;
temp=a[high];
a[high]=a[start];
a[start]=temp;
//递归
if(low>start)
QuickSort(a, start, low-1);
if(high<end)
QuickSort(a, high+1, end);
}
当然也可以让left=1进行编写代码。我找到了个比较规范的代码,可以看一下
先上伪码:


代码:
public static void main(String[] args) {
int a[]=new int[10];
Random random=new Random();
for(int i=0;i<10;i++)
a[i]=random.nextInt(11); //随机生成10个0到10的数字
System.out.println("生成的结果是:"+Arrays.toString(a));
Quicksort(a, 0, a.length-1);
System.out.println("排序的结果是:"+Arrays.toString(a));
}
//快速排序
public static int Partition(int a[],int start,int end) {
int temp=a[start];
int left=start+1;
int right=end;
int flag;
while(left<=right) {
while(left<=right&&a[left]<=temp)
left++;
while(left<=right&&a[right]>temp)
right--;
if(left<right) {
flag=a[left];
a[left]=a[right];
a[right]=flag;
}
}
flag=a[right];
a[right]=a[start];
a[start]=flag;
return right;
}
public static void Quicksort(int a[],int p,int q) {
if(p<q) {
int r=Partition(a, p, q);
Quicksort(a, p, r-1);
Quicksort(a, r+1, q);
}
}
快速排序分析
大家先想想正序和逆序。在这两种情况下,快速排序是如何进行的。是不是应用了这个排序,感觉越排越复杂。我们看
1 2 3 4 5 6
这几个数中,right找呀找,找到了left的位置。然后划分就成了1和2 3 4 5 6。1不用进行递推,因为left=start,所以不进入递归式里面。而后者的子问题是可以递推的。这样逐次划分,逐次递归。出来的还是1 2 3 4 5 6。而且逆序6 5 4 3 2 1也是这样的,最后变成了1 2 3 4 5 6。
这样的就是最坏时间复杂度,划分的子问题规模个数比例失调。上面的不就是1:n-1嘛。那么怎么求这个最坏时间复杂度?
我们在分析分治算法的时间复杂度,是要列出它的递归式,并求出这个递归式的通项公式。然后转化出时间复杂度
快速排序的最坏时间复杂度啊,递归分别是T(0)和T(n-1)。而且遍历,你看right到left(到了left是不是就不再循环遍历,而是直接跳出循环了),因此共遍历left-right+1次,因此就是n-0+1,即n-1次循环。
ok,想清楚后。我们写关系式
T(n)=T(n-1)+n-1
T(1)=0
怎么求这个数列的通项公式啊?
我们可以用迭代法求,也可以用高中学的累和累积法求。或者你也可以用下一篇将提到主定理和递归树来求。好,我们用累和法求

T(n)=n(n-1)/2因此求得时间复杂度是O(n^2),如果以上求解如果有不懂的,可以在底下评论。因为这种分析过程在算法分析里面很常见。
快速排序最重要的是划分,然而划分比例有问题,比例失调才使得时间复杂度变大
那么什么情况下是最好情况?
我们能想到,肯定是以中间进行划分。对,当每一轮排序结果是以中间为划分,才是最好情况。来,我们求一下在此时的时间复杂度。首先递归肯定是两个T(n/2)。遍历还是n-1
我们列出这个式子:
T(n)=2T(n/2)+n-1
T(1)=0
用迭代法解出:
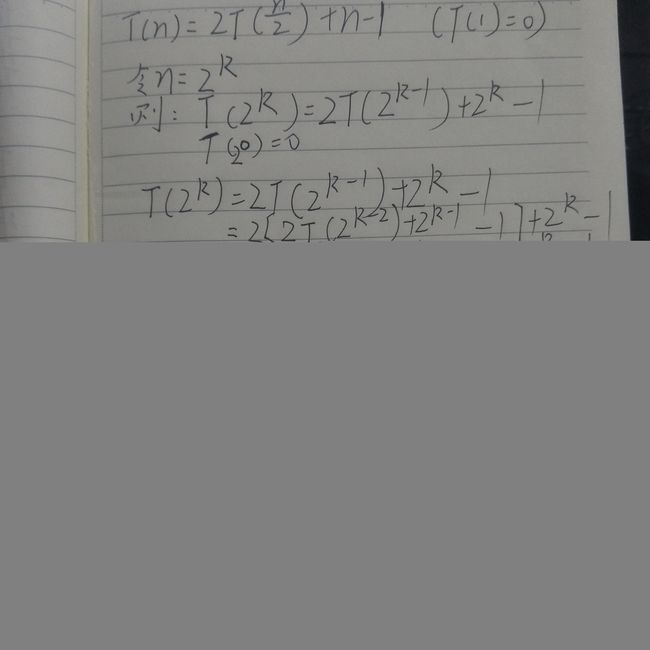
得到T(n)=n*logn-n+1,因此我们能得到最好时间复杂度是O(nlogn)
那么我们可以以此来优化快速排序
让划分的值在中间就可以了。就可以达到一种O(nlogn)的量
我们可以考虑用三点中值法
令mid=(left+right)/2
就是在a[left]、a[right]、a[mid]之间寻求一个中间值做基准
比较三个大小,选取中间的那个值作为基准数
这个很简单,不多说了。直接上代码
public static void main(String[] args) {
int a[]=new int[10];
Random random=new Random();
for(int i=0;i<10;i++)
a[i]=random.nextInt(11); //随机生成10个0到10的数字
System.out.println("生成的结果是:"+Arrays.toString(a));
QuickSort(a, 0, a.length-1);
System.out.println("排序的结果是:"+Arrays.toString(a));
}
//优化快速排序
public static void QuickSort(int a[],int start,int end) {
int mid=(start+end)>>>1; //优化,在start,end,mid之间选择一个中间值作为基准数
int midvalue; //中间值的下标
if(a[start]<=a[mid]&&a[start]>=a[end]||a[start]>=a[mid]&&a[start]<=a[end])
midvalue=start;
else if(a[end]<=a[mid]&&a[end]>=a[start]||a[end]>=a[mid]&&a[end]<=a[start])
midvalue=end;
else midvalue=mid;
int flag; //交换标记:拿到中间值和首元素交换下。这里只产生了O(1)的时间复杂度
flag=a[midvalue];
a[midvalue]=a[start];
a[start]=flag;
int pivot=a[start];
int low=start;
int high=end;
while(high>low) {
//从右往左遍历,寻找比首元素小的值
while(pivot<=a[high]&&high>low) {
high--;
}
//从左往右遍历,寻找比首元素大的值
while(pivot>=a[low]&&high>low) {
low++;
}
if(high>low) {
int temp;
temp=a[high];
a[high]=a[low];
a[low]=temp;
}
}
int temp;
temp=a[high];
a[high]=a[start];
a[start]=temp;
//递归
if(low>start)
QuickSort(a, start, low-1);
if(high<end)
QuickSort(a, high+1, end);
}
ok,我们就这样把算法的量降到nlogn。当然我们可以再优化
经过测试与发现啊,当要排序的数的个数比较少的时候,发现插入排序的效率比快排要高,也就是说如果你的数组长度比较小,一个插入排序就足够了。如果是庞大的数据快排的效率要高。经一些人实测在数据长度为8个以内时调用插入排序为最佳,大于8个可以选择调用快速排序。代码改写工作很简单这里就不展示了(一个if-else就可以干掉的)
当然网上也有一下把快速排序算法降到O(logn)的量,这个感兴趣的伙伴,可以自己去搜一搜吧。这里不做阐述了
下面我们来研究快速排序算法的平均时间复杂度
这个快速排序的平均时间复杂度是O(nlogn)。这个证明。额,想看就看吧。不想看就跳过(毕竟这是我为数不多能证出来的)
(证明环节,不想看可以选择跳过)
首先我们先看一个求平均时间复杂度的公式A(n)
A(n)=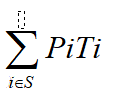
在某些情况下可以假定每个输入实例的概率相等
设S是规模为n的实例集,实例I属于S的概率是Pi,算法对实例i的执行的基本运算次数是Ti
说白了就是在假定每个输入实例的概率相等的情况下,平均时间复杂度就是将所有情况下代码执行次数累加起来,然后除以输入实例的总数量
大家应该可以清楚快速排序的输入实例就是数组,因此数组长度就是输入实例的总数量,即n
下面我们来考虑代码执行次数
我们来看看子问题递归和遍历找划分这两块内容(其余内容:如两数交换和判断都是O(1)的量的代码)


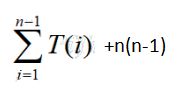

我们对这个式子用差消法来解
这里我们用不定积分来求解。
看这个面积第一个是1,第二个是1/2,第三个是1/3…第n个是1/n
将面积加起来。然后你能看到1/x的面积完全被顶上那个级数的面积覆盖,因此我们可以用1/x的面积算作下界。所以经过解完,就是下界ln n(那个符号是下界符号)
然后我们来算它的上界,用同样的方法
最后我们得出调和级数的界为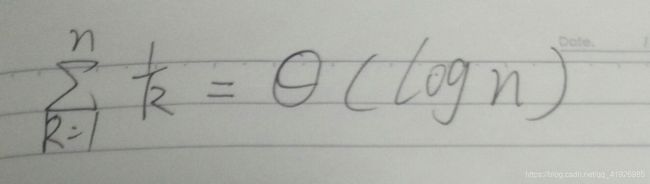
(如果上界和下界的值是一样的,那么可以用这个符号)
因此得出平均时间复杂度:
好,以上就是平均时间复杂度的解法
至于为什么说快速排序算法是效率比较高的。这个还是自己实践,自己感受吧。这里就不再测了
哦,对了。还有我们知道JAVA里面封装了一个方法Arrays.sort();
JAVA在内置的sort方法中做了很多的努力,包括分析比较排序性能,在数组较小的时候采用插入排序等排序方法提高效率。
而且可以很好的举出反例证明快速排序是不稳定算法。
这就是快速排序与分治算法的内容,快速排序通过遍历寻求划分,划分出子问题。然后递归子问题最后归结出最后的结果。分治算法就是通过分解出与原问题同性质的子问题,然后分析子问题,将解归结后得到原问题的解。这就是分治算法。
3、二分归并排序算法
什么是二分归并排序
这个和二分检索差不多,是建立在归并操作上的一种有效的排序算法,该算法是采用分治法的一个非常典型的应用。将已有序的子序列合并,得到完全有序的序列;即先使每个子序列有序,再使子序列段间有序。若将两个有序表合并成一个有序表,称为二路归并。归并排序是一种稳定的排序方法。
二分归并排序算法
1、将数据通过递归逐步一分为二,直至将数据划成1个
2、然后将分好的数据逐步排序
3、陆续归并被排好序的两个字数组,每归并一次,数组规模扩大一倍,知道原始数组
二分归并排序实例
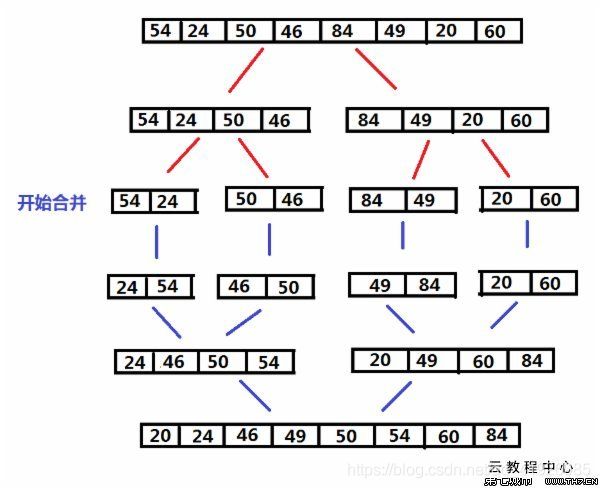
我们来分析下,首先我们需要两个同长度的数组,归并的时候我们拿24 54 46 50这一组分析。我们比较是拿24和46比较,24<46,然后将24加到另一个数组里。46<54,然后将46加进去。然后50<54,然后将50加进去,最后将54加进去。最后结果是24 46 50 54。我们再分析发现出如果12 47 89 102 45 53 62。首先一分为二,也许你会想一分为二怎么做到的?这个在递归已经分好了(mid=(left+right)/2)。你猜的没错,mid这个既可以分开数组递归一分为二,也可以传到排序方法里面作归结用。
我们看计算mid,然后将数据一分为二,递归传入(两个数组(一个是原数组,一个是备用数组),start,mid)以及另外一半的(两个数组,mid+1,end)。将分好的东西再传入排序算法里面(两数组,start,mid(这个就是我刚才要用来进行排序用),end)。然后来到排序算法,我们要比较肯定不能把已经排好的数据再比较一次吧,大家想一想参考上面那些数据是怎么比较的,是不是第一个和一半以后的那一个比较的?是不是第一个和一半之前的数据是排好序的。因此需要i,j i从0开始到i<=mid,j从mid+1开始到j<=end。比较出来干嘛呢?按升序排序来看,谁小就进入另一个备好的数组里面。大家再看上一个数据 12 47 89 102 45 53 62。化为一半就是12 47 89 102和45 53 62,大家可以自己分析分析比较,想一想进入备用的数据是什么。是不是12 45 47 53 62 89 102。没错右边已经空了,就将左边的排好的直接放进去就行了(这个过程的代码分析就放给大家,不会一会看代码吧)。伪码先展示出来:

代码再展示出来:
public static void main(String[] args) {
int a[]=new int[10];
Random random=new Random();
for(int i=0;i<10;i++)
a[i]=random.nextInt(11); //随机生成10个0到10的数字
System.out.println("生成的结果是:"+Arrays.toString(a));
Sort(a, 0, a.length-1);
System.out.println("排序的结果是:"+Arrays.toString(a));
}
public static void Sort(int source[],int start,int end) {
int temp[]=new int[source.length];
MergeSort(source, temp, start, end);
}
public static void MergeSort(int source[],int temp[],int start,int end) {
if(start<end) {
int mid=(start+end)>>>1; //这里用位运算替换除法,更能提高运行速度
MergeSort(source,temp, start, mid);
MergeSort(source, temp, mid+1, end);
Merge(source, temp, start, mid, end);
}
}
//二分归并排序
public static void Merge(int source[],int temp[],int start,int mid,int end) {
int i=start,j=mid+1,k=start;
while(i<=mid&&j<=end) {
if(source[i]<=source[j]) {
temp[k++]=source[i++];
}
else {
temp[k++]=source[j++];
}
}
while(i!=mid+1) {
temp[k++]=source[i++];
}
while(j!=end+1) {
temp[k++]=source[j++];
}
//归结
for(i=start;i<=end;i++) {
source[i]=temp[i];
}
}
二分归并排序算法分析
和快排一样。这个不存在什么好坏之分。算法分析都一样,因为递归都是2T(n/2),循环遍历就是那个归结是n个。即使数据循环我觉得也得遍历n次
因此可列出公式T(n)=2T(n/2)+O(n)。这个的解法和快排差不多,这里就不再解了。
直接放出最后答案,最好时间复杂度和最坏时间复杂度和平均时间复杂度都是O(nlogn)。这个就放给大家了。
二分归并排序是一种稳定排序
算法这个东西,很复杂很庞大。这些我上面陈述的都仅仅是基础。放到打acm那些人里面都能笑死。所以这些基础要了解
编程——我们不应该仅仅局限于中国编写的教材,外国的东西也许更有见解也说不定。加油吧!
我们来分析下,在left为0时的这种情况怎么用递归写代码
首先需要三个变量,一个存数,两个记下标。对于right,初值肯定是n-1,因为重合便不再循环,那么right>left才能进入循环,而且还要a[right]>=temp(要从右往左找到比temp小的元素,才能right- -。进而逐步遍历找到目标位置)。而对于left则是left初值为0,循环条件right>left且a[left]<=temp。而对于递归根据上面的划分就是(数组a,0,right-1)和(数组a,right+1,n-1)。我们可以根据这些来写代码
快速排序伪码
这里置初值p=0,r=n,然后调用该算法 repeat low<-low+1 if high>low A[start]<->A[high] if low>start 当然也可以让left=1进行编写代码。我找到了个比较规范的代码,可以看一下 大家先想想正序和逆序。在这两种情况下,快速排序是如何进行的。是不是应用了这个排序,感觉越排越复杂。我们看 快速排序最重要的是划分,然而划分比例有问题,比例失调才使得时间复杂度变大 那么我们可以以此来优化快速排序 ok,我们就这样把算法的量降到nlogn。当然我们可以再优化 下面我们来研究快速排序算法的平均时间复杂度 (证明环节,不想看可以选择跳过) 说白了就是在假定每个输入实例的概率相等的情况下,平均时间复杂度就是将所有情况下代码执行次数累加起来,然后除以输入实例的总数量 大家应该可以清楚快速排序的输入实例就是数组,因此数组长度就是输入实例的总数量,即n 下面我们来考虑代码执行次数 我们来看看子问题递归和遍历找划分这两块内容(其余内容:如两数交换和判断都是O(1)的量的代码) 这里我们用不定积分来求解。 然后我们来算它的上界,用同样的方法 最后我们得出调和级数的界为 因此得出平均时间复杂度: 好,以上就是平均时间复杂度的解法 至于为什么说快速排序算法是效率比较高的。这个还是自己实践,自己感受吧。这里就不再测了 哦,对了。还有我们知道JAVA里面封装了一个方法Arrays.sort(); 而且可以很好的举出反例证明快速排序是不稳定算法。 这就是快速排序与分治算法的内容,快速排序通过遍历寻求划分,划分出子问题。然后递归子问题最后归结出最后的结果。分治算法就是通过分解出与原问题同性质的子问题,然后分析子问题,将解归结后得到原问题的解。这就是分治算法。 这个和二分检索差不多,是建立在归并操作上的一种有效的排序算法,该算法是采用分治法的一个非常典型的应用。将已有序的子序列合并,得到完全有序的序列;即先使每个子序列有序,再使子序列段间有序。若将两个有序表合并成一个有序表,称为二路归并。归并排序是一种稳定的排序方法。 1、将数据通过递归逐步一分为二,直至将数据划成1个 和快排一样。这个不存在什么好坏之分。算法分析都一样,因为递归都是2T(n/2),循环遍历就是那个归结是n个。即使数据循环我觉得也得遍历n次 二分归并排序是一种稳定排序
QuickSort(A,start,end)
输入:数组A[start…end]
输出:排好序的数组A
low<-start
high<-end
temp<-A[start]
while high>low do
{
repeat high<-high-1
until(A[high]
until(A[low]>temp||high
then A[low]<->A[high]
}
then QuickSort(A,start,low-1)
if high快速排序代码
public static void main(String[] args) {
int a[]=new int[10];
Random random=new Random();
for(int i=0;i<10;i++)
a[i]=random.nextInt(11); //随机生成10个0到10的数字
System.out.println("生成的结果是:"+Arrays.toString(a));
QuickSort(a, 0, a.length-1);
System.out.println("排序的结果是:"+Arrays.toString(a));
}
//快速排序
public static void QuickSort(int a[],int start,int end) {
int low=start;
int high=end;
while(high>low) {
//从右往左遍历,寻找比首元素小的值
while(a[start]<=a[high]&&high>low) {
high--;
}
//从左往右遍历,寻找比首元素大的值
while(a[start]>=a[low]&&high>low) {
low++;
}
if(high>low) {
int temp;
temp=a[high];
a[high]=a[low];
a[low]=temp;
}
}
//将a[high]与首元素进行交换,此时这个首元素左边的全是比它小的,右边的全是比它大的
int temp;
temp=a[high];
a[high]=a[start];
a[start]=temp;
//递归
if(low>start)
QuickSort(a, start, low-1);
if(high<end)
QuickSort(a, high+1, end);
}
先上伪码:


代码:public static void main(String[] args) {
int a[]=new int[10];
Random random=new Random();
for(int i=0;i<10;i++)
a[i]=random.nextInt(11); //随机生成10个0到10的数字
System.out.println("生成的结果是:"+Arrays.toString(a));
Quicksort(a, 0, a.length-1);
System.out.println("排序的结果是:"+Arrays.toString(a));
}
//快速排序
public static int Partition(int a[],int start,int end) {
int temp=a[start];
int left=start+1;
int right=end;
int flag;
while(left<=right) {
while(left<=right&&a[left]<=temp)
left++;
while(left<=right&&a[right]>temp)
right--;
if(left<right) {
flag=a[left];
a[left]=a[right];
a[right]=flag;
}
}
flag=a[right];
a[right]=a[start];
a[start]=flag;
return right;
}
public static void Quicksort(int a[],int p,int q) {
if(p<q) {
int r=Partition(a, p, q);
Quicksort(a, p, r-1);
Quicksort(a, r+1, q);
}
}
快速排序分析
1 2 3 4 5 6
这几个数中,right找呀找,找到了left的位置。然后划分就成了1和2 3 4 5 6。1不用进行递推,因为left=start,所以不进入递归式里面。而后者的子问题是可以递推的。这样逐次划分,逐次递归。出来的还是1 2 3 4 5 6。而且逆序6 5 4 3 2 1也是这样的,最后变成了1 2 3 4 5 6。
这样的就是最坏时间复杂度,划分的子问题规模个数比例失调。上面的不就是1:n-1嘛。那么怎么求这个最坏时间复杂度?
我们在分析分治算法的时间复杂度,是要列出它的递归式,并求出这个递归式的通项公式。然后转化出时间复杂度
快速排序的最坏时间复杂度啊,递归分别是T(0)和T(n-1)。而且遍历,你看right到left(到了left是不是就不再循环遍历,而是直接跳出循环了),因此共遍历left-right+1次,因此就是n-0+1,即n-1次循环。
ok,想清楚后。我们写关系式
T(n)=T(n-1)+n-1
T(1)=0
怎么求这个数列的通项公式啊?
我们可以用迭代法求,也可以用高中学的累和累积法求。或者你也可以用下一篇将提到主定理和递归树来求。好,我们用累和法求

T(n)=n(n-1)/2因此求得时间复杂度是O(n^2),如果以上求解如果有不懂的,可以在底下评论。因为这种分析过程在算法分析里面很常见。
那么什么情况下是最好情况?
我们能想到,肯定是以中间进行划分。对,当每一轮排序结果是以中间为划分,才是最好情况。来,我们求一下在此时的时间复杂度。首先递归肯定是两个T(n/2)。遍历还是n-1
我们列出这个式子:
T(n)=2T(n/2)+n-1
T(1)=0
用迭代法解出:
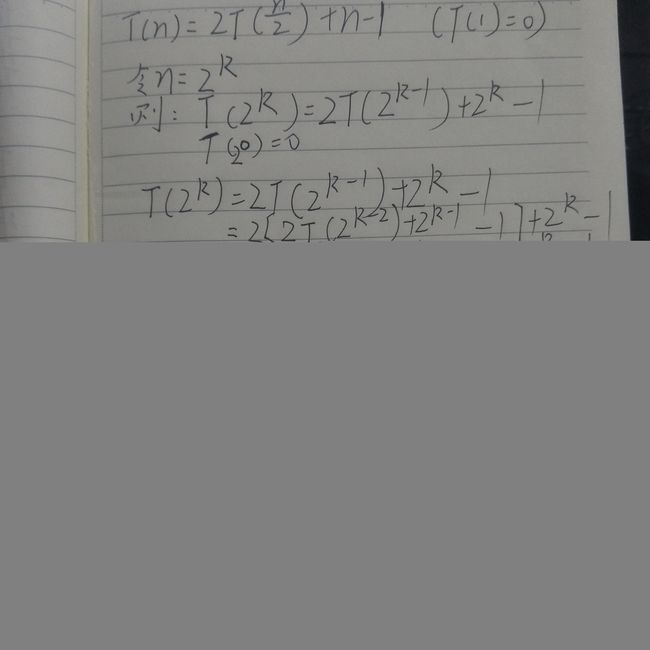
得到T(n)=n*logn-n+1,因此我们能得到最好时间复杂度是O(nlogn)
让划分的值在中间就可以了。就可以达到一种O(nlogn)的量
我们可以考虑用三点中值法
令mid=(left+right)/2
就是在a[left]、a[right]、a[mid]之间寻求一个中间值做基准
比较三个大小,选取中间的那个值作为基准数
这个很简单,不多说了。直接上代码public static void main(String[] args) {
int a[]=new int[10];
Random random=new Random();
for(int i=0;i<10;i++)
a[i]=random.nextInt(11); //随机生成10个0到10的数字
System.out.println("生成的结果是:"+Arrays.toString(a));
QuickSort(a, 0, a.length-1);
System.out.println("排序的结果是:"+Arrays.toString(a));
}
//优化快速排序
public static void QuickSort(int a[],int start,int end) {
int mid=(start+end)>>>1; //优化,在start,end,mid之间选择一个中间值作为基准数
int midvalue; //中间值的下标
if(a[start]<=a[mid]&&a[start]>=a[end]||a[start]>=a[mid]&&a[start]<=a[end])
midvalue=start;
else if(a[end]<=a[mid]&&a[end]>=a[start]||a[end]>=a[mid]&&a[end]<=a[start])
midvalue=end;
else midvalue=mid;
int flag; //交换标记:拿到中间值和首元素交换下。这里只产生了O(1)的时间复杂度
flag=a[midvalue];
a[midvalue]=a[start];
a[start]=flag;
int pivot=a[start];
int low=start;
int high=end;
while(high>low) {
//从右往左遍历,寻找比首元素小的值
while(pivot<=a[high]&&high>low) {
high--;
}
//从左往右遍历,寻找比首元素大的值
while(pivot>=a[low]&&high>low) {
low++;
}
if(high>low) {
int temp;
temp=a[high];
a[high]=a[low];
a[low]=temp;
}
}
int temp;
temp=a[high];
a[high]=a[start];
a[start]=temp;
//递归
if(low>start)
QuickSort(a, start, low-1);
if(high<end)
QuickSort(a, high+1, end);
}
经过测试与发现啊,当要排序的数的个数比较少的时候,发现插入排序的效率比快排要高,也就是说如果你的数组长度比较小,一个插入排序就足够了。如果是庞大的数据快排的效率要高。经一些人实测在数据长度为8个以内时调用插入排序为最佳,大于8个可以选择调用快速排序。代码改写工作很简单这里就不展示了(一个if-else就可以干掉的)
当然网上也有一下把快速排序算法降到O(logn)的量,这个感兴趣的伙伴,可以自己去搜一搜吧。这里不做阐述了
这个快速排序的平均时间复杂度是O(nlogn)。这个证明。额,想看就看吧。不想看就跳过(毕竟这是我为数不多能证出来的)
首先我们先看一个求平均时间复杂度的公式A(n)
A(n)=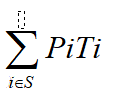
在某些情况下可以假定每个输入实例的概率相等
设S是规模为n的实例集,实例I属于S的概率是Pi,算法对实例i的执行的基本运算次数是Ti

![]()
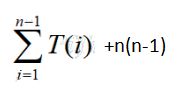

我们对这个式子用差消法来解
看这个面积第一个是1,第二个是1/2,第三个是1/3…第n个是1/n
将面积加起来。然后你能看到1/x的面积完全被顶上那个级数的面积覆盖,因此我们可以用1/x的面积算作下界。所以经过解完,就是下界ln n(那个符号是下界符号)
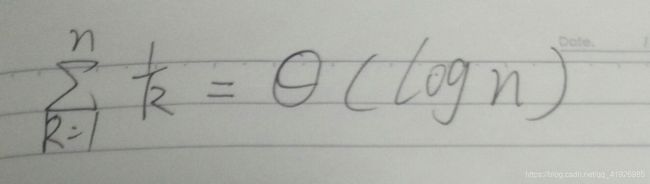
(如果上界和下界的值是一样的,那么可以用这个符号)
JAVA在内置的sort方法中做了很多的努力,包括分析比较排序性能,在数组较小的时候采用插入排序等排序方法提高效率。3、二分归并排序算法
什么是二分归并排序
二分归并排序算法
2、然后将分好的数据逐步排序
3、陆续归并被排好序的两个字数组,每归并一次,数组规模扩大一倍,知道原始数组二分归并排序实例

我们来分析下,首先我们需要两个同长度的数组,归并的时候我们拿24 54 46 50这一组分析。我们比较是拿24和46比较,24<46,然后将24加到另一个数组里。46<54,然后将46加进去。然后50<54,然后将50加进去,最后将54加进去。最后结果是24 46 50 54。我们再分析发现出如果12 47 89 102 45 53 62。首先一分为二,也许你会想一分为二怎么做到的?这个在递归已经分好了(mid=(left+right)/2)。你猜的没错,mid这个既可以分开数组递归一分为二,也可以传到排序方法里面作归结用。
我们看计算mid,然后将数据一分为二,递归传入(两个数组(一个是原数组,一个是备用数组),start,mid)以及另外一半的(两个数组,mid+1,end)。将分好的东西再传入排序算法里面(两数组,start,mid(这个就是我刚才要用来进行排序用),end)。然后来到排序算法,我们要比较肯定不能把已经排好的数据再比较一次吧,大家想一想参考上面那些数据是怎么比较的,是不是第一个和一半以后的那一个比较的?是不是第一个和一半之前的数据是排好序的。因此需要i,j i从0开始到i<=mid,j从mid+1开始到j<=end。比较出来干嘛呢?按升序排序来看,谁小就进入另一个备好的数组里面。大家再看上一个数据 12 47 89 102 45 53 62。化为一半就是12 47 89 102和45 53 62,大家可以自己分析分析比较,想一想进入备用的数据是什么。是不是12 45 47 53 62 89 102。没错右边已经空了,就将左边的排好的直接放进去就行了(这个过程的代码分析就放给大家,不会一会看代码吧)。伪码先展示出来:

代码再展示出来:public static void main(String[] args) {
int a[]=new int[10];
Random random=new Random();
for(int i=0;i<10;i++)
a[i]=random.nextInt(11); //随机生成10个0到10的数字
System.out.println("生成的结果是:"+Arrays.toString(a));
Sort(a, 0, a.length-1);
System.out.println("排序的结果是:"+Arrays.toString(a));
}
public static void Sort(int source[],int start,int end) {
int temp[]=new int[source.length];
MergeSort(source, temp, start, end);
}
public static void MergeSort(int source[],int temp[],int start,int end) {
if(start<end) {
int mid=(start+end)>>>1; //这里用位运算替换除法,更能提高运行速度
MergeSort(source,temp, start, mid);
MergeSort(source, temp, mid+1, end);
Merge(source, temp, start, mid, end);
}
}
//二分归并排序
public static void Merge(int source[],int temp[],int start,int mid,int end) {
int i=start,j=mid+1,k=start;
while(i<=mid&&j<=end) {
if(source[i]<=source[j]) {
temp[k++]=source[i++];
}
else {
temp[k++]=source[j++];
}
}
while(i!=mid+1) {
temp[k++]=source[i++];
}
while(j!=end+1) {
temp[k++]=source[j++];
}
//归结
for(i=start;i<=end;i++) {
source[i]=temp[i];
}
}
二分归并排序算法分析
因此可列出公式T(n)=2T(n/2)+O(n)。这个的解法和快排差不多,这里就不再解了。
直接放出最后答案,最好时间复杂度和最坏时间复杂度和平均时间复杂度都是O(nlogn)。这个就放给大家了。算法这个东西,很复杂很庞大。这些我上面陈述的都仅仅是基础。放到打acm那些人里面都能笑死。所以这些基础要了解
编程——我们不应该仅仅局限于中国编写的教材,外国的东西也许更有见解也说不定。加油吧!