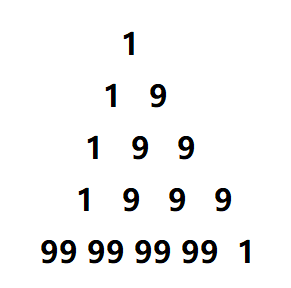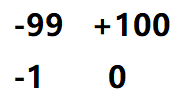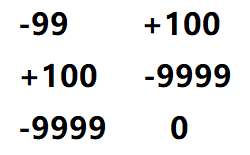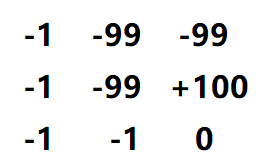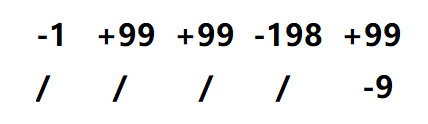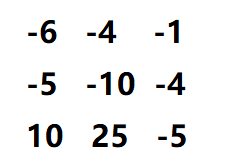【编程学习笔记】老子今天一定要学会动态规划！

从刚开始接触算法到现在，已经无数次听到动态规划这个算法了。

似乎每次看到一道不会做的算法题，旁边就会有大佬喊道“这不就典型的DP嘛”，然后三下五除二解决了。

于是，我无数次地想要功课这个神乎其神的算法，却每次在看到那令人头痛的公式之后就望而却步。

如今！作为一个已经接触算法四年的我！一定要学会动态规划！！！

 

一、基本思想

动态规划就是把一个大问题A，分解成小问题A1、A2、A3、A4.....，然后A1的输出为A2的输入，A2的输出为A3的输入...以此类推，使得一个复杂的问题变成多个简单的问题，并且最后一个小问题的解就是A的解

要做到这一点，就需要实现两件事情：

① 小问题如何划分？

比如从C市到D市的最优路径，如何分割成多个小问题？是走一座城？还是走一天？还是花多少钱？

② 小问题之间的关系是什么？

由于小问题是连续且前后关联的，所以必须要搞清楚，前一个小问题和后一个小问题如何通过一个函数关联起来。

 

二、 先来看一个题：

如下图，从“7”开始，只能向左下或右下走，求路径最大数字和

求解这个问题，我们抓住“怎么划分小问题”和“小问题间的关联”来思考

首先，对于某一层某个位置，我们要往下怎么走，这就是一个小问题，比如我们走到了1这个地方，那么接下来走7还是走4就是一个小问题。

其次，对于某一个选择，我们只需要加上选择所对应的（下一层的）那个数，就转换到了下一个小问题

所以小问题就是Maxsum(r,j)处的选择 其中r，j表示当前走到了r行j列的位置,Maxsum(r,j)表示这一步做出最好选择时能余下各层获得的最大数字和

小问题关联就是Maxsum(r+1,j) = Maxsum(r,j)+value(r+1,j) 或 Maxsum(r,j)+value(r+1,j+1)

而这个式子就叫做“状态转移方程”，在更复杂的问题中，这个方程会更加复杂，但是这是所有动态规划问题的核心。

 

三、递归解决

有了上面这个式子，我们就可以递归了！

可以看出，这就是一个简单的递归问题，类似于斐波那契数列。

当然，你看到这可能就瑟瑟发抖了....这种递归岂不是效率极低？没关系，我们按照传统办法对结果进行一个存储即可，即设置一个二维数组，填满-1，该函数return前在对应(r,j)的位置插入计算结果，在每次调用前，先找二维数组，如果不是-1就直接拿来用。

 

四、动态规划真的能解决问题吗？

这也是一直困扰我的问题，为什么动态规划能解决问题，比如下图：

会不会从左边一路走下去然后给出一个103的错误答案？（这就很像DFS，但是DFS是有回溯的，这种递归又是怎么回溯的呢）

我们再回到这里：

对于整个大问题，我们要解决的是MaxSum(1,1)，也就是从(1,1)开始该如何选择是最优的，直到问题达到max(5,j)为止（这就很像汉诺塔问题）。当我们启动MaxSum(1,1)之后，程序就会进入MaxSum(2,1)，然后MaxSum(3,1)和MaxSum(3,2）。也就是逐步地一层一层进行最优的查找，直到第五层只有能够直接比较两个数时（全部分解成了最小问题）回溯。我们发现，这种递归实际上就是DFS（或者说DFS就是一种简单的动态规划？）所以，就算左边的MaxSum(2,1)给出了一个看似很好地解103，也终究被MaxSum(2,2)执行完毕后给出的29替换掉。而对于每一层，这个过程都是类似的。

 

五、来看一道实战题理解上面所说的内容

(提示：骑士可能会在中途就死掉！)

我们首先考虑一个局部：

骑士现在在-99的位置（可怜地掉了99滴血），接着他要往右或者往下。

如果走+100，那么+100只有一种选择就是往下，而往下的返回值必然是0，所以+100的最优情况是+100

如果走-1,那么-1的最优情况是-1

那骑士当然要走+100啦。可是呢？这并不意味着骑士能空血冲进去，不然一上来就会死掉，所以，-99这里的最优情况仍然是-99，也就是说，只能减不能加

再看这种情况，两个+100处的最优情况都是-9899，所以-99的最优解只能是-9998，这也符合实际情况，仍然说明只能减不能加

进一步扩大一些：

我们已经提到，（1,1）的-99的最优情况是-99，那么(1,0)的-1向右的最优解就是-99，而向下的最优解是-2（显然），所以勇士在这里会向下走，掉3血，而不是向右走掉100血。我们可以看到，如果是路径最大值，答案应该是-1，而在本题中，答案是-4

如果是这种情况呢？

第一层有两个+99和一个-198抵消，也就是说，这里勇士自己不需要准备血。我们前面说了只能减不能加，(0,4)处会被写为90没毛病，然后-198处因为其右侧为正，不能加，故还是-198，其左两个+99分别为变为0，-99，因此-1处会是-1+0=-1,勇士需要准备2滴血即可。如果-198改为-199，则两个+99处分别为-1和98，勇士需要准备3滴血，如果-198处改为-197，则-1处不加，仍然是-1，勇士还是需要准备2滴血。只减不加依然成立！

接下来我们就要开始DP了。

首先，小问题肯定还是在（i,j）位置处，如何选择，具体实现在程序中就是(i，j)处到(m,n)处的最小消耗。

接下来是寻找状态转移方程，也就是小问题之间的关联。还是拿上图（1,1）的-99处和（2,2）的0处为例，如果这个点是最右下的点，也就是说i=M-1；j=N-1，则最优解就是这个格子的值。其它情况（比如-99处），如果向右且向右后j小于N，则该格子的最优解备选项之一就是该格子的值加上(i,j+1)的最优解，向下同理得到一个备选项，两者之间取更大的那一个作为更优解（勇士当然要选扣血少的路），这个更优解如果大于等于0，则向上报告当前格子里的值，更优解如果小于0，则向上报告当前格子里的值加上更优解对应的值。当然，最终骑士至少要准备1滴血，不能0血或者负血。

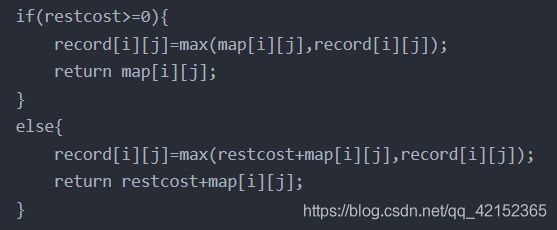
贴出代码（我在LeetCode上写的所以不是完整代码，重点看DP函数即可）：

class Solution {
public:
    int layer = 0;
    int width = 0;
    int** record;
#define INF 9999
    int DP(int i,int j,vector>& map){
        if(i==layer-1 && j==width-1){
            record[i][j]=map[i][j];
            return map[i][j];
        }
        else{
            int down=-INF,right=-INF;
            if(i+1-INF){down = record[i+1][j];}
                else{down = DP(i+1,j,map);}
            }
            if(j+1-INF){right = record[i][j+1];}
                else{right = DP(i,j+1,map);}
            }
            int restcost = max(down,right);
            if(restcost>=0){
                record[i][j]=max(map[i][j],record[i][j]);
                return map[i][j];
            }
            else{
                record[i][j]=max(restcost+map[i][j],record[i][j]);
                return restcost+map[i][j];
            }
        }
    }
    int calculateMinimumHP(vector>& dungeon) {
        layer = dungeon.size();
        width = dungeon[0].size();
        record = new int*[layer];
        for(int k=0;k

状态转移部分和小问题的解决都在这里：

该代码内存效率较高，但是时间效率一般，大家还可以进一步想一想减少时间消耗的办法。

如果还是不能理解，可以看下我本体样例输入的检测过程中输出的record（各位置最佳消耗记录）：

找到最优解前的输出：

最优解（最终）输出：

所以DP(1,1)的答案就是-6，也就是勇士需要7滴血

 

六、什么？上面的DP太low了？

没错，上面的动归只是个入门，如果要进一步学习DP，达到CCF甚至ACM的要求，就要开始分类学习各种进阶递归，这里提供一个网站，把前几个学会（后面觉得太难就算了），你的DP就可以实战运用了：

https://www.cnblogs.com/Archger/p/8451622.html