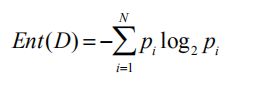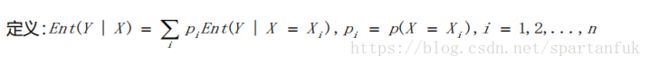python详细步骤计算信息增益
信息增益(gain):表示得知特征X的信息使得类Y的信息不确定性减少的程度。例如属性a的信息增益为:
信息增益就是等于某个属性的熵减去该属性的条件信息熵。熵的计算公式:
条件熵的计算公式:
#############################################################################
#自定义一份数据,分别计算信息熵,条件信息熵,从而计算信息增益;并打包成函数。
data1 = pd.DataFrame({'天气':['晴','晴','阴','雨','雨','雨','阴','晴','晴','雨','晴','阴','阴','雨'],
'温度':['高','高','高','低','低','低','低','低','低','低','低','低','高','低'],
'湿度':['高','低','高','高','高','低','低','高','低','高','低','高','低','高'],
'起风':[False,True,False,False,False,True,True,False,False,False,True,True,False,True],
'打球':['NO','NO','YES','YES','YES','NO','YES','NO','YES','YES','YES','YES','YES','NO']})
data1[['天气','温度','湿度','起风','打球']]#计算熵
prob1 = pd.value_counts(data1['打球']) / len(data1['打球'])
import numpy as np
sum(np.log2(prob1)*prob1*(-1))#计算条件信息熵
e1 = data1.groupby('天气').apply(lambda x:ent(x['打球']))
p1 = pd.value_counts(data1['天气']) / len(data1['天气'])
e2 = sum(e1*p1)
#计算信息增益
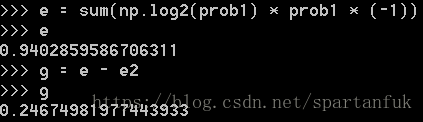
e = sum(np.log2(prob1) * prob1 * (-1)) #熵
e2 条件信息熵
g = e - e2 #信息增益
###############打包成函数
#定义计算熵的函数
def ent(data):
prob1 = pd.value_counts(data) / len(data)
return sum(np.log2(prob1) * prob1 * (-1))
#定义计算信息增益的函数
def gain(data,str1,str2):
e1 = data.groupby(str1).apply(lambda x:ent(x[str2]))
p1 = pd.value_counts(data[str1]) / len(data[str1])
e2 = sum(e1 * p1)
return ent(data[str2]) - e2
#测试
gain(data1,'天气','打球')