算法学习笔记——常用十个排序算法汇总
常用排序算法汇总
1、插入排序
简介:作为算法导论上的第一个排序算法,插入排序理解起来不难。其基本原理如图所示
排序机理:从左向右扫描,每遇到一个数字temp就将其从右向左,与位于temp-1的数进行大小比较,如果满足大小在两数之间,就执行插入,所谓的插入,本质是通过改变元素在数组中的位置,每比较一个数字,若不满足,则temp向左一位,temp-1的数字右移一位。
时间复杂度:O(n^2)
稳定性:稳是稳,就会慢了点
代码:
void insertion_sort (int arr[],int length)
{//插入排序
int i,j;
for(i=1;i<length;i++)
{
int temp=arr[i];
for(j=i;j>0&&arr[j-1]>temp;j--)
{
arr[j]=arr[j-1];
}
arr[j]=temp;
}
}
2、希尔排序
简介:希尔排序是在插入排序基础上改进而来,其本质也是插入排序,改进后的算法时间复杂度降到了O(n log n)。


排序机理:根据步长由长到短分组,比如步长为5,那就把间隔为5的元素取出来,算为一组进行插入排序,这组排完之后再以步长为2进行插入排序,直到步长为1为止。本质上是在插入排序上加入了间隔机制。
时间复杂度:O(n log n)
稳定性:不稳定
代码:
void shellsort(int arr[],int n)
{//希尔排序
for(int gap=n/2;gap>0;gap/=2)
{
for(int i=gap;i<n;i++)
{
int temp=arr[i];
int j;
for(j=i;j>=gap&&arr[j-gap]>temp;j-=gap)
arr[j]=arr[j-gap];
arr[j]=temp;
}
}
}
3、基数排序
简介:基数排序是分别先对数字的个位进行排序,然后十位,百位,千位,万位等等,最后一步一次性排好,其中数位不足的就要用0补全。排序过程的话,有点像这种感觉(如图)
排序机理:
时间复杂度:O(n k)
稳定性:又稳又快
代码:
int getMax(int arr[],int n)//寻找数组中最大元素
{
int mx=arr[0];
for(int i=1;i<n;i++)
if(arr[i]>mx)
mx=arr[i];
return mx;
}
void countsort(int arr[],int n,int exp)
{
int output[n];
int i,count[10]={0};
for(i=0;i<n;i++)
count[(arr[i]/exp)%10]++;//取出某一位,进行10个数字的分配
for(i=1;i<10;i++)
count[i]+=count[i-1];//count数组从1到9逐次累加前一项
for(i=n-1;i>0;i--)
{
output[count[(arr[i]/exp)%10]-1]=arr[i];//将arr中的元素按照取余的梯度直方图,依次放到合适的位置
count[(arr[i]/exp)%10]--;//该基数的剩余空位置相应减少一个
}
for(i=0;i<n;i++)
arr[i]=output[i];
}
void radixsort(int arr[],int n)
{
int m=getMax(arr,n);
for(int exp=1;m/exp>0;exp*=10)
countsort(arr,n,exp);
}
4、冒泡排序
简介:大学中学习 C++ 的第二个排序算法,很经典。
排序机理:冒泡排序顾名思义,如果把这个数组以左边为底,右边为顶,逆时针旋转90度,就像一个水中的气泡,气泡有什么特点?在水中基本就是向上匀速浮动的,而且气泡的体积在不考虑压强变化的情况下体积不变。在冒泡排序中,气泡里面有两个数字,仅将在气泡里面的两个数字进行大小比较,小的靠左,大的靠右。排完之后,气泡像上冒一格,也就是向右右移一格。当若n(n为总元素的个数)个泡泡冒完之后,也就排好序了。
时间复杂度:O(n^2)
稳定性:稳是稳,就是慢了点
代码:
void bubblesort(int a[],int n)//void bubblesort(vector& a)
{
bool swapp=true;
while(swapp)
{
swapp=false;
for(int i=0;i<n;i++)//for(size_t i=0;i
{
if(a[i]>a[i+1])
{
a[i] += a[i+1];
a[i+1] = a[i]-a[i+1];
a[i] -= a[i+1];
swapp=true;
}
}
}
}
5、快速排序
简介:简称快排,时间复杂度不固定,在最坏情况下(元素刚好是反向的)速度比较慢,达到 O(n^2),但如果在比较理想的情况下时间复杂度 O(nlogn)。快排本质也用到分治思想,快排算法每次选择一个元素并且将整个数组以那个元素分为两部分,根据实现算法的不同,元素的选择一般有如下几种:
- 永远选择第一个元素
- 永远选择最后一个元素
- 随机选择元素
- 取中间值
代码以永远选择第一个元素为例
算法机理:
时间复杂度:O(n log n)
稳定性:不稳定,速度一般
代码:
//快速排序
void exchange(int *p,int *q)
{
int temp=*p;
*p=*q;
*q=temp;
}
void quicksort(int arr[],int left,int right)
{
if(left>=right) return ;
int i=left,j=right,temp=arr[left];
while(i<j)
{
while(i<j&&arr[j]>=temp) j--;
while(i<j&&arr[i]<=temp) i++;
if(i<j) exchange(&arr[i],&arr[j]);
}
arr[left]=arr[i];//更换下一个参考数
arr[i]=temp;//参考数回到i,j之间
quicksort(arr,i+1,right);//带入递归
quicksort(arr,left,i-1);
}
6、堆排序
简介:搞清楚堆排序,首先要搞明白几个概念:最大堆,最小堆,堆源自完全二叉树,完全二叉树与满二叉树的关系,满二叉树与普通二叉树区别,普通二叉树与多叉树的特点,树的基本属性,树与无向不闭合图的关系。开玩笑的啦,其实这里面只要理解最大堆就好了,别的就当串联复习吧。
排序机理:堆排序,顾名思义是在堆的基础上进行排序。所以首先要创建一个堆,并且把初始堆调整为最大堆,这样堆中的最大数就排到了最顶端,然后,只需将最顶端的数与数组中(也是堆中)最后一位调换位置,把调换过位置的最大值称之为有序区,接着再继续把调换之后无序区的堆,调整为最大堆即可,最后连续进行n-1个循环即可实现堆排序。过程就像下图一样(图来自公众号:五分钟学算法)
实现效果就像下图一样:
时间复杂度:O(n log n)
稳定性:不太稳,速度也还行
代码:
void heapify(int arr[],int n,int i)//不断调整以保证是最大堆
{
int largest=i;
int l=2*i+1;
int r=2*i+2;
if(l<n&&arr[l]>arr[largest])//最大元素向上排
largest=l;//本质是数组的下标largest在移动
if(r<n&&arr[r]>arr[largest])
largest=r;
if(largest!=i)//递归处理子堆
{
swap(arr[i],arr[largest]);
heapify(arr,n,largest);
}
}
void heapsort(int arr[],int n)
{
for(int i=n/2-1;i>=0;i--)//建立堆
heapify(arr,n,i);
for(int i=n-1;i>=0;i--)//n-1次将堆顶最大值与有序区交换
{
swap(arr[0],arr[i]);
heapify(arr,i,0);
}
}
7 、归并排序
简介:归并排序是在前面的排序的基础上加上了分治思想,分而治之。分到什么程度?分到直到只剩1,不能再分为止。然后呢?然后再两两相比较来合并成有序的数组,将若干个这样的数组中的元素两两相比,按照大小顺序合并。
算法机理:下面用一张动态的直方图来表示这个过程,直方图中不同高低代表不同数值大小的元素。先分后后合一目了然。另外根据这个图也说明了,递归的本质就是树。
时间复杂度:O(n log n)
稳定性:稳定,速度一般
代码:
void merge(int arr[],int l,int m,int r)
{
int i,j,k;
int n1=m-l+1;//切分
int n2=r-m;
int L[n1],R[n2];
for(i=0;i<n1;i++)
L[i]=arr[l+i];
for(j=0;j<n2;j++)
R[j]=arr[m+1+j];
i=0;
j=0;
k=l;
while(i<n1&&j<n2)//合并操作
{
if(L[i]<=R[j])
{
arr[k]=L[i];
i++;
}
else
{
arr[k]=R[j];
j++;
}
k++;
}
while(i<n1)//解决两个数组比较后大小不同问题
{
arr[k]=L[i];
i++;
k++;
}
while(j<n2)
{
arr[k]=R[j];
j++;
k++;
}
}
void mergesort(int arr[],int l,int r)
{
if(l<r)
{
int m=l+(r-l)/2;
mergesort(arr,l,m);
mergesort(arr,m+1,r);
merge(arr,l,m,r);
}
}
8、选择排序
简介:选择排序是一种很简单的排序方法,直观明了。也是通过比较并通过循环调换位置来进行排序的。
算法机理:
时间复杂度:O(n^2)
稳定性:不稳定,速度慢
代码:
//选择排序
void selectionsort(int arr[],int length)
{
int temp,minindex=0;
for(int i=0;i<length;i++)
{
for(int j=i+1;j<length;j++)
if(arr[j]<arr[minindex]) minindex=j;
temp=arr[i];
arr[i]=arr[minindex];
arr[minindex]=temp;
}
}
9、计数排序
简介:计数排序作为线性时间复杂度的排序,必须具有明确的数据范围。计数排序不是基于比较的方法,而是将元素数值按储存到另外开辟数组空间内。
算法机理:
时间复杂度:O(n+k)
稳定性:稳定,速度快
代码:
void countingsort(int arr[],int maxvalue,int length)//计数排序需要提供数据范围
{
int* counting=new int[maxvalue+1]();
int a=0;
for(int i=0;i<=length;i++)
counting[arr[i]]++;
for(int i=1;i<=maxvalue;i++)
{
int temp=counting[i];
counting[i]+=counting[i-1];
while(temp--)
arr[a++]=i;
}
}
10、桶排序
简介:桶排序其实就是加强版的计数排序。桶排序的思路就是将一组数据先按照一定的规则放到不同的桶中,桶的分配一般有简单分桶和规化分桶,
- 简单分桶:桶号=max / 10 – min / 10 + 1
- 规约化分桶:桶号=(array[i] - min) / (max - min) * array.length
分完桶后,先对桶号排序,再对每个桶内的元素分别排序(这里有可能使用到别的排序方法或者是以递归方式继续用桶排序)。
排序机理:
时间复杂度:O(n+k)
稳定性:稳定,速度很快
代码:
int getmax(int arr[],int n)//寻找数组中最大元素
{
int mx=arr[0];
for(int i=1;i<n;i++)
if(arr[i]>mx)
mx=arr[i];
return mx;
}
int getmin(int arr[],int n)//寻找数组中最大元素
{
int mi=arr[0];
for(int i=1;i<n;i++)
if(arr[i]<mi)
mi=arr[i];
return mi;
}
void bucketsort(int arr[],int n)
{
vector<int> b[n]; //向量b的大小应当≥桶序号bn可能出现的最大值
int max=getmax(arr,n);
int min=getmin(arr,n);
for(int i=0;i<n;i++)
{
int bn=max/10-min/10+1;
// int bn=(arr[i]-min)/(max-min)*10;//简单分桶
// int bn=arr[i]/(N/100);//归约化分桶
// cout<
b[bn].push_back(arr[i]);//在序号为bn的桶中(序列最后)插入目标元素
}
for(int i=0;i<n;i++)//sort需要include
sort(b[i].begin(),b[i].end());
int index=0;//桶合并
for(int i=0;i<n;i++)
for(int j=0;j<b[i].size();j++)
arr[index++]=b[i][j];
}
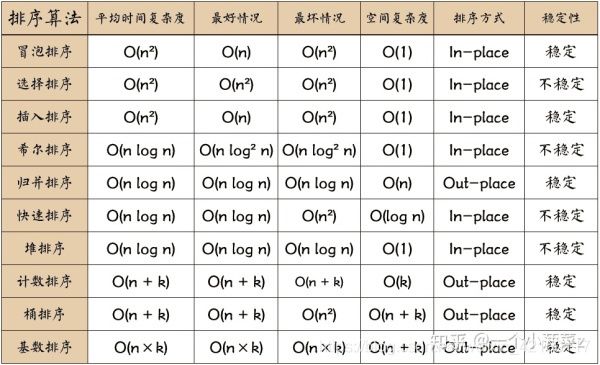
时间复杂度对比
附:调试程序
#include& a)
{
bool swapp=true;
while(swapp)
{
swapp=false;
for(int i=0;i<n;i++)//for(size_t i=0;i
{
if(a[i]>a[i+1])
{
a[i] += a[i+1];
a[i+1] = a[i]-a[i+1];
a[i] -= a[i+1];
swapp=true;
}
}
}
}
//归并排序
void merge(int arr[],int l,int m,int r)
{
int i,j,k;
int n1=m-l+1;//切分
int n2=r-m;
int L[n1],R[n2];
for(i=0;i<n1;i++)
L[i]=arr[l+i];
for(j=0;j<n2;j++)
R[j]=arr[m+1+j];
i=0;
j=0;
k=l;
while(i<n1&&j<n2)//合并操作
{
if(L[i]<=R[j])
{
arr[k]=L[i];
i++;
}
else
{
arr[k]=R[j];
j++;
}
k++;
}
while(i<n1)//解决两个数组比较后大小不同问题
{
arr[k]=L[i];
i++;
k++;
}
while(j<n2)
{
arr[k]=R[j];
j++;
k++;
}
}
void mergesort(int arr[],int l,int r)
{
if(l<r)
{
int m=l+(r-l)/2;
mergesort(arr,l,m);
mergesort(arr,m+1,r);
merge(arr,l,m,r);
}
}
/
//堆排序
void heapify(int arr[],int n,int i)//不断调整以保证是最大堆
{
int largest=i;
int l=2*i+1;
int r=2*i+2;
if(l<n&&arr[l]>arr[largest])//最大元素向上排
largest=l;//本质是数组的下标largest在移动
if(r<n&&arr[r]>arr[largest])
largest=r;
if(largest!=i)//递归处理子堆
{
swap(arr[i],arr[largest]);
heapify(arr,n,largest);
}
}
void heapsort(int arr[],int n)
{
for(int i=n/2-1;i>=0;i--)//建立堆
heapify(arr,n,i);
for(int i=n-1;i>=0;i--)//n-1次将堆顶最大值与有序区交换
{
swap(arr[0],arr[i]);
heapify(arr,i,0);
}
}
/
//桶排序
int getmax(int arr[],int n)//寻找数组中最大元素
{
int mx=arr[0];
for(int i=1;i<n;i++)
if(arr[i]>mx)
mx=arr[i];
return mx;
}
int getmin(int arr[],int n)//寻找数组中最大元素
{
int mi=arr[0];
for(int i=1;i<n;i++)
if(arr[i]<mi)
mi=arr[i];
return mi;
}
void bucketsort(int arr[],int n)
{
vector<int> b[n]; //向量b的大小应当≥桶序号bn可能出现的最大值
int max=getmax(arr,n);
int min=getmin(arr,n);
for(int i=0;i<n;i++)
{
int bn=max/10-min/10+1;
// int bn=(arr[i]-min)/(max-min)*10;//简单分桶
// int bn=arr[i]/(N/100);//归约化分桶
// cout<
b[bn].push_back(arr[i]);//在序号为bn的桶中(序列最后)插入目标元素
}
for(int i=0;i<n;i++)//sort需要include
sort(b[i].begin(),b[i].end());
int index=0;//桶合并
for(int i=0;i<n;i++)
for(int j=0;j<b[i].size();j++)
arr[index++]=b[i][j];
}
///
//计数排序
void countingsort(int arr[],int maxvalue,int length)//计数排序需要提供数据范围
{
int* counting=new int[maxvalue+1]();
int a=0;
for(int i=0;i<=length;i++)
counting[arr[i]]++;
for(int i=1;i<=maxvalue;i++)
{
int temp=counting[i];
counting[i]+=counting[i-1];
cout<<i<<'\t'<<temp<<'\t'<<counting[i]<<'\t'<<'\t';
while(temp--)
{
arr[a++]=i;
}
}
}
//选择排序
void selectionsort(int arr[],int length)
{
int temp,minindex=0;
for(int i=0;i<length;i++)
{
for(int j=i+1;j<length;j++)
if(arr[j]<arr[minindex]) minindex=j;
temp=arr[i];
arr[i]=arr[minindex];
arr[minindex]=temp;
}
}
///
//快速排序
void exchange(int *p,int *q)
{
int temp=*p;
*p=*q;
*q=temp;
}
void quicksort(int arr[],int left,int right)
{
if(left>=right) return ;
int i=left,j=right,temp=arr[left];
while(i<j)
{
while(i<j&&arr[j]>=temp) j--;
while(i<j&&arr[i]<=temp) i++;
if(i<j) exchange(&arr[i],&arr[j]);
}
arr[left]=arr[i];//更换下一个参考数
arr[i]=temp;//参考数回到i,j之间
quicksort(arr,i+1,right);//带入递归
quicksort(arr,left,i-1);
}
int main()
{//以下注释默认N=10000
int a[N];//几乎不消耗时间
for(int i=0;i<N;i++)//消耗约200ms
a[i]=rand()%N;
for(int i=0;i<N;i++)//消耗约5000ms
{
cout<<a[i]<<'\t';
if((i+1)%15==0) cout<<'\n';
}
cout<<endl<<endl;
clock_t start=clock();//clock返回当前次数
//insertion_sort(a,N);// 插入排序消耗约112ms
//shellsort(a,N) ;//希尔排序约2ms
//radixsort(a,N);//基数排序 4ms
//bubblesort(a,N);//冒泡排序1157ms
//mergesort(a,0,N);//归并排序5ms
//heapsort(a,N); //堆排序3ms
//bucketsort(a,N);//桶排序5ms
//countingsort(a,N,N);//计数排序0ms
//selectionsort(a,N);//选择排序204ms
quicksort(a,0,N); //快速排序
clock_t end =clock();
for(int i=0;i<N;i++)//消耗约4700ms
{
cout<<a[i]<<'\t';
if((i+1)%15==0) cout<<'\n';
}
cout<<endl<<"耗时:"<<(double)(end-start)/CLOCKS_PER_SEC<<"s"<<endl;
return 0;
}