小白试水——leetcode腾讯题库-11.盛最多水的容器（Python解答）

题目11：盛最多水的容器

给定 n 个非负整数 $a_1，a_2，...，a_n$，每个数代表坐标中的一个点 ($i,a_i$) 。在坐标内画 $n$ 条垂直线，垂直线 $i$ 的两个端点分别为 ($i,a_i$) 和 ($i,0$)。找出其中的两条线，使得它们与 $x$ 轴共同构成的容器可以容纳最多的水。

说明：你不能倾斜容器，且 $n$ 的值至少为 2。

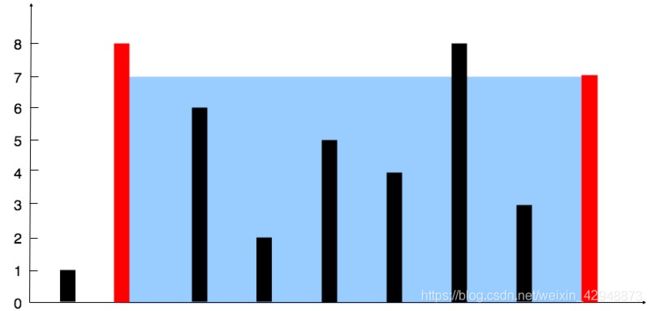
图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下，容器能够容纳水（表示为蓝色部分）的最大值为 49。

示例:

输入: [1,8,6,2,5,4,8,3,7]
输出: 49

代码实现(笨拙)

根据两头遍历列表求取每个数据对应的面积，再提取最大值

# 此代码遇到较大数据时易出现运行超时及内存溢出
class Solution(object):
    def maxArea(self, height):
        """
        :type height: List[int]
        :rtype: int
        """
        list = []
        if len(height) >=2:
            for i in range(len(height)):
                for j in range(len(height)-1,i,-1):
                    if i < j:
                        if height[i] <= height[j]:
                            list.append(height[i]*len(height[i:j]))
                        else:
                            list.append(height[j]*len(height[i:j]))
        return max(list)

代码优化

class Solution(object):
    def maxArea(self, height):
        """
        :type height: List[int]
        :rtype: int
        """
        area = 0
        for i in range(len(height)-1):
            for j in range(len(height)-1,i,-1):
                area = max(area,min(height[i],height[j])*(j-i))
        return area

最终代码

class Solution(object):
    def maxArea(self, height):
        """
        :type height: List[int]
        :rtype: int
        """
        area = 0
        i = 0
        j = len(height)-1
        while i < j:
            area = max(area,min(height[i],height[j])*(j-i))
            if height[i] < height[j]:
                i += 1
            else:
                j -= 1
        return area

解析

双指针法

算法

这种方法背后的思路在于，两线段之间形成的区域总是会受到其中较短那条长度的限制。此外，两线段距离越远，得到的面积就越大。

我们在由线段长度构成的数组中使用两个指针，一个放在开始，一个置于末尾。 此外，我们会使用变量 maxarea 来持续存储到目前为止所获得的最大面积。 在每一步中，我们会找出指针所指向的两条线段形成的区域，更新 maxarea，并将指向较短线段的指针向较长线段那端移动一步。

查看下面的例子将有助于你更好地理解该算法：

1 8 6 2 5 4 8 3 7

第一步：

第二步：

第三步：

依次类推，最终得到最大面积。

这种方法如何工作？
最初我们考虑由最外围两条线段构成的区域。现在，为了使面积最大化，我们需要考虑更长的两条线段之间的区域。如果我们试图将指向较长线段的指针向内侧移动，矩形区域的面积将受限于较短的线段而不会获得任何增加。但是，在同样的条件下，移动指向较短线段的指针尽管造成了矩形宽度的减小，但却可能会有助于面积的增大。因为移动较短线段的指针会得到一条相对较长的线段，这可以克服由宽度减小而引起的面积减小。

LeetCode效果显示