python张正友相机标定

这里给出我觉得原理解释较清楚的地址，供大家参考：
https://blog.csdn.net/u010128736/article/details/52860364
这一篇为张正友标定原版论文的翻译版：
https://blog.csdn.net/heroacool/article/details/50286677?tdsourcetag=s_pctim_aiomsg
下面所写的原理均参考转载自这两篇文章，有问题请指正。

(一)基本原理

1. 相机标定简单来说，是一个从世界坐标系→相机坐标系→成像平面坐标系→像素平面坐标系，也就是一个从三维点转换到三维点再到二维点的过程。进行摄像机标定的目的：求出相机的内、外参数，以及畸变参数。
2. 基本参数设定
   s: 世界坐标系到图像坐标系的尺度因子
   (u0,v0): 像主点坐标
   α, β: 焦距与像素横纵比的融合
   γ: 径向畸变参数
   2D 图像点：m=[u,v,1]T
   3D 空间点：X=[X,Y,Z,1]T
   标定用的棋盘格平面到图像平面的单应性关系为：
   
   其中[R,T]为外参，A为相机内参矩阵
   
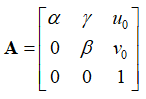
3. 不妨设棋盘格位于Z = 0，定义旋转矩阵R的第i列为 ri, 则有：
   
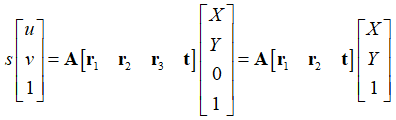
   于是空间到图像的映射可改为：
   
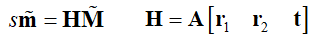
   其中H 是描述Homographic矩阵,可通过最小二乘，从角点世界坐标到图像坐标的关系求解。
   令 H 为 H = [h1 h2 h3]，
   
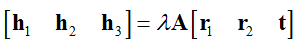
   Homography 有 8 个自由度，通过上述等式的矩阵运算，根据正交和归一化的约束可以得到如下等式：
   
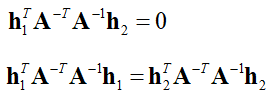
   这个条件下，我们只能得到两个内参的约束条件。
4. 外部参数可通过Homography求解，由 H = [h1 h2 h3] = λA[r1 r2 t]，可推出
   
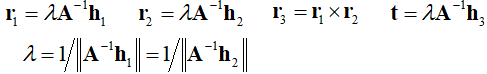
   一般而言，求解出的R = [r1 r2 r3] 不会满足正交与归一的标准，在实际操作中，R 可以通过SVD分解实现规范化。给定 n 张棋盘格图像，每张图像有 m 个角点，最小化下述公式等同于极大似然估计：
   
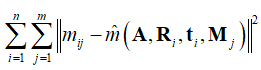
5. 张氏标定法只关注了影响最大的径向畸变。则数学表达式为：
   
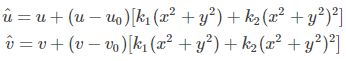
   其中，(u,v)是理想无畸变的像素坐标，(u^,v)(u^,v)是实际畸变后的像素坐标。(u0,v0)代表主点，(x,y)是理想无畸变的连续图像坐标，(x^,y)(x^,y)是实际畸变后的连续图像坐标。k1和k2为前两阶的畸变参数。
6. 这里的原理只有部分，开头给出的原论文介绍得更详细清楚，这里就不多做介绍了避免误导大家。
7. 实验操作步骤：
   （1）打印一张棋盘格A4纸张（黑白间距已知），并贴在一个平板上
   （2）针对棋盘格拍摄若干张图片（一般10-20张）
   （3）在图片中检测特征点（Harris特征）
   （4）利用解析解估算方法计算出5个内部参数，以及6个外部参数
   （5）根据极大似然估计策略，设计优化目标并实现参数的refinement

（二）运行结果与分析

1. 过程中可能出现的问题
   (1)ValueError: could not broadcast input array from shape (54,2) into shape (49,2)
   在运行过程中，我们所要采用计算的是棋盘格的内角点，而不包括外角点，若是出现这种错误可以检查看看自己函数中所代入的角点是否有误。
   (2)error: ..\..\..\modules\core\src\array.cpp:2482: error: (-206) Unrecognized or unsupported array type in function cvGetMat
   这个错误也只是个小错误，需要检查自己的图片路径是否有误。若是有出现cv2error，-215这样错误的，可能是opencv版本与代码不适用，可以尝试换个opencv版本。

2. 测试图片：
   

3. 运行结果
   
   （1）我所使用的手机型号为OPPO r11，相机分辨率为3456×4608，焦距为4.27mm，拍摄使用的棋盘格单个方格尺寸为2.5cm×2.5cm，每行每列均有10个方格。
   （2）intrinsics_parm为内参，一个相机只有一个内参，distortionk为畸变系数K，extrinsics_parm为外参数，接下来的数据则为每一张图片的参数，因为拍摄角度的不同所以每一张的外参也不相同，有17张图片就有17个外参。
   （3）在这里，要注意的是所使用的图片要先转为灰度图再运行，因为原图所占空间较大怕影响处理速度，所以我使用的图像是经过比例压缩的，若是不经过比例压缩会导致图像变形，方格就没那么精确，结果也会有较大的偏差。

（三）代码

若是使用要做相应的修改，比如10×10的棋盘，则内角点为9×9。

#!usr/bin/env/ python
# _*_ coding:utf-8 _*_

import cv2 as cv
import numpy as np
import os
from step.homography import get_homography
from step.intrinsics import get_intrinsics_param
from step.extrinsics import get_extrinsics_param
from step.distortion import get_distortion
from step.refine_all import refinall_all_param


def calibrate():
    #求单应矩阵
    H = get_homography(pic_points, real_points_x_y)

    #求内参
    intrinsics_param = get_intrinsics_param(H)

    #求对应每幅图外参
    extrinsics_param = get_extrinsics_param(H, intrinsics_param)

    #畸变矫正
    k = get_distortion(intrinsics_param, extrinsics_param, pic_points, real_points_x_y)

    #微调所有参数
    [new_intrinsics_param, new_k, new_extrinsics_param]  = refinall_all_param(intrinsics_param,
                                                            k, extrinsics_param, real_points, pic_points)

    print("intrinsics_parm:\t", new_intrinsics_param)
    print("distortionk:\t", new_k)
    print("extrinsics_parm:\t", new_extrinsics_param)


if __name__ == "__main__":
    file_dir = r'..\image6'
    # 标定所用图像
    pic_name = os.listdir(file_dir)

    # 由于棋盘为二维平面，设定世界坐标系在棋盘上，一个单位代表一个棋盘宽度，产生世界坐标系三维坐标
    cross_corners = [7, 7] #棋盘方块交界点排列
    real_coor = np.zeros((cross_corners[0] * cross_corners[1], 3), np.float32)
    real_coor[:, :2] = np.mgrid[0:7, 0:7].T.reshape(-1, 2)

    real_points = []
    real_points_x_y = []
    pic_points = []

    for pic in pic_name:
        pic_path = os.path.join(file_dir, pic)
        pic_data = cv.imread(pic_path)

        # 寻找到棋盘角点
        succ, pic_coor = cv.findChessboardCorners(pic_data, (cross_corners[0], cross_corners[1]), None)

        if succ:
            # 添加每幅图的对应3D-2D坐标
            pic_coor = pic_coor.reshape(-1, 2)
            pic_points.append(pic_coor)

            real_points.append(real_coor)
            real_points_x_y.append(real_coor[:, :2])
    calibrate()

以上为主函数，代码原作者还写了一些子函数调用，具体参考 https://github.com/SPengLiang/Camera-Calibration-of-Zhang-s-method