Week 12 作业

A - 必做题 - 1

给出n个数，zjm想找出出现至少(n+1)/2次的数， 现在需要你帮忙找出这个数是多少？

输入

本题包含多组数据：
每组数据包含两行。
第一行一个数字N(1<=N<=999999) ，保证N为奇数。
第二行为N个用空格隔开的整数。
数据以EOF结束。

输出

对于每一组数据，你需要输出你找到的唯一的数。

样例输入

5
1 3 2 3 3
11
1 1 1 1 1 5 5 5 5 5 5
7
1 1 1 1 1 1 1

样例输出

3
5
1

思路

综述

最初：想的是没有说数据范围，想必可能超过int，所以干脆开了long long.于是写了个O(n^2)的算法，直接导致TLE；
改进：开1e6的数组来存储，i索引号对应的数字是数字i出现次数。

总结

最初拿到这个题感觉有点小坑：没有说数据范围，直接导致了第一次提交超时：（想必应该是题目不够严谨）

代码

#include 
#include 
#include 
using namespace std;
int N;
const int maxn = 1e6;
int a[maxn];
int term;
void init(){for(int i=0;i<1e6;i++)a[i]=0;}

int main(){
	while(cin>>N){
		init();
		for(int i=0;i<N;i++){
			cin>>term;
			a[term]++;
		}
		
		int num = (N+1)/2; 
		
		for(int i=0;i<1e6;i++){
			if(a[i]>=num){
				cout<<i<<endl;
				break;
			}
		}
	}
}

B - 必做题 - 2 三维bfs搜索

zjm被困在一个三维的空间中,现在要寻找最短路径逃生！
空间由立方体单位构成。
zjm每次向上下前后左右移动一个单位需要一分钟，且zjm不能对角线移动。
空间的四周封闭。zjm的目标是走到空间的出口。
是否存在逃出生天的可能性？如果存在，则需要多少时间？

输入

输入第一行是一个数表示空间的数量。
每个空间的描述的第一行为L，R和C（皆不超过30）。
L表示空间的高度，R和C分别表示每层空间的行与列的大小。
随后L层，每层R行，每行C个字符。
每个字符表示空间的一个单元。’#‘表示不可通过单元，’.‘表示空白单元。
zjm的起始位置在’S’，出口为’E’。每层空间后都有一个空行。
L，R和C均为0时输入结束。

输出

每个空间对应一行输出。
如果可以逃生，则输出如下
Escaped in x minute(s).
x为最短脱离时间。
如果无法逃生，则输出如下
Trapped!

样例输入

    3 4 5
    S….
    .###.
    .##..
    ###.#

    #####
    #####
    ##.##
    ##…

    #####
    #####
    #.###
    ####E

    1 3 3
    S##
    #E#
    ###

    0 0 0

样例输出

Escaped in 11 minute(s).
Trapped!

思路

综述

bfs搜索的模板题；
最初拿到题目的时候有点蒙。细细思考发现和二维空间并无差异。
不可以用dfs，dfs可以找到出口，但是找不到最短的路线。

总结&&拓展

二维地图可以轻易拓展到三维；
于是n维空间的种种题目也可以类比做出。

踩踩坑

scanf("%c",ch);这样会读入空格和回车符
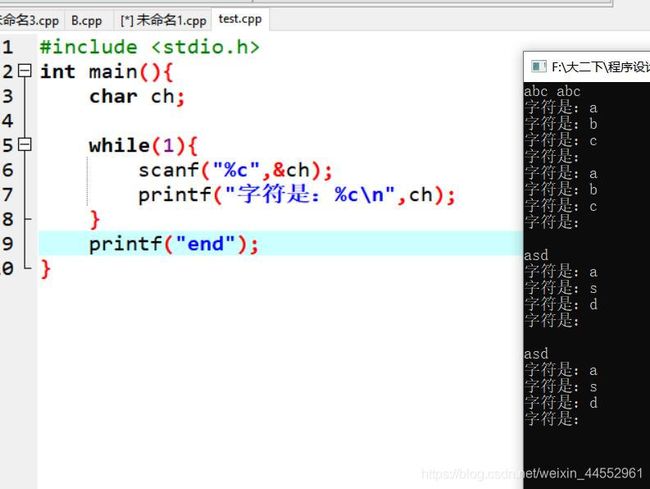以下两种写法可以忽略回车符和空格

cin>>ch;
scanf(" %c",&ch);

代码

#include 
#include 
#include 
using namespace std;
struct node{
	int x,y,z,step;
	node(){
		step=0;
	}
};

char mp[40][40][40];
int vis[40][40][40];
int L,R,C;//L-->x  R-->y  C-->z
int sx,sy,sz;
int ex,ey,ez;
//依次是 上下东西南北 
int dx[] = {0,0,0,0,1,-1};
int dy[] = {0,0,1,-1,0,0};
int dz[] = {1,-1,0,0,0,0};

int check(node thenode){
	if(thenode.x < 0 || thenode.x >= L)return 1;
	if(thenode.y < 0 || thenode.y >= R)return 1;
	if(thenode.z < 0 || thenode.z >= C)return 1;
	if(mp[thenode.x][thenode.y][thenode.z]=='#')return 1;
	if(vis[thenode.x][thenode.y][thenode.z])return 1;
	return 0;
}

int bfs(){
	memset(vis,0,sizeof(vis));
	queue<node> qq;
	
	while(!qq.empty())qq.pop();
	
	node Node;
	Node.x = sx,Node.y = sy,Node.z = sz,Node.step=0;
	qq.push(Node);
	
	while(!qq.empty()){
		node now = qq.front();
		qq.pop();
		//找到出口 
		if( ex==now.x && ey==now.y && ez==now.z ){
			return now.step;
		}		
		//遍历六个方向 
		node next; 
		for(int i=0;i<6;i++){
			next.x = now.x + dx[i];
			next.y = now.y + dy[i];
			next.z = now.z + dz[i];
			next.step = now.step+1;
			
			
			if(check(next))continue;//判断是否可行 
			
			vis[next.x][next.y][next.z] = 1;
			qq.push(next);
			
		}
		
	}
	return 0;
}


int main(){
	
	while(1){
		cin>>L>>R>>C;
		if(L==0 && R==0 && C==0)break;
		
		for(int i=0;i<L;i++){
			for(int j=0;j<R;j++){
				scanf("%s",mp[i][j]);
				for(int k=0;k<C;k++){
					
					if(mp[i][j][k]=='S'){
						sx = i;
						sy = j;
						sz = k;
					}if(mp[i][j][k]=='E'){
						ex = i;
						ey = j;
						ez = k;						
					}
				}
			}
		}
		
		int flag = bfs();
		
		if(flag==0 ){
			cout<<"Trapped!"<<endl;
		}else{
			printf("Escaped in %d minute(s).\n",flag);
		}
		
	}
	
}

C - 必做题 - 3 m段最长子串

东东每个学期都会去寝室接受扫楼的任务，并清点每个寝室的人数。
每个寝室里面有ai个人(1<=i<=n)。从第i到第j个宿舍一共有sum(i,j)=a[i]+…+a[j]个人
这让宿管阿姨非常开心，并且让东东扫楼m次，每一次数第i到第j个宿舍sum(i,j)
问题是要找到sum(i1, j1) + … + sum(im,jm)的最大值。且ix <= iy <=jx和ix <= jy <=jx的情况是不被允许的。也就是说m段都不能相交。
注：1 ≤ i ≤ n ≤ 1e6 , -32768 ≤ ai ≤ 32767 人数可以为负数。。。。(1<=n<=1000000)

输入

输入m，输入n。后面跟着输入n个ai 处理到 EOF

输出

输出最大和

样例输入

1 3 1 2 3
2 6 -1 4 -2 3 -2 3

样例输出

6
8 

思路

综述

该题用到方法有：dp+滚动数组；
题意归结为一句话就是m段最长子串问题；
难点就在定状态和状态转移方程以及滚动数组的应用。

状态定义

dp[i][j]表示前j个数据共i个区间所能取到的最大值；（注意其中第a[j]包含在内）

状态转移：

（注意其中第a[j]包含在内）

dp[i][j] = max(dp[i][j-1]+a[j] , dp[i-1][k] + a[j])(1<=k<=j-1)

总结

动态规划感觉有这么一个流程
写出最原始的状态定义和状态转移方程->滚动数组进行优化空间复杂度->其他方面优化时间复杂度
直接贴出多次不成功代码，供学习借鉴

最原始的没有滚动数组的

#include 
#include 
#include 

using namespace std;

int n,m;
const int maxn = 1e6+10;
const int maxm = 100;
int a[maxn];
int dp[maxm][maxn];
int dpmax[maxn];

void init(){
    memset(dp,0,sizeof(dp));
    memset(dpmax,0,sizeof(dpmax));
}

void in(){
    for(int i=1;i<=n;i++)
    {
        scanf("%d",&a[i]);
    }


}

void work()
{
    //work
    for(int i=1;i<=m;i++)
    {
        for(int j=1;j<=n;j++)
        {
        	dp[i][j] = dp[i][j-1] + a[j];

            for(int k=i-1;k<=j-1;k++){
                dp[i][j] = max(dp[i][j],dp[i-1][k]);
            }
			
        }
    }
    
    
    int ans = -123;
    for(int i=m;i<=n;i++)ans = max(dp[m][i],ans);
    cout<<ans<<endl; 
    // cout<
}


int main(){
    while(scanf("%d%d",&m,&n)!=EOF)
    {
        init();
        in();
        work();

	}
    

}

添加滚动数组，但是超时

#include 
#include 
#include 

using namespace std;

int n,m;
const int maxn = 1e6+10;
const int maxm = 100;
int a[maxn];
int dp[maxn][2];
int dpmax[maxn];

void init(){
    memset(dp,0,sizeof(dp));
    memset(dpmax,0,sizeof(dpmax));
}

void in(){
    for(int i=1;i<=n;i++)
    {
        scanf("%d",&a[i]);
    }


}

void work()
{
	int now = 0;
	dp[1][now] = a[1];
    for(int i=2;i<=n;i++) dp[i][now] = max(dp[i-1][now]+a[i],a[i]);
	now = !now; 
	//work
    for(int i=1;i<=m;i++)
    {
        for(int j=1;j<=n;j++)
        {
        	dp[j][now] = dp[j-1][now] + a[j];

            for(int k=i-1;k<=j-1;k++){
                dp[j][now] = max(dp[j][now],dp[k][!now]);
            }
			
        }
        now = !now;
    }
    
    
    int ans = -123;
    for(int i=m;i<=n;i++)ans = max(dp[i][now],ans);
    cout<<ans<<endl; 

}


int main(){
    while(scanf("%d%d",&m,&n)!=EOF)
    {
        init();
        in();
        work();

	}
    

}

完整的代码

#include 
using namespace std;
int n,m;
const int maxn = 1e6+50;
int dp[maxn];
int num[maxn];

int calc(){
	int term=0;
	for(int i=1;i<=m;i++){
		 
		term=0;
		for(int k=1;k<=i;k++)term+=num[k];
		dp[n] = term;
		for(int j=i+1;j<=n;j++){
			if(term<dp[j-1]) term = dp[j-1];
			term += num[j];
			dp[j-1] = dp[n];
			if(term>dp[n])dp[n]=term;
		}
	}
	return dp[n];
	
}

int main(){
 	while(scanf("%d%d",&m,&n)!=EOF){
		for(int i=1;i<=n;i++){
			scanf("%d",&num[i]);
			dp[i] = 0;
			 
		} 
		printf("%d\n",calc());
	} 
}

D - 选做题 - 1

We give the following inductive definition of a “regular brackets” sequence:
the empty sequence is a regular brackets sequence,
if s is a regular brackets sequence, then (s) and [s] are regular brackets sequences, and
if a and b are regular brackets sequences, then ab is a regular brackets sequence.
no other sequence is a regular brackets sequence
For instance, all of the following character sequences are regular brackets sequences:
(), [], (()), ()[], ()[()]
while the following character sequences are not:
(, ], )(, ([)], ([(]
Given a brackets sequence of characters a1a2 … an, your goal is to find the length of the longest regular brackets sequence that is a subsequence of s. That is, you wish to find the largest m such that for indices i1, i2, …, im where 1 ≤ i1 < i2 < … < im ≤ n, ai1ai2 … aim is a regular brackets sequence.
Given the initial sequence ([([]])], the longest regular brackets subsequence is [([])].

输入

The input test file will contain multiple test cases. Each input test case consists of a single line containing only the characters (, ), [, and ]; each input test will have length between 1 and 100, inclusive. The end-of-file is marked by a line containing the word “end” and should not be processed.

输出

For each input case, the program should print the length of the longest possible regular brackets subsequence on a single line.

样例输入

((()))
()()()
([]])
)[)(
([][][)
end

样例输出

6
6
4
0
6

思路

综述

课上例题，是正常的动态规划，没有用到滚动数组之类的；

状态定义

总结共两种情况：

f[i][j]表示子序列[i,j]变成合法序列需要添加的最少括号的数量。
最终答案就应该是f[1][n]

状态转移

总结共两种情况：

* f[i][j] = min{f[i][k] + f[k+1][j]},( i≤k<j)
* 若S形如[S’]或(S’) ,那么f[i][ j] = min{f[i+1][ j-1]}

总结

动态规划的经典例题，动态规划题目最开始没有入门，做题多了之后发现有章可循；

坑点

初始化问题：
以后都单独写一个函数，多组数据之间需要初始化的变量都统一进行处理，这样不容易遗漏之类的；

void init(){
	//初始化，因为合法数据是j>i所以，不需要初始化上三角 
	for(int i=0;i<110;i++)
		for(int j=0;j<110;j++)
			dp[i][j]=0;
}

match匹配函数
注意有两组可能

int match(int i,int j){
	if( (s[i]=='('&&s[j]==')') || (s[i]=='['&&s[j]==']') ){
		return 1;
	}
	return 0;
}

代码

#include 
#include 
#include 
#include 
#include 
#include 
using namespace std;

string s;
int dp[110][110];

int match(int i,int j){
	if( (s[i]=='('&&s[j]==')') || (s[i]=='['&&s[j]==']') ){
		return 1;
	}
	return 0;
}
void init(){
	//初始化，因为合法数据是j>i所以，不需要初始化上三角 
	for(int i=0;i<110;i++)
		for(int j=0;j<110;j++)
			dp[i][j]=0;
}
int calc(){
	int n = s.size();
	for(int i=0;i<n-1;i++)
		dp[i][i+1] = match(i,i+1);
	for(int len=2;len<=n-1;len++){
		for(int i = 0 , j ; (j=i+len) < n ;i++){
			dp[i][j] = dp[i+1][j-1]+match(i,j);
			for(int k=i;k<j;k++)			
				dp[i][j] = max(dp[i][j],dp[i][k]+dp[k+1][j]);
				
		}
	} 
	return dp[0][n-1];
}
int main(){
	while(1){
		cin>>s;
		if(s=="end")break;
		init();
		int num = calc();
		num*=2; 
		cout<<num<<endl;
	}
}

E - 选做题 - 2

马上假期就要结束了，zjm还有 n 个作业，完成某个作业需要一定的时间，而且每个作业有一个截止时间，若超过截止时间，一天就要扣一分。
zjm想知道如何安排做作业，使得扣的分数最少。
Tips: 如果开始做某个作业，就必须把这个作业做完了，才能做下一个作业。

输入

有多组测试数据。第一行一个整数表示测试数据的组数
第一行一个整数 n(1<=n<=15)
接下来n行，每行一个字符串(长度不超过100) S 表示任务的名称和两个整数 D 和 C，分别表示任务的截止时间和完成任务需要的天数。
这 n 个任务是按照字符串的字典序从小到大给出。

输出

每组测试数据，输出最少扣的分数，并输出完成作业的方案，如果有多个方案，输出字典序最小的一个。

样例输入

2
3
Computer 3 3
English 20 1
Math 3 2
3
Computer 3 3
English 6 3
Math 6 3

样例输出

2
Computer
Math
English
3
Computer
English
Math

综述

是一道动态规划的题目；动态规划里面的状压dp；
主要是因为对于某些题目来说，状态尤其复杂，如果使用先前的多维数组 来表示，将会导致数组维度非常大，可操作性非常低
因此我们考虑使用一些编码技术，比如二进制编码，用一个数字来 表示一个状态，实现状态压缩的目的

关于位运算：

状态

f[S] 表示完成 S 作业集合后被扣的最少分数

假设S是5则转换为二进制就是101说明该状态完成了作业1和作业3；

转移方程

• sum = S 作业集合对应的总时间
• f[S|(1<<x)] = f[S] + tmp（作业 x 被扣的分数） 
• c[x] = 作业 x 完成所需时间 
• d[x] = 作业 x 的 DDL 
• tmp = max ( sum + c[x] – d[x], 0 )

如何保证字典序最小

跟学长学到的套路，这类题可以按字典序排序试试，可能会有奇效；

SUM求法

注意sum在代码里面经常出现，但是求解的过程复杂，将其剥离开来，单独为一个子函数，增加可读性；

int sum(int node){
	int time=0;
	int cnt=1;
	for(int i=1;i <= (1<<n)-1;i<<=1){
		
		if(node & i){
			time += TASK[cnt-1].day;
		}
		cnt++;
	}

return time;
}

总结

最近养成的风格：
main函数里面将大部分的操作都分离开，这样一目了然，清晰爽快；

int main(){
	cin>>T;
	while(T--){
		init();
		in();
		work();
		cout<<ans[(1<<n)-1]<<endl;
		print((1<<n)-1);
	}
}

注意

注意print里面的状态还是某个作业的区分，一开始的时候入坑了。（没区分好状态和作业）

void print(int node){
	if(node == 0) return;
	print( node - ( 1 << way[node] ) );
	cout<<TASK[way[node]].name<<endl;
}

代码

上文有详细注释

#include 
#include 
#include  
#include 
#include  
#include 
#include 
using namespace std;
const int maxn = (1<<15) + 50;
struct task{
	int ddl;
	int day;
	string name;
	bool operator < (const task & P)const{
		return name > P.name; 
	}
};

int T,n,m;
vector<task> TASK;
int way[maxn];
//int sum[maxn];
int ans[maxn];

void init(){
	TASK.clear();
	memset(ans,63,sizeof(ans));
	memset(way,0,sizeof(way));
}

void in(){
	cin>>n;
	task tempt;
	for(int i=0;i<n;i++){
		cin>>tempt.name>>tempt.ddl>>tempt.day;
		TASK.push_back(tempt);
	}
}

int sum(int node){
	int time=0;
	int cnt=1;
	for(int i=1;i <= (1<<n)-1;i<<=1){
		
		if(node & i){
			time += TASK[cnt-1].day;
		}
		cnt++;
	}

return time;
}

void work(){
	sort(TASK.begin(),TASK.end());
	ans[0]=0;
	int now;
	
	for(int S=1;S <= ( 1 << n ) - 1;S++){
		for(int i=0;i<TASK.size();i++){
			if( S & (1<<i) ){
				now = ans[S - (1<<i)] + max( sum(S - (1<<i)) + TASK[i].day - TASK[i].ddl , 0 );
				if(now < ans[S]){
					ans[S] = now;
					way[S] = i;
				} 
			}
		}
	}
}

void print(int node){
	if(node == 0) return;
	print( node - ( 1 << way[node] ) );
	cout<<TASK[way[node]].name<<endl;
}

int main(){
	cin>>T;
	while(T--){
		init();
		in();
		work();
		cout<<ans[(1<<n)-1]<<endl;
		print((1<<n)-1);
	}
}