动态规划解决曼哈顿游客问题
曼哈顿游客问题 (Manhattan Tourist Problem)
问题背景
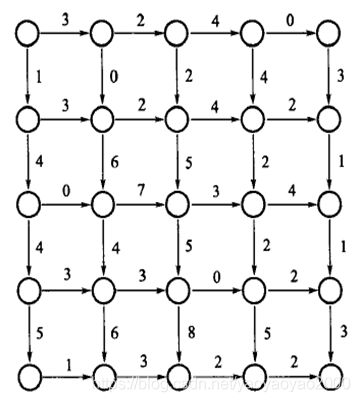
设想有个观光团在纽约曼哈顿区,并决定从位于第59街与第8大道交叉处步行至第42街与莱克星顿大道交叉处。途中会有许多景点,游客想游览尽可能多的景点。在每个街道的交叉口游客只能向东或向南步行。即使如此,他们也有很多路线可供选择。
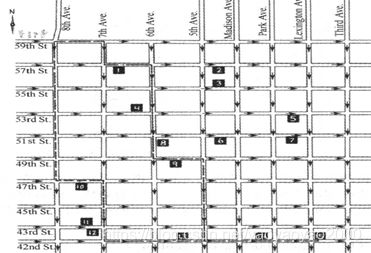
问题描述
在加权网格中选好一条最长的路线.
输入: 有源点和终点的加权网格G.
输出: G中从源点到终点的一条最长的路线.
设计、分析并实现基于动态规划技术的曼哈顿游客问题求解算法.
思路
首先,设A[i,j]为到达该点的距离,i表示从上方到达该点的距离,j表示从左边到达该点的距离;设B[i,j]存储在矩阵中前进的符号,←表示该点结果是从左边那点到这点计算得出的,即从左边到该点距离最长,↑表示该点结果是从上面那点到这点计算得出的,即从上面到该点距离最长;设C[i,j]为从起始点到该点的最短距离。
解决动态规划问题的两个条件是优化子结构和重叠子问题。这两个条件曼哈顿问题都符合。
到达某一点的距离等于,到达该点上面那一点的距离加上上面那一点距离到这一点距离,和到达该点左边那一点的距离加上左边那一点距离到这一点距离的最大值,得证曼哈顿问题存在优化子结构。
每计算出一个矩阵C[i,j]中的元素,可以重复利用它来计算它右边的点和下面的点,得证重叠子问题。
根据以上证明,我们可以抽象出以下递推公式:
C[i,j]=0,if i=0 and j=0; C[i,j]=C[i,j-1]+a_j ,if i=0 and j!=0;
C[i,j]=C[i-1,j]+a_i ,if i!=0 and j=0;
C[i,j]=MAX{C[i,j-1]+a_j,C[i-1,j]+a_i },if i!=0 and j!=0;
在构造完矩阵B[i,j],C[i,j]之后,可以使用递归的方式构造优化解,从B[m,n]开始搜索,按照箭头所指的方向去搜索。如果箭头是←,则表示到达该点需要向右走;如果箭头是↑,则表示到达该点需要向下走。
如果从左边到达该点和从右边到达该点距离相等,则默认可以从上面到达该点。
伪代码
算法输入:从上面或左边到点(i,j)的距离矩阵A[i,j]
算法输出:点(i,j)的结果来源方向矩阵B[i,j]
到点(i,j)的最长距离矩阵C[i,j]
Construct-MTP(A[i,j])
C[0,0]←0;
For x←1 To i Do
C[x,0]←C[x-1,0]+a_x;
B[x,0]←"←";
For y←1 To j Do
C[0,y]←C[0,y-1]+a_y;
B[0,y]←"↑";
For x←1 To i Do
For y←1 To j Do
If C[x,y-1]+a_y ≥ C[x-1,y]+a_x
Then C[x,y]←C[x,y-1]+a_y;
B[x,y]←"↑";
Else If C[x,y-1]+a_y< C[x-1,y]+a_x
Then C[x,y]←C[x-1,y]+a_x;
B[x,y]←"←";
Return B and C;
Print-MTP(B,i,j)
If i=0 and j=0
Then Return;
If B[i,j]=="←"
Then Print-MTP(B,i-1,j);
Print "A[i,j]";
If B[i,j]=="↑"
Then Print-MTP(B,i,j-1);
Print "A[i,j]";
结果
以下图片表示从点(0,0)开始依次经过以下顺序的点到达终点(4,4)。总共经过9个点,8段路程,所经过的路径的权值总和是所有路径中最大的。

结果分析
矩阵A[i,j]为输入的测试数据,数值如下所示。这里要注意,行是j,列是i。

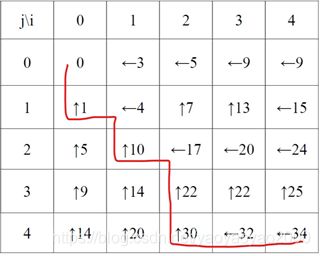
矩阵B[i,j],C[i,j]构造后如下所示

从点(0,0)到点(4,4)的路线如下图所示
设矩阵有n列,m行,根据递推公式和伪代码,可以推出函数Construct-MTP(A[i,j])的时间复杂度为T(n)=θ(n)+θ(m)+θ(mn)=θ(mn)。函数Print-MTP(B,i,j)的时间复杂度是T(n)=θ(n+m)。二者总体时间复杂性是T(n)=θ(mn)。
由于算法使用了三个二维数组来存储数据,所以,算法的空间复杂度是T(n)=θ(mn)+θ(mn)+θ(mn)=θ(mn)。
源代码
Point.java
public class Point {
private int x;
private int y;
public Point(int x, int y) {
super();
this.x = x;
this.y = y;
}
public int getX() {
return x;
}
public void setX(int x) {
this.x = x;
}
public int getY() {
return y;
}
public void setY(int y) {
this.y = y;
}
@Override
public String toString() {
return "x=" + x + ", y=" + y;
}
}
Main.java
public class Main {
private static Point[][] A;//距离数据
private static Point[][] getA() {
A[0][0] = new Point(0, 0);
A[0][1] = new Point(0, 1);
A[0][2] = new Point(0, 4);
A[0][3] = new Point(0, 4);
A[0][4] = new Point(0, 4);
A[1][0] = new Point(3, 0);
A[1][1] = new Point(3, 0);
A[1][2] = new Point(0, 6);
A[1][3] = new Point(3, 4);
A[1][4] = new Point(1, 6);
A[2][0] = new Point(2, 0);
A[2][1] = new Point(2, 2);
A[2][2] = new Point(7, 5);
A[2][3] = new Point(3, 5);
A[2][4] = new Point(3, 8);
A[3][0] = new Point(4, 0);
A[3][1] = new Point(4, 4);
A[3][2] = new Point(3, 2);
A[3][3] = new Point(0, 2);
A[3][4] = new Point(2, 5);
A[4][0] = new Point(0, 0);
A[4][1] = new Point(2, 3);
A[4][2] = new Point(4, 1);
A[4][3] = new Point(2, 1);
A[4][4] = new Point(2, 3);
return A;
}
private static int getI() {
return 5;
}
private static int getJ() {
return 5;
}
/**
* @param points A[i][j],到该点距离对
* @param i 列
* @param j 行
* @return B 箭头数组,用于构造解
*/
private static int[][] constructMTP(Point[][] points, int i, int j) {
//箭头数组
int[][] b = new int[i][j];
//结果数组
int[][] c = new int[i][j];
c[0][0] = 0;
for (int x = 1; x < i; x++) {
c[x][0] = c[x - 1][0] + points[x][0].getX();
b[x][0] = 0;//向左的箭头
}
for (int y = 1; y < j; y++) {
c[0][y] = c[0][y - 1] + points[0][y].getY();
b[0][y] = 1;//向上的箭头
}
for (int x = 1; x < i; x++) {
for (int y = 1; y < j; y++) {
if ((c[x][y - 1] + points[x][y].getY()) >= (c[x - 1][y] + points[x][y].getX())) {
c[x][y] = c[x][y - 1] + points[x][y].getY();
b[x][y] = 1;//向上的箭头
} else if ((c[x][y - 1] + points[x][y].getY()) < (c[x - 1][y] + points[x][y].getX())) {
c[x][y] = c[x - 1][y] + points[x][y].getX();
b[x][y] = 0;//向左的箭头
}
}
}
return b;
}
/**
* @param array B箭头数组,用于构造解
* @param i 列数
* @param j 行数
* @return 0:结束
*/
private static int printMTP(int[][] array, int i, int j) {
if (i == 0 && j == 0) {
System.out.println("[" + i + "," + j + "]");
return 0;
} else if (array[i][j] == 0) {
printMTP(array, i - 1, j);
System.out.println("[" + i + "," + j + "]");
} else if (array[i][j] == 1) {
printMTP(array, i, j - 1);
System.out.println("[" + i + "," + j + "]");
}
return 0;
}
public static void main(String[] args) {
A = new Point[getI()][getJ()];
int[][] i = constructMTP(getA(), getI(), getJ());
System.out.println(printMTP(i, getI() - 1, getJ() - 1));
}
}