机器学习——线性回归
机器学习——线性回归
- 线性回归
- 线性回归定义
- 最小二乘法之正规方程
- 最小二乘法之梯度下降法
- 回归性能评估
- 欠拟合与过拟合
- L2正则、L1正则与稀疏性
- 岭回归
- 模型拟合参数
- 波士顿房价案例数据分析
线性回归
线性回归定义
线性模型:试图学得一个通过属性的线性组合来进行预测的函数:
f ( x ) = w 1 x 1 + . . . + w n x n + b f(x)= w_1x_1+...+w_nx_n+b f(x)=w1x1+...+wnxn+b
w为权重,b为偏置项。
线性回归定义:线性回归通过一个或者多个自变量与因变量之间之间进行建模的回归分析。其中特点为一个或多个称为回归系数的模型参数的线性组合
一元线性回归:涉及到的变量只有一个
多元线性回归:涉及到的变量两个或两个以上
通用公式: h ( x ) = w 0 + w 1 x 1 + w 2 x 2 + . . . h(x)=w_0+w_1x_1+w_2x_2+... h(x)=w0+w1x1+w2x2+...
最小二乘法之正规方程
记 y i y_i yi 为第 i i i 个训练样本的真实值, h w ( x i ) h_w(x_i) hw(xi) 为第 i i i 个训练样本特征值组合预测函数,总损失定义为:
J ( θ ) = ( h w ( x 1 ) − y 1 ) 2 + ( h w ( x 2 ) − y 2 ) 2 + . . . + ( h w ( x m ) − y m ) 2 = ∑ i = 1 m ( h w ( x i ) − y i ) 2 J(\theta)=(h_w(x_1)-y_1)^2+(h_w(x_2)-y_2)^2+...+(h_w(x_m)-y_m)^2=\sum_{i=1}^{m}(h_w(x_i)-y_i)^2 J(θ)=(hw(x1)−y1)2+(hw(x2)−y2)2+...+(hw(xm)−ym)2=i=1∑m(hw(xi)−yi)2
最小二乘法:目的是找到最小损失对应的w值。
直接求解得到解为: w = ( X T X ) − 1 X y w = (X^TX)^{-1}Xy w=(XTX)−1Xy,为特征值矩阵,为目标值矩阵
-
缺点:
- 当特征过于复杂,求解速度太慢
- 对于复杂的算法,不能使用正规方程求解(逻辑回归等)
sklearn线性回归正规方程API: sklearn.linear_model.LinearRegression
-
sklearn.linear_model.LinearRegression()
- 普通最小二乘线性回归
- coef_:回归系数
最小二乘法之梯度下降法
思想:沿着这个函数下降的方向找,最后就能找到山谷的最低点,然后更新w值。
我们以单变量中的 w 0 , w 1 w_0,w_1 w0,w1为例子:
w 1 = w 1 − α ∂ c o s t ( w 0 + w 1 x 1 ) ∂ w 1 , w 0 = w 0 − α ∂ c o s t ( w 0 + w 1 x 1 ) ∂ w 1 w_1 = w_1-\alpha\frac{\partial cost(w_0+w_1x_1)}{\partial w_1},\ w_0 = w_0-\alpha\frac{\partial cost(w_0+w_1x_1)}{\partial w_1} w1=w1−α∂w1∂cost(w0+w1x1), w0=w0−α∂w1∂cost(w0+w1x1)
α \alpha α为学习速率,需要手动指定。
sklearn线性回归正规方程API: sklearn.linear_model.SGDRegressor()
- sklearn.linear_model.SGDRegressor()
- 通过使用SGD最小化线性模型
- coef_:回归系数
正规方程与梯度下降比较:
| 梯度下降 | 正规方程 |
|---|---|
| 需要选择学习率 α \alpha α | 不需要选择学习率 |
| 需要多次迭代 | 一次运算得出结果 |
| 当特征数量很大时也能较好适用 | 需要进行矩阵计算,如果特征值数量较大时运算代价太大,因为矩阵逆的计算时间复杂度为O( n 3 n^3 n3),通常来说当 n 小于10000时还是可以接受的 |
| 适用于各种类型的数据 | 只适用于线性模型,不适合逻辑回归模型等其他模型 |
注:线性回归算法需要对数据进行标准化!
回归性能评估
均方误差(MSE)评价机制:
M S E = 1 m ∑ i = 1 m ( y i − y i ˉ ) 2 MSE=\frac{1}{m}\sum_{i=1}^{m}(y_i-\bar{y_i})^2 MSE=m1i=1∑m(yi−yiˉ)2
其中 y i y_i yi为预测值, y i ˉ \bar{y_i} yiˉ为真实值。
sklearn回归评估API:sklearn.metrics.mean_squared_error
- mean_squared_error(y_true, y_pred)
- 均方误差回归损失
- y_true:真实值
- y_pred:预测值
- return:浮点数结果
注:真实值,预测值为标准化之前的值。
欠拟合与过拟合
过拟合:一个假设在训练数据上能够获得比其他假设更好的拟合, 但是在训练数据外的数据集上却不能很好地拟合数据,此时认为这个假设出现了过拟合的现象。(模型过于复杂)
欠拟合:一个假设在训练数据上不能获得更好的拟合, 但是在训练数据外的数据集上也不能很好地拟合数据,此时认为这个假设出现了欠拟合的现象。(模型过于简单)
- 欠拟合的原因及解决办法
- 原因:学习到数据的特征过少
- 解决办法:增加数据的特征数量
- 过拟合的原因及解决办法
- 原因:原始特征过多,存在一些嘈杂特征, 模型过于复杂是因为模型尝试去兼顾各个测试数据点
- 解决办法:
- 进行特征选择,消除关联性大的特征
- 正则化
L2正则、L1正则与稀疏性
线性回归的目标函数为:
J ( θ ) = 1 2 ∑ i = 1 m ( θ T x ( i ) − y ( i ) ) 2 , J(\theta)=\frac{1}{2}\sum_{i=1}^{m}(\theta^Tx^{(i)}-y^{(i)})^2, J(θ)=21i=1∑m(θTx(i)−y(i))2,
L2正则化
对上述目标函数增加一个平方和损失,目标函数变为:
J ( θ ) = 1 2 ∑ i = 1 m ( θ T x ( i ) − y ( i ) ) 2 + λ ∑ j = 1 n θ j 2 , J(\theta)=\frac{1}{2}\sum_{i=1}^{m}(\theta^Tx^{(i)}-y^{(i)})^2+\lambda\sum_{j=1}^{n}\theta_j^2, J(θ)=21i=1∑m(θTx(i)−y(i))2+λj=1∑nθj2,
可以防止过拟合现象。
原因:
将损失函数增加了系数造成的损失,可以防止系数过大,从而不会过拟合,因为过拟合的时候,拟合函数需要顾及每一个点,最终形成的拟合函数波动会非常大,在某些很小的区间内,函数值的变化会很剧烈,就意味着在某些很小区间内的导数值的绝对值会非常大,又由于自变量可大可小,所以只有系数足够大,才能保证导数值的绝对值足够大,因此过拟合的时候拟合函数系数往往非常大,而添加了正则项之后使得系数不会过大,因此不会发生过拟合现象。
此时最小二乘法的解为 ( X T X + λ I ) − 1 X T Y (X^TX+\lambda I)^{-1}X^TY (XTX+λI)−1XTY,又因为 X T X + λ I X^TX+\lambda I XTX+λI正定,所以可逆。
L1正则化
对上述目标函数增加一个绝对值损失,目标函数变为:
J ( θ ) = 1 2 ∑ i = 1 m ( θ T x ( i ) − y ( i ) ) 2 + λ ∑ j = 1 n ∣ θ j ∣ , J(\theta)=\frac{1}{2}\sum_{i=1}^{m}(\theta^Tx^{(i)}-y^{(i)})^2+\lambda\sum_{j=1}^{n}|\theta_j|, J(θ)=21i=1∑m(θTx(i)−y(i))2+λj=1∑n∣θj∣,
不仅可以防止过拟合,还具有特征选择的功能。
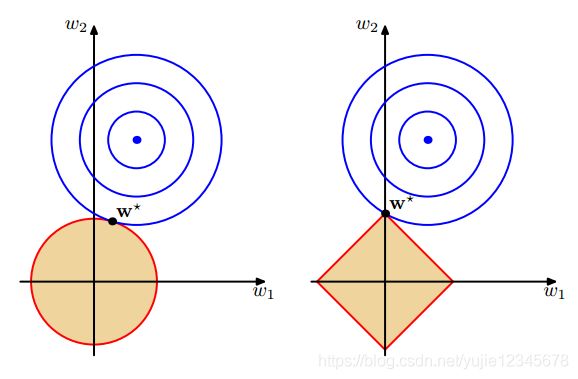
可以看出L1的交点是在轴上,因此必有特征的参数是趋近于0的,因此具有特征选择功能。
岭回归:带L2正则化的线性回归
LASSO回归:带L1正则化的线性回归
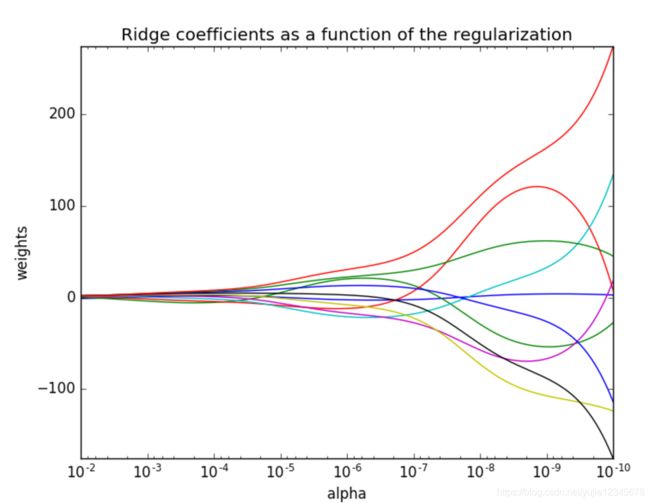
岭回归
带有正则化的线性回归-Ridge:sklearn.linear_model.Ridge
- sklearn.linear_model.Ridge( α \alpha α=1.0)
线性回归 LinearRegression与Ridge对比
岭回归:回归得到的回归系数更符合实际,更可靠。另外,能让估计参数的波动范围变小,变的更稳定。在存在病态数据偏多的研究中有较大的实用价值。
模型拟合参数
总平方和TSS(Total Sum of Squares): T S S = ∑ i = 1 m ( y i − y ˉ ) 2 TSS=\sum_{i=1}^{m}(y_i-\bar{y})^2 TSS=∑i=1m(yi−yˉ)2;
残差平方和RSS(Residual Sum of Squares): R S S = ∑ i = 1 m ( y i ^ − y i ) 2 RSS=\sum_{i=1}^{m}(\hat{y_i}-y_i)^2 RSS=∑i=1m(yi^−yi)2;
ESS(又称回归平方和SSR): E S S = ∑ i = 1 m ( y i ^ − y ˉ ) 2 ESS=\sum_{i=1}^{m}(\hat{y_i}-\bar{y})^2 ESS=∑i=1m(yi^−yˉ)2,在无偏估计时,TSS=ESS+RSS
定义 R 2 = 1 − R S S / T S S R^2=1-RSS/TSS R2=1−RSS/TSS,R^2越大代表拟合效果越好,最优值为1
波士顿房价案例数据分析
from sklearn.linear_model import LinearRegression
from sklearn.linear_model import SGDRegressor
from sklearn.linear_model import Ridge
from sklearn.datasets import load_boston
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.metrics import mean_squared_error
lb = load_boston()
# 分割数据集
x_train, x_test, y_train, y_test = train_test_split(lb.data, lb.target, test_size=0.25)
# 标准化
sd_x = StandardScaler()
x_train = sd_x.fit_transform(x_train)
x_test = sd_x.transform(x_test)
sd_y = StandardScaler()
y_train = sd_y.fit_transform(y_train.reshape(-1,1))
y_test = sd_y.transform(y_test.reshape(-1,1))
# 正规方程
lr = LinearRegression()
lr.fit(x_train, y_train)
# 求出权重
print(lr.coef_)
# 预测数值
y_lr_predict = sd_y.inverse_transform(lr.predict(x_test))
# 均方误差
print("正规方程的均方误差:", mean_squared_error(sd_y.inverse_transform(y_test), y_lr_predict))
# 梯度下降
sdg = SGDRegressor()
sdg.fit(x_train,y_train)
# 求出权重
print(sdg.coef_)
# 预测数值
y_sdg_predict = sd_y.inverse_transform(sdg.predict(x_test))
# 均方误差
print("正规方程的均方误差:", mean_squared_error(sd_y.inverse_transform(y_test), y_sdg_predict))
# 岭回归
rd = Ridge(alpha=1.0)
rd.fit(x_train,y_train)
# 求出权重
print(rd.coef_)
# 预测数值
y_rd_predict = sd_y.inverse_transform(rd.predict(x_test))
# 均方误差
print("正规方程的均方误差:", mean_squared_error(sd_y.inverse_transform(y_test), y_rd_predict))