【本文作者】达观数据 夏琦
【本文作者】达观数据 夏琦
【作者简介】夏琦,达观数据NLP组实习生,就读于东南大学和 Monash University,自然语言处理方向二年级研究生,师从知识图谱专家漆桂林教授。曾获第五届“蓝桥杯”江苏省一等奖、国家二等奖。
前言
本篇博文将详细讲解LDA主题模型,从最底层数学推导的角度来详细讲解,只想了解LDA的读者,可以只看第一小节简介即可。PLSA和LDA非常相似,PLSA也是主题模型方面非常重要的一个模型,本篇也会有的放矢的讲解此模型。如果读者阅读起来比较吃力,可以定义一个菲波那切数列,第 f(n) = f(n-1) + f(n-2) 天再阅读一次,直到这个知识点收敛。如果读者发现文章中的错误或者有改进之处,欢迎交流。
1. 简介
在机器学习领域,LDA是两个常用模型的简称:Linear Discriminant Analysis 和 Latent Dirichlet Allocation。本文的LDA仅指代Latent Dirichlet Allocation. LDA 在主题模型中占有非常重要的地位,常用来文本分类。
LDA由Blei, David M.、Ng, Andrew Y.、Jordan于2003年提出,用来推测文档的主题分布。它可以将文档集中每篇文档的主题以概率分布的形式给出,从而通过分析一些文档抽取出它们的主题分布后,便可以根据主题分布进行主题聚类或文本分类。
2. 先验知识
LDA 模型涉及很多数学知识,这也许是LDA晦涩难懂的主要原因。本小节主要介绍LDA中涉及的数学知识。数学功底比较好的同学可以直接跳过本小节。
LDA涉及到的先验知识有:二项分布、Gamma函数、Beta分布、多项分布、Dirichlet分布、马尔科夫链、MCMC、Gibs Sampling、EM算法等。限于篇幅,本文仅会有的放矢的介绍部分概念,不会每个概念都仔细介绍,亦不会涉及到每个概念的数学公式推导。如果每个概念都详细介绍,估计都可以写一本百页的书了。如果你对LDA的理解能达到如数家珍、信手拈来的程度,那么恭喜你已经掌握了从事机器学习方面的扎实数学基础。想进一步了解底层的数学公式推导过程,可以参考《数学全书》等资料。
2.1 词袋模型
LDA 采用词袋模型。所谓词袋模型,是将一篇文档,我们仅考虑一个词汇是否出现,而不考虑其出现的顺序。在词袋模型中,“我喜欢你”和“你喜欢我”是等价的。与词袋模型相反的一个模型是n-gram,n-gram考虑了词汇出现的先后顺序。有兴趣的读者可以参考其他书籍。
2.2 二项分布
二项分布是N重伯努利分布,即为X ~ B(n, p). 概率密度公式为:
$$ P(K = k) = \begin{pmatrix} n\\ k\\ \end{pmatrix}p^k{(1-p)}^{n-k} $$
2.3 多项分布
多项分布,是二项分布扩展到多维的情况. 多项分布是指单次试验中的随机变量的取值不再是0-1的,而是有多种离散值可能(1,2,3...,k).概率密度函数为:
$$ P(x_1, x_2, ..., x_k; n, p_1, p_2, ..., p_k) = \frac{n!}{x_1!...x_k!}{p_1}^{x_1}...{p_k}^{x_k} $$
2.4 Gamma函数
Gamma函数的定义:
$$ \Gamma(x) = \int_0^\infty t^{x-1}e^{-t}dt $$
分部积分后,可以发现Gamma函数如有这样的性质:
$$ \Gamma(x+1) = x\Gamma(x) $$
Gamma函数可以看成是阶乘在实数集上的延拓,具有如下性质:
$$ \Gamma(n) = (n-1)! $$
2.5 Beta分布
Beta分布的定义:对于参数alpha > 0, beta > 0, 取值范围为[0, 1]的随机变量x的概率密度函数为:
$$ \begin{align} f(x; \alpha, \beta) = \frac{1}{B(\alpha, \beta)} x^{\alpha - 1} {(1-x)}^{\beta-1} \end{align} $$
其中,
$$ \begin{align} \frac{1}{B(\alpha, \beta)} = \frac{\Gamma(\alpha + \beta)}{\Gamma(\alpha)\Gamma(\beta)} \end{align} $$
2.6 共轭先验分布
在贝叶斯概率理论中,如果后验概率P(θ|x)和先验概率p(θ)满足同样的分布律,那么,先验分布和后验分布被叫做共轭分布,同时,先验分布叫做似然函数的共轭先验分布。
$$ \begin{align} P(\theta | x) = \frac{P(\theta, x)} {P(x)} \end{align} $$
Beta分布是二项式分布的共轭先验分布,而狄利克雷(Dirichlet)分布是多项式分布的共轭分布。
共轭的意思是,以Beta分布和二项式分布为例,数据符合二项分布的时候,参数的先验分布和后验分布都能保持Beta分布的形式,这种形式不变的好处是,我们能够在先验分布中赋予参数很明确的物理意义,这个物理意义可以延续到后续分布中进行解释,同时从先验变换到后验过程中从数据中补充的知识也容易有物理解释。
2.7 Dirichlet分布
Dirichlet的概率密度函数为:
$$ \begin{align} f(x_1, x_2, ..., x_k; \alpha_1, \alpha_2, ..., \alpha_k) = \frac{1}{B(\alpha)}\prod_{i=1}^{k}{x_i}^{\alpha^i-1} \end{align} $$
其中,
$$ \begin{align} B(\alpha) = \frac{\prod_{i=1}^{k}\Gamma(\alpha^i)}{\Gamma(\sum_{i=1}^{k}\alpha^i)}, \sum_{i=1}^{k}x^i = 1 \end{align} $$
根据Beta分布、二项分布、Dirichlet分布、多项式分布的公式,我们可以验证上一小节中的结论 -- Beta分布是二项式分布的共轭先验分布,而狄利克雷(Dirichlet)分布是多项式分布的共轭分布。
2.8 Beta / Dirichlet 分布的一个性质
如果 $p ~ Beta(t | \alpha, \beta)$,则
$$ \begin{align} E(p) & = \int_0^1 t * Beta(t| \alpha, \beta)dt \\ & = \int_0^1 t * \frac{\Gamma(\alpha + \beta)}{\Gamma(\alpha)\Gamma(\beta)}t ^ {(\alpha -1)} {(1 - t)}^{\beta - 1}dt \\ & = \frac{\Gamma(\alpha + \beta)}{\Gamma(\alpha)\Gamma(\beta)}\int_0^1 t ^ \alpha {(1 - t)}^{\beta - 1}dt \end{align} $$
上式右边的积分对应到概率分布$Beta(t | \alpha + 1, \beta)$, 对于这个分布,有
$$ \int_0^1 \frac{\Gamma(\alpha + \beta + 1)}{\Gamma(\alpha + 1)\Gamma(\beta)}t^\alpha {(1-t)}^{\beta - 1}dt = 1 $$
把上式带入E(p)的计算式,得到
$$ \begin{align} E(p) & = \frac{\Gamma(\alpha + \beta)}{\Gamma(\alpha)\Gamma(\beta)} \cdot \frac{\Gamma(\alpha + 1)\Gamma(\beta)}{\Gamma(\alpha + \beta + 1)} \\ & = \frac{\Gamma(\alpha + \beta)}{\Gamma(\alpha + \beta + 1)} \cdot \frac{\Gamma(\alpha + 1)} {\Gamma(\alpha)} \\ & = \frac{\alpha}{\alpha + \beta} \end{align} $$
这说明,对于对于Beta分布的随机变量,其均值可以用$\frac{\alpha}{\alpha + \beta}$来估计。Dirichlet分布也有类似的结论,如果$\vec p \sim Dir (\vec t | \vec \alpha)$, 同样可以证明:
$$ \begin{align} E(p) & =\biggl ( \frac{\alpha ^ 1}{\sum_{i = 1}^K \alpha_i}, \frac{\alpha ^ 1}{\sum_{i = 2}^K \alpha_i}, \cdots, \frac{\alpha ^ K}{\sum_{i = 1}^K \alpha_i} \biggr) \end{align} $$
这两个结论非常重要,后面的LDA数学推导过程会使用这个结论。
2.9 MCMC 和 Gibbs Sampling
在现实应用中,我们很多时候很难精确求出精确的概率分布,常常采用近似推断方法。近似推断方法大致可分为两大类:第一类是采样(Sampling), 通过使用随机化方法完成近似;第二类是使用确定性近似完成近似推断,典型代表为变分推断(variational inference).
在很多任务中,我们关心某些概率分布并非因为对这些概率分布本身感兴趣,而是要基于他们计算某些期望,并且还可能进一步基于这些期望做出决策。采样法正式基于这个思路。具体来说,嘉定我们的目标是计算函数f(x)在概率密度函数p(x)下的期望
$$ \begin{align} E_p[f] & = \int f(x)p(x)dx \end{align} $$
则可根据p(x)抽取一组样本${x_1, x_2, \cdots, x_N}$,然后计算f(x)在这些样本上的均值
$$ \begin{align} \hat f & = \frac{1}{N} \sum_{i=1}^Nf(x_i) \end{align} $$
以此来近似目标期望E[f]。若样本${x_1, x_2, \cdots, x_N}$独立,基于大数定律,这种通过大量采样的办法就能获得较高的近似精度。可是,问题的关键是如何采样?对概率图模型来说,就是如何高效地基于图模型所描述的概率分布来获取样本。概率图模型中最常用的采样技术是马尔可夫链脸蒙特卡罗(Markov chain Monte Carlo, MCMC). 给定连续变量$x \in X$的概率密度函数p(x), x在区间A中的概率可计算为
$$ \begin{align} P(A) & = \int_A p(x)dx \end{align} $$
若有函数$f: X \mapsto R$, 则可计算f(x)的期望
$$ \begin{align} P(f) & = E_p[f(X)] = \int_x f(x)p(x)dx \end{align} $$
若x不是单变量而是一个高维多元变量x, 且服从一个非常复杂的分布,则对上式求积分通常很困难。为此,MCMC先构造出服从p分布的独立同分布随机变量$x_1, x_2, \cdots, x_N$, 再得到上式的无偏估计
$$ \begin{align} \tilde p(f) & = \frac{1}{N}\sum_{i=1}^Nf(xi) \end{align} $$
然而,若概率密度函数p(x)很复杂,则构造服从p分布的独立同分布样本也很困难。MCMC方法的关键在于通过构造“平稳分布为p的马尔可夫链”来产生样本:若马尔科夫链运行时间足够长,即收敛到平稳状态,则此时产出的样本X近似服从分布p.如何判断马尔科夫链到达平稳状态呢?假定平稳马尔科夫链T的状态转移概率(即从状态X转移到状态$x^{'}$的概率)为$T(x^{'} \mid x)$, t时刻状态的分布为p(x^t), 则若在某个时刻马尔科夫链满足平稳条件
$$ \begin{align} p(x^t)T(x^{t-1} \mid x^t) = p(x^{t-1})T(x^t \mid x^{t-1}) \end{align} $$
则p(x)是马尔科夫链的平稳分布,且马尔科夫链在满足该条件时已收敛到平稳条件。也就是说,MCMC方法先设法构造一条马尔科夫链,使其收敛至平稳分布恰为待估计参数的后验分布,然后通过这条马尔科夫链来产生符合后验分布的样本,并基于这些样本来进行估计。这里马尔科夫链转移概率的构造至关重要,不同的构造方法将产生不同的MCMC算法。
Metropolis-Hastings(简称MH)算法是MCMC的重要代表。它基于“拒绝采样”(reject sampling)来逼近平稳分布p。算法如下:
- 输入:先验概率$Q(x^{\ast} \mid x^{t-1})$
- 过程:
- 1. 初始化x^0;
- 2. for t = 1, 2, ... do
- 3. 根据$Q(x^{\ast} \mid x^{t-1})$采样出候选样本$x^{\ast}$
- 4. 根据均匀分布从(0, 1)范围内采样出阈值u;
- 5. if u $\le A(x^{\ast} \mid x^{t-1}) then$
- 6. $x^t = x^{\ast}$
- 7. else
- 8. $x^t = x^{t-1}$
- 9. end if
- 10. enf for
- 11. return $x^1, x^2, ...$
- 输出:采样出的一个样本序列$x^1, x^2, ...$
于是, 为了达到平稳状态,只需将接受率设置为
$$ \begin{align} A(x^{\ast} \mid x^{t-1}) = min \biggl( 1, \frac{p(x^{\ast}Q(x^{t-1} \mid x^{\ast}))}{p(x^{t-1})Q(x^{\ast} \mid x^{t-1})}\biggr) \end{align} $$
吉布斯采样(Gibbs sampling)有时被视为MH算法的特例,它也使用马尔科夫链读取样本,而该马尔科夫链的平稳分布也是采用采样的目标分布p(x).具体来说,假定$x = {x_1, x_2, \cdots, x_N}$, 目标分布为p(x), 在初始化x的取值后,通过循环执行以下步骤来完成采样:
- 1. 随机或以某个次序选取某变量$x_i$ ;
- 2. 根据x中除$x_i$外的变量的现有取值,计算条件概率$p(x_i \mid X_i)$, 其中$X_i = {x_1, x_2, \cdots, x_{i-1}, x_{i+1}, \cdots, x_N}$ ;
- 3. 根据$p(x_i \mid X_i)$对变量$x_i$采样,用采样值代替原值.
3. 文本建模
一篇文档,可以看成是一组有序的词的序列$d = (\omega_1, \omega_2, \cdots, \omega_n)$. 从统计学角度来看,文档的生成可以看成是上帝抛掷骰子生成的结果,每一次抛掷骰子都生成一个词汇,抛掷N词生成一篇文档。在统计文本建模中,我们希望猜测出上帝是如何玩这个游戏的,这会涉及到两个最核心的问题:
- 上帝都有什么样的骰子;
- 上帝是如何抛掷这些骰子的;
第一个问题就是表示模型中都有哪些参数,骰子的每一个面的概率都对应于模型中的参数;第二个问题就表示游戏规则是什么,上帝可能有各种不同类型的骰子,上帝可以按照一定的规则抛掷这些骰子从而产生词序列。
3.1 Unigram Model
在Unigram Model中,我们采用词袋模型,假设了文档之间相互独立,文档中的词汇之间相互独立。假设我们的词典中一共有 V 个词 $\nu_1, \nu_2, \cdots, \nu_V$,那么最简单的 Unigram Model 就是认为上帝是按照如下的游戏规则产生文本的。
- 1. 上帝只有一个骰子,这个骰子有V面,每个面对应一个词,各个面的概率不一;
- 2. 每抛掷一次骰子,抛出的面就对应的产生一个词;如果一篇文档中N个词,就独立的抛掷n次骰子产生n个词;
3.1.1 频率派视角
对于一个骰子,记各个面的概率为$\vec p = (p_1, p_2, \cdots, p_V)$, 每生成一个词汇都可以看做一次多项式分布,记为$\omega \sim Mult(\omega \mid \vec p)$。一篇文档$d = \vec \omega = (\omega_1, \omega_2, \cdots, \omega_n)$, 其生成概率是
$$ p(\vec \omega) = p (\omega_1, \omega_2, \cdots, \omega_n) = p(\omega_1)p(\omega_2) \cdots p(\omega_n) $$
文档之间,我们认为是独立的,对于一个语料库,其概率为:$W = (\vec \omega_1, \vec \omega_2, \cdots, \vec \omega_m)$。
假设语料中总的词频是N,记每个词$\omega_i$的频率为$n_i$, 那么$\vec n = (n_1, n_2, \cdots, n_V)$, $\vec n$服从多项式分布
$$ p(\vec n) = Mult(\vec n \mid \vec p, N) = \begin{pmatrix} N \\ \vec n \end{pmatrix} \prod_{k = 1}^V p_k^{n_k} $$
整个语料库的概率为
$$ p(W) = p(\vec \omega_1) p(\vec \omega_2) \cdots p(\vec \omega_m) = \prod_{k = 1}^V p_k^{n_k} $$
此时,我们需要估计模型中的参数$\vec p$,也就是词汇骰子中每个面的概率是多大,按照频率派的观点,使用极大似然估计最大化p(W), 于是参数$p_i$的估计值为
$$ \hat p_i = \frac{n_i}{N} $$
3.1.2 贝叶斯派视角
对于以上模型,贝叶斯统计学派的统计学家会有不同意见,他们会很挑剔的批评只假设上帝拥有唯一一个固定的骰子是不合理的。在贝叶斯学派看来,一切参数都是随机变量,以上模型中的骰子 $\vec p$不是唯一固定的,它也是一个随机变量。所以按照贝叶斯学派的观点,上帝是按照以下的过程在玩游戏的:
- 1. 现有一个装有无穷多个骰子的坛子,里面装有各式各样的骰子,每个骰子有V个面;
- 2. 现从坛子中抽取一个骰子出来,然后使用这个骰子不断抛掷,直到产生语料库中的所有词汇
坛子中的骰子无限多,有些类型的骰子数量多,有些少。从概率分布角度看,坛子里面的骰子$\vec p$服从一个概率分布$p(\vec p)$, 这个分布称为参数$\vec p$的先验分布。在此视角下,我们并不知道到底用了哪个骰子$\vec p$,每个骰子都可能被使用,其概率由先验分布$p(\vec p)$来决定。对每个具体的骰子,由该骰子产生语料库的概率为$p(W \mid \vec p)$, 故产生语料库的概率就是对每一个骰子$\vec p$上产生语料库进行积分求和
$$ p(W) = \int p(W \mid \vec p) p(\vec p) d \vec p $$
先验概率有很多选择,但我们注意到$p(\vec n) = Mult(\vec n \mid \vec p, N)$. 我们知道多项式分布和狄利克雷分布是共轭分布,因此一个比较好的选择是采用狄利克雷分布
$$ Dir(\vec p \mid \vec \alpha) = \frac{1}{\Delta (\vec \alpha)} \prod_{k=1}^Vp_k^{\alpha_k -1}, \vec \alpha = (\alpha_1, \cdots, \alpha_V) $$
此处,$\Delta(\vec \alpha)就是归一化因子Dir(\vec \alpha)$, 即
$$ \Delta(\vec \alpha) = \int \prod_{k=1}^Vp_k^{\alpha_k - 1}d\vec p $$
由多项式分布和狄利克雷分布是共轭分布,可得:
$$ \begin{align} p(\vec p | W, \vec \alpha) = Dir(\vec p \mid \vec n + \vec \alpha) = \frac{1}{\Delta(\vec n + \vec \alpha)} \prod_{k = 1}^V p_k^{n_k + \alpha_k - 1}d\vec p \end{align} $$
此时,我们如何估计参数$\vec p$呢?根据上式,我们已经知道了其后验分布,所以合理的方式是使用后验分布的极大值点,或者是参数在后验分布下的平均值。这里,我们取平均值作为参数的估计值。根据第二小节Dirichlet分布中的内容,可以得到:
$$ \begin{align} E(\vec p) = \biggl( \frac{n_1 + \alpha_1}{\sum_{i=1}^V (n_i + \alpha_i)}, \frac{n_2 + \alpha_2}{\sum_{i=1}^V (n_i + \alpha_i)}, \cdots, \frac{n_V + \alpha_V}{\sum_{i=1}^V (n_i + \alpha_i)} \biggr) \end{align} $$
对于每一个$p_i$, 我们使用下面的式子进行估计
$$ \begin{align} \hat p_i = \frac{n_i + \alpha_i}{\sum_{i=1}^V(n_i + \alpha_i)} \end{align} $$
$\alpha_i$在 Dirichlet 分布中的物理意义是事件的先验的伪计数,上式表达的是:每个参数的估计值是其对应事件的先验的伪计数和数据中的计数的和在整体计数中的比例。由此,我们可以计算出产生语料库的概率为:
$$ \begin{align} p(W \mid \alpha) & = \int p(W \mid \alpha) p(\vec p \mid \alpha)d\vec p \\ & = \int \prod_{k=1}^V p_k^{n_k}Dir(\vec p \mid \vec \alpha)d\vec p \\ & = \int \prod_{k=1}^V p_k^{n_k} \frac{1}{\Delta(\vec \alpha)} \prod_{k = 1}^V p_k^{\alpha_k - 1}d\vec p \\ & = \frac{1}{\Delta(\vec \alpha)} \int \prod_{k=1}^V p_k^{n_k} \prod_{k = 1}^V p_k^{n_k + \alpha_k - 1}d\vec p \\ & = \frac{\Delta(\vec n + \vec \alpha)}{\Delta(\vec \alpha)} \end{align} $$
3.2 PLSA模型
Unigram Model模型中,没有考虑主题词这个概念。我们人写文章时,写的文章都是关于某一个主题的,不是满天胡乱的写,比如一个财经记者写一篇报道,那么这篇文章大部分都是关于财经主题的,当然,也有很少一部分词汇会涉及到其他主题。所以,PLSA认为生成一篇文档的生成过程如下:
- 1. 现有两种类型的骰子,一种是doc-topic骰子,每个doc-topic骰子有K个面,每个面一个topic的编号;一种是topic-word骰子,每个topic-word骰子有V个面,每个面对应一个词;
- 2. 现有K个topic-word骰子,每个骰子有一个编号,编号从1到K;
- 3. 生成每篇文档之前,先为这篇文章制造一个特定的doc-topic骰子,重复如下过程生成文档中的词:
- 3.1 投掷这个doc-topic骰子,得到一个topic编号z;
- 3.2 选择K个topic-word骰子中编号为z的那个,投掷这个骰子,得到一个词;
PLSA中,也是采用词袋模型,文档和文档之间是独立可交换的,同一个文档内的词也是独立可交换的。K 个topic-word 骰子,记为$\vec \phi_1, \cdots, \vec \phi_K$; 对于包含M篇文档的语料 $C = (d_1,d_2, \cdots,d_M) $中的每篇文档$d_m$,都会有一个特定的doc-topic骰子$\vec \theta_m$,所有对应的骰子记为 $\vec \theta_1, \cdots, \vec \theta_M$。为了方便,我们假设每个词$\omega$都有一个编号,对应到topic-word 骰子的面。于是在 PLSA 这个模型中,第m篇文档 $d_m$ 中的每个词的生成概率为
$$ \begin{align} p(\omega \mid d_m) & = \sum_{z=1}^K p(\omega \mid z) p(z \mid d_m) \\ & = \sum_{z = 1}^K \phi_{z \omega} \theta_{\omega z} \end{align} $$
一篇文档的生成概率为:
$$ \begin{align} p(\vec \omega \mid d_m) & = \prod_{i = 1}^n \sum_{z=1}^K p(\omega \mid z) p(z \mid d_m) \\ & = \prod_{i = 1}^n \sum_{z = 1}^K \phi_{z \omega} \theta_{\omega z} \end{align} $$
由于文档之间相互独立,很容易写出整个语料的生成概率。求解PLSA 可以使用著名的 EM 算法进行求得局部最优解,有兴趣的同学参考 Hoffman 的原始论文,或者李航的《统计学习方法》,此处略去不讲。
3.3 LDA 模型
3.3.1 PLSA 和 LDA 的区别
首先,我们来看看PLSA和LDA生成文档的方式。在PLSA中,生成文档的方式如下:
- 1. 按照概率$p(d_i)$选择一篇文档$d_i$
- 2. 根据选择的文档$d_i$,从从主题分布中按照概率$p(\zeta_k \mid d_i)$选择一个隐含的主题类别$\zeta_k$
- 3. 根据选择的主题$\zeta_k$, 从词分布中按照概率$p(\omega_j \mid \zeta_k)$选择一个词$\omega_j$
LDA 中,生成文档的过程如下:
- 1. 按照先验概率$p(d_i)$选择一篇文档$d_i$
- 2. 从Dirichlet分布$\alpha$中取样生成文档$d_i$的主题分布$\theta_i$,主题分布$\theta_i$由超参数为$\alpha$的Dirichlet分布生成
- 3. 从主题的多项式分布$\theta_i$中取样生成文档$d_i$第 j 个词的主题$z_{i, j}$
- 4. 从Dirichlet分布$\beta$中取样生成主题$z_{i, j}$对应的词语分布$\phi_{z_{i, j}}$,词语分布$\phi_{z_{i, j}}$由参数为$\beta$的Dirichlet分布生成
- 5. 从词语的多项式分布$\phi_{z_{i, j}}$中采样最终生成词语$\omega_{i, j}$
可以看出,LDA 在 PLSA 的基础上,为主题分布和词分布分别加了两个 Dirichlet 先验。
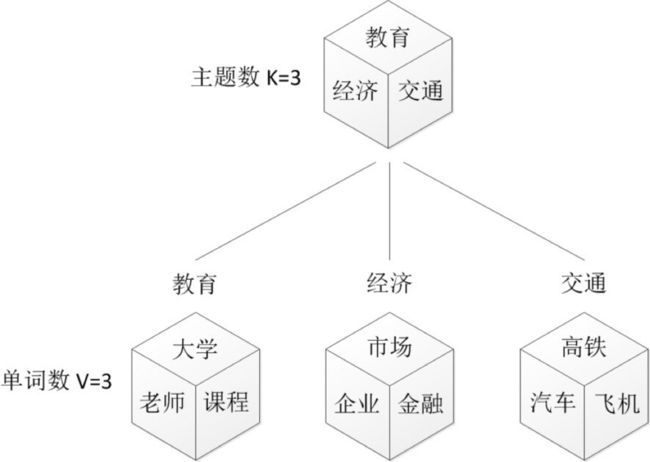
我们来看一个例子,如图所示:
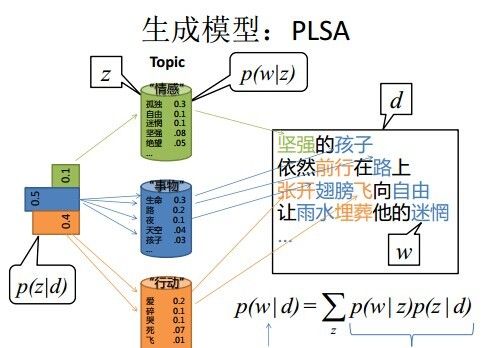
上图中有三个主题,在PLSA中,我们会以固定的概率来抽取一个主题词,比如0.5的概率抽取教育这个主题词,然后根据抽取出来的主题词,找其对应的词分布,再根据词分布,抽取一个词汇。由此,可以看出PLSA中,主题分布和词分布都是唯一确定的。但是,在LDA中,主题分布和词分布是不确定的,LDA的作者们采用的是贝叶斯派的思想,认为它们应该服从一个分布,主题分布和词分布都是多项式分布,因为多项式分布和狄利克雷分布是共轭结构,在LDA中主题分布和词分布使用了Dirichlet分布作为它们的共轭先验分布。所以,也就有了一句广为流传的话 -- LDA 就是 PLSA 的贝叶斯化版本。下面两张图片很好的体现了两者的区别:
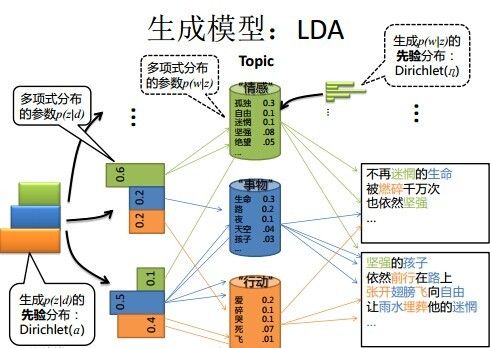
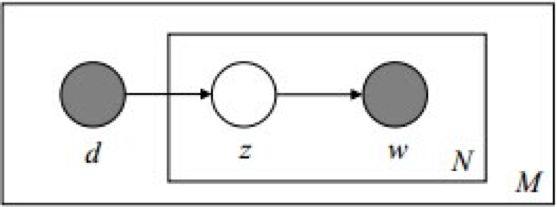
在PLSA和LDA的两篇论文中,使用了下面的图片来解释模型,它们也很好的对比了PLSA和LDA的不同之处。
3.3.2 LDA 解析一
现在我们来详细讲解论文中的LDA模型,即上图。
$\vec \alpha \to \vec \theta_m \to \zeta_{m, n}$, 这个过程表示在生成第m篇文档的时候,先从抽取了一个doc-topic骰子$\vec \theta_m$, 然后投掷这个骰子生成了文档中第n个词的topic编号$\zeta_{m, n}$;
$\vec \beta \to \vec \phi_k \to \omega_{m, n}\mid = \zeta_{m ,n}$, 这个过程表示,从K个topic-word骰子$\vec \phi_k$中,挑选编号为$k = \zeta_{m, n}$的骰子进行投掷,然后生成词汇$\omega_{m , n}$;
在LDA中,也是采用词袋模型,M篇文档会对应M个独立Dirichlet-Multinomial共轭结构;K个topic会对应K个独立的Dirichlet-Multinomial共轭结构。
3.3.3 LDA 解析二
上面的LDA的处理过程是一篇文档一篇文档的过程来处理,并不是实际的处理过程。文档中每个词的生成都要抛两次骰子,第一次抛一个doc-topic骰子得到 topic, 第二次抛一个topic-word骰子得到 word,每次生成每篇文档中的一个词的时候这两次抛骰子的动作是紧邻轮换进行的。如果语料中一共有 N 个词,则上帝一共要抛 2N次骰子,轮换的抛doc-topic骰子和 topic-word骰子。但实际上有一些抛骰子的顺序是可以交换的,我们可以等价的调整2N次抛骰子的次序:前N次只抛doc-topic骰子得到语料中所有词的 topics,然后基于得到的每个词的 topic 编号,后N次只抛topic-word骰子生成 N 个word。此时,可以得到:
$$ \begin{align} p(\vec w , \vec z \mid \vec \alpha, \vec \beta) & = p(\vec w \mid \vec z, \vec \beta) p(\vec z \mid \vec \alpha) \\ & = \prod_{k=1}^K\frac{\Delta(\vec \phi_K + \vec \beta)}{\Delta (\vec \beta)} \prod_{m=1}^M \frac{\Delta(\vec \theta_m + \vec \alpha)}{\vec \alpha} \end{align} $$
3.3.4 使用Gibbs Sampling进行采样
根据上一小节中的联合概率分布$p(\vec \omega, \vec z)$, 我们可以使用Gibbs Sampling对其进行采样。
语料库$\vec z$中的第i个词我们记为$z_i$, 其中i=(m,n)是一个二维下标,对应于第m篇文档的第n个词,用$\lnot i$ 表示去除下标为i的词。根据第二小节中的Gibbs Sampling 算法,我们需要求任一个坐标轴 i 对应的条件分布 $p(z_i=k|\vec z_{\lnot i}, \vec \omega)$ 。假设已经观测到的词 $\omega_i=t$, 则由贝叶斯法则,我们容易得到:
$$ \begin{align} p(z_i = k \mid \vec z_{\lnot i}, \vec \omega) & ∝ p(z_i = k, \omega_i = t \mid \vec z_{\lnot i}, \vec \omega_{\lnot i}) \end{align} $$
由于$z_i=k,w_i=t$ 只涉及到第 m 篇文档和第k个 topic,所以上式的条件概率计算中, 实际上也只会涉及到与之相关的两个Dirichlet-Multinomial 共轭结构,其它的 M+K−2 个 Dirichlet-Multinomial 共轭结构和$z_i=k,w_i=t$是独立的。去掉一个词汇,并不会改变M + K 个Dirichlet-Multinomial共轭结构,只是某些地方的计数减少而已。于是有:
$$ \begin{align} p(\vec \theta_m \mid \vec z_{\lnot i}, \vec \omega_{\lnot i}) & = Dir(\vec \theta_m \mid \vec n_{m, \lnot i} + \vec \alpha) \\ p(\vec \varphi_k \mid \vec z_{\lnot i}, \vec \omega_{\lnot i}) & = Dir(\vec \varphi_k \mid \vec n_{k, \lnot i} + \vec \beta) \end{align} $$
下面进行本篇文章最终的核心数学公式推导:
$$ \begin{align} p(z_i = k \mid \vec z_{\lnot i}, \vec \omega) & \propto p(z_i = k, \omega_i = t \mid \vec z_{\lnot i}, \vec \omega_{\lnot i}) \\ & = \int p(z_i = k, \omega_i = t, \vec \theta_m, \vec \varphi_k \mid \vec z_{\lnot i}, \vec \omega_{\lnot i})d\vec \theta_m d \vec \varphi_k \\ & = \int p(z_i = k, \vec \theta_m, \mid \vec z_{\lnot i}, \vec \omega_{\lnot i}) \cdot p(\omega_i = t, \vec \varphi_k, \mid \vec z_{\lnot i}, \vec \omega_{\lnot i}) d\vec \theta_m d \vec \varphi_k \\ & = \int p(z_i = k \mid \vec \theta_m) p(\vec \theta_m \mid \vec z_{\lnot i}, \vec \omega_{\lnot i}) \cdot p(\omega_i = t \mid \vec \varphi_k)p(\vec \varphi_k \mid \vec z_{\lnot i}, \vec \omega_{\lnot i}) d\vec \theta_m d \vec \varphi_k \\ & = \int p(z_i = k \mid \vec \theta_m) Dir(\vec \theta_m \mid \vec n_{m, \lnot i} + \vec \alpha) d \vec \theta_m \cdot p(\omega_i = t \mid \vec \varphi_k) Dir(\vec \varphi_k \mid \vec n_{k, \lnot i} + \vec \beta) d \vec \varphi_k \\ & = \int \theta_{mk} Dir(\vec \theta_m \mid \vec n_{m, \lnot i} + \vec \alpha) d \vec \theta_m \cdot \int \varphi_{kt} Dir(\vec \varphi_k \mid \vec n_{k, \lnot i} + \vec \beta) d \vec \varphi_k \\ & = E(\theta_{mk}) \cdot E(\varphi_{kt}) \\ & = \hat \theta_{mk} \cdot \hat \varphi_{kt} \end{align} $$
最终得到的 $\hat \theta_{mk} \cdot \hat \varphi_{kt}$ 就是对应的两个 Dirichlet 后验分布在贝叶斯框架下的参数估计。借助于前面介绍的Dirichlet 参数估计的公式 ,有:
$$ \begin{align} \hat{\theta}_{mk} &= \frac{n_{m,\neg i}^{(k)} + \alpha_k}{\sum_{k=1}^K (n_{m,\neg i}^{(k)} + \alpha_k)} \\ \hat{\varphi}_{kt} &= \frac{n_{k,\neg i}^{(t)} + \beta_t}{\sum_{t=1}^V (n_{k,\neg i}^{(t)} + \beta_t)} \end{align} $$
最终,我们得到LDA 模型的 Gibbs Sampling 公式为:
$$ \begin{align} p(z_i = k|\overrightarrow{\mathbf{z}}_{\neg i}, \overrightarrow{\mathbf{w}}) \propto \frac{n_{m,\neg i}^{(k)} + \alpha_k}{\sum_{k=1}^K (n_{m,\neg i}^{(k)} + \alpha_k)} \cdot \frac{n_{k,\neg i}^{(t)} + \beta_t}{\sum_{t=1}^V (n_{k,\neg i}^{(t)} + \beta_t)} \end{align} $$
3.3.5 LDA Training
根据上一小节中的公式,我们的目标有两个:
- 1. 估计模型中的参数 $\vec \varphi_1, \cdots, \vec \varphi_K$ 和 $\theta_1, \cdots, \theta_M$;
- 2. 对于新来的一篇文档,我们能够计算这篇文档的 topic 分布$\vec \theta$。
训练的过程:
- 1. 对语料库中的每篇文档中的每个词汇$\omega$,随机的赋予一个topic编号z
- 2. 重新扫描语料库,对每个词$\omega$,使用Gibbs Sampling公式对其采样,求出它的topic,在语料中更新
- 3. 重复步骤2,直到Gibbs Sampling收敛
- 4. 统计语料库的topic-word共现频率矩阵,该矩阵就是LDA的模型;
根据这个topic-word频率矩阵,我们可以计算每一个p(word|topic)概率,从而算出模型参数$\vec \varphi_1, \cdots, \vec \varphi_K$, 这就是那 K 个 topic-word 骰子。而语料库中的文档对应的骰子参数 $\theta_1, \cdots, \theta_M$ 在以上训练过程中也是可以计算出来的,只要在 Gibbs Sampling 收敛之后,统计每篇文档中的 topic 的频率分布,我们就可以计算每一个 p(topic|doc) 概率,于是就可以计算出每一个$\theta_m$。由于参数$\theta_m$ 是和训练语料中的每篇文档相关的,对于我们理解新的文档并无用处,所以工程上最终存储 LDA 模型时候一般没有必要保留。通常,在 LDA 模型训练的过程中,我们是取 Gibbs Sampling 收敛之后的 n 个迭代的结果进行平均来做参数估计,这样模型质量更高。
3.3.6 LDA Inference
有了 LDA 的模型,对于新来的文档 doc, 我们只要认为 Gibbs Sampling 公式中的 $\vec \varphi_{kt}$ 部分是稳定不变的,是由训练语料得到的模型提供的,所以采样过程中我们只要估计该文档的 topic 分布$\theta$就好了. 具体算法如下:
- 1. 对当前文档中的每个单词$\omega$, 随机初始化一个topic编号z;
- 2. 使用Gibbs Sampling公式,对每个词$\omega$, 重新采样其topic;
- 3. 重复以上过程,知道Gibbs Sampling收敛;
- 4. 统计文档中的topic分布,该分布就是$\vec \theta$
4 Tips
懂 LDA 的面试官通常会询问求职者,LDA 中主题数目如何确定?
在 LDA 中,主题的数目没有一个固定的最优解。模型训练时,需要事先设置主题数,训练人员需要根据训练出来的结果,手动调参,有优化主题数目,进而优化文本分类结果。
5 后记
LDA 有非常广泛的应用,深层次的懂 LDA 对模型的调优,乃至提出新的模型 以及AI技能的进阶有巨大帮助。只是了解 LDA 能用来干什么,只能忽悠小白。
百度开源了其 LDA 模型,有兴趣的读者可以阅读:https://github.com/baidu/Fami...