语义软分割：《Semantic Soft Segmentation》

《Semantic Soft Segmentation》
   来源：MIT
   主页：http://people.inf.ethz.ch/aksoyy/sss/
   源码：https://github.com/yaksoy/SemanticSoftSegmentation

0 ABSTRACT

   准确地表示图像区域之间的软过渡对于高质量的图像编辑和合成是必不可少的，而当前，这一工作是由技艺纯熟的视觉艺术者来完成，这是一个让人乏味的任务
   本文提出语义软分割（Semantic Soft Segmentation，下面简称SSS）来解决这一问题，使用SSS可以轻松完成复杂的图像编辑任务
   SSS从光谱分割（spectral segmentation）的角度来解决这个问题，提出了一种嵌入图像纹理和颜色特征（texture and color features）以及神经网络产生的高级语义信息（ higher-level semantic information）的图结构（graph structure）；然后通过拉普拉斯矩阵（ Laplacian matrix）全自动特征分解（ eigendecomposition）生成软分割（ soft segments）

1 INTRODUCTION

   选择和组合是图像编辑的核心，比如，局部调整通常从选择开始，组合来自不同图像的元素是生成新内容的一种强大方法；但是，创建一个精确的选择是一项乏味的任务，尤其是在涉及模糊边界和透明度的情况下
   当下，如magnetic lasso 和 magic等这类工具就是为了帮助用户，但它们依赖低端线索，还是严重依赖用户的技艺；此外它们只进行二值选择，需要使用者来细化如毛茸茸的狗狗轮廓这样的软边界。Matting工具可以完成这一边界任务，但还是很单调乏味
   SSS就是来自动解决这一问题的方案，在演示中，可以看出利用SSS可以方便地完成语义分割，图像编辑中的换背景，局部换颜色等等任务

2 RELATED WORK

   1）Soft segmentation
      将图像分解为2个或多个分段，其中每个像素可能属于对个分段

   2）Natural image matting
      对用户定义的前景区域的每像素不透明度（opacity）的估计，matting算法的典型输入是trimap，它定义不透明的前景、透明的背景和不可知的不透明区域
      目前Matting方法也有很多，有兴趣可以看看

   3）Semantic segmentation
      对图像中每个像素进行分类，一个像素只能属于一个类，同一类事物属于同一类，比如一张图像中有多个人，这些人都属于同一类
      关于语义分割的论文就太多了，直接给个github链接，有兴趣可以看看

   4）Instance segmentation
      与语义分割相似，不同的是图像中每个个体是单独实例，比如一张图像中有多个人，这些人属于不同实例
      实例分割，这方面研究也很多，COCO挑战赛有这项，有兴趣可以看看

   5）Panoptic segmentation
      全景分割是近年兴起的，可谓是语义分割和实例分割的结合体，COCO2018挑战赛项目，有兴趣可以看看

3 METHOD

   1）本文寻求自动生成输入图像的软分割，即分解成层（layers），表示场景中存在的对象，包括透明度和软过渡；每个像素都有一个透明值（opacity value）$$\alpha \in [0,1]$$
   $\alpha =0$表示完全透明，$\alpha =1$表示完全不透明，中间值表示不透明程度。如在Matting论文中的模型：

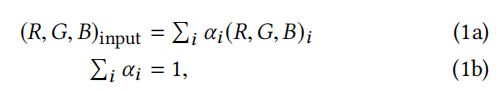
   RGB像素则表示为，每层i的像素值与$\alpha$值的加权和，并且限制在单个像素上和为1

   2）本文采用如《spectral matting》的形式，将制定软分割任务作为特征向量估计问题。这种方法的核心是创建一个拉普拉斯矩阵L，该矩阵表示图像中每对像素属于同一段的可能性。但是spectral matting在建立L矩阵时，采用的是低级的局部颜色分布来构建的，本文提出利用非局部线索和高级语义信息来弥补这块；spectral matting还描述了如何使用稀疏方法从L矩阵中创建特征向量层，本文将改进稀疏方法，已取得更好的结果。图像2展示SSS

3.1 Background

   1）Spectral matting
   首先，引进matting Laplacian，它表现为由局部颜色分布定义的矩阵L；它表达的是局部patch中，像素对之间的关联（affinity），经典的为5x5的像素局部。
   然后，根据用户提供的约束，利用L矩阵，最小化二次型${\mathbf{\alpha }}^{T}L\mathbf{\alpha }$，其中$\mathbf{\alpha }$表示一个向量，是某层的所有$\alpha$组成
   再然后，在随后的工作中，利用特征向量建立了软分割。每段软分割都是L矩阵最小特征值对应的K维特征向量的线性组合
   最后，这些分段是最小化一个能量函数得到的

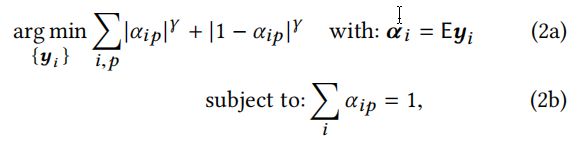
   其中，${\alpha }_{ip}$表示第$i^{th}$分段第$p^{th}$个像素位置的$\alpha$值；E表示有L矩阵的最小特征值对应K维特征向量组成的矩阵；$y_i$表示定义软分割的特征向量对应的线性权值；$\gamma <1$表示稀疏性的控制因子

    spectral matting在图像中包含一个具有不同颜色且识别良好的单一目标时，会产生令人满意的结果，但是在复杂目标或场景下，由于受到仅仅考虑局部低级特征构建L矩阵，识别效果当然较差；本文中将在构建L矩阵时，融入更多语义特征，捕获更高层次的概念，如场景对象，已获得更广阔的图像视野

   2）Affinity and Laplacian matrices
   像素对之间更具有关联，则表示两个像素更相似，0关联的像素是独立的，负关联的像素则可能拥有不同的值。本文中，使用归一化拉普拉斯矩阵来表达这一关联概念

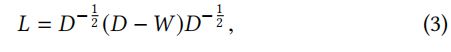
   其中，W表示包含所有像素对之间的关联方阵，D为对应的次数矩阵（degree matrix）

3.2 Nonlocal Color Affinity

   上文中提到了低级关联项，需要改进。一个简单的方法是在matting Laplacian的定义中使用更大的patch，然而，这个选项很快变得不切实际，因为它使拉普拉斯矩阵变得更密集。另一种选择是从非局部邻域采样像素来插入连接，同时在矩阵中保留一些稀疏性，KNN matting和information-flow matting用这种采样做出了良好的结果。然而，这种策略面临着稀疏性和鲁棒性之间的权衡：较少的样本可能会遗漏重要的图像特征，而更多的样本会使计算变得不那么容易处理。

   本文提出了一种基于图像过度分割（oversegmentation）的有指导的采样方法。我们使用SLIC生成2500个压像素，并估计每个压像素与所有半径内的压像素之间的关联，该半径相当于图像大小的20%（nonlocal color affinity）。这种方法的优点是，每一个足够大的特征都被表示为一个压像素，稀疏性仍然很高，因为我们对每个压像素使用一个单一的样本，并且它通过使用一个大半径来链接可能断开的区域，例如，当通过物体上的洞看到背景时候。

   形式上，我们定义，在两个压像素s和t质心之间（距离至少在图像尺寸的20%）的颜色关联$w_{s,t}^C$：

   其中$c_s$和$c_t$为位于[0,1]的s和t压像素的平均颜色；$a_c$和$b_c$为控制关联退化速度和阈值为0的参数；erf为高斯误差函数，取[-1,1]中值，在这里使用它的主要动机是它的sigmoidal shape。

   这种关联本质上确保了颜色非常相似的区域在具有挑战性的场景结构中保持连接，其效果如图3所示

3.3 High-Level Semantic Affinity

   虽然nonlocal color affinity为分割增色不少，尤其在远距离相互作用上，但它毕竟采用还是低级特征，根据作者实验表明，在颜色相近的不同对象分割时，容易出现问题；
   为了解决这一问题，本文增加了语义关联项（semantic affinity term），它激励属于同一场景对象的像素点分为组，抑制不同场景对象分组。即在已有对象识别区域基础上，计算与目标相关的每个像素的特征向量，这个向量是通过神经网络计算出的特征向量（见3.5）。如点p和q属于同一对象，则$||f_p-f_q||\equiv 0$；点r不在同一语义区域内，则$||f_p-f_q||\ll ||f_p-f_r||$
   本文还定义了亚像素（superpixels）级的语义关联，既可增加线性系统的稀疏性，也可减少了过渡区域中不可靠特征向量的负面影响，如图

   亚像素边界不会直接用到线性系统，但在图（ graph）中的链接，是用的亚像素中心；对于每个亚像素s，我们关联它的平均特征向量${\overline{f}}_x$和它的中心$p_s$，则相邻亚像素s和t的语义关联表示为：

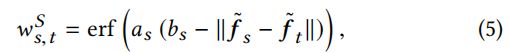
   $a_s$和$b_s$表示控制关联函数的倾斜度（steepness）因子，见3.5；负关联有利于graph断开不同对象，正关联有利益链接同一对象

   与颜色关联（color affinity）不同，语义关联（semantic affinity）只与附近的压像素相关，有利于创建连接的对象。这种非局部颜色关联和局部语义关联的结合，允许创建具有相同语义区域，而空间不连续区域的层（layers）。例如背景中经常出现的绿色植物和天空等元素，使得它们很可能由于遮挡而被分割成几个互不相连的区域。
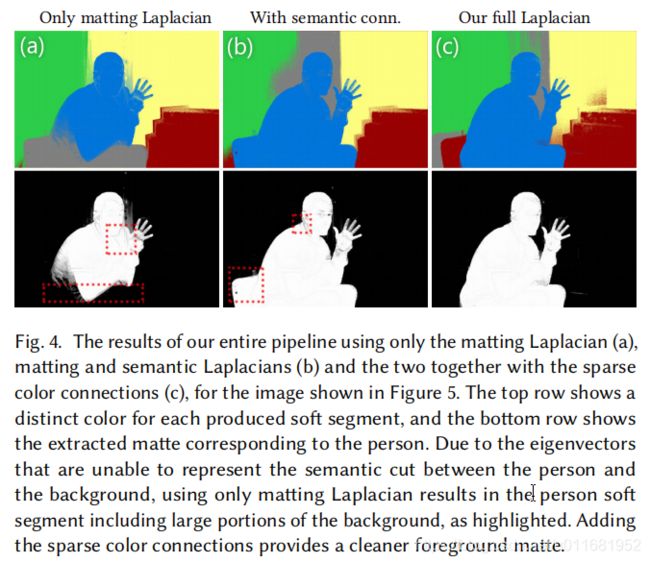
   由于包含了局部语义关联，L的特征向量揭示了对象边界，如图4和图5所示

3.4 Creating the Layers

   使用前面描述的关联来创建层（Layers），从而形成一个拉普拉斯矩阵L。我们从这个矩阵中提取特征向量，并使用两步稀疏化过程从这些特征向量中创建层。

   1）Forming the Laplacian matrix
   根据式3，以及几种关联矩阵的融合，形成拉普拉斯矩阵L：

   $W_l$，$W_s$，$W_c$分别表示Matting关联，局部语义关联，非局部颜色关联；${\sigma }_s$，${\sigma }_c$分别表示对应关联融合权重，都设为0.01

   2）Constrained sparsification
   提取 L 矩阵的 100 个最小特征值对应的特征向量，在式2的优化过程中令 γ = 0.8，与特征向量上使用k-均值聚类来初始化优化不同，我们在特征向量f所表示的像素上使用k-均值聚类。这种初始猜测更符合场景语义，得到了更好的软分割效果。

   我们用这种方法生成了40个层，实际上，其中几个都是0，剩下15到25个非平凡层。通过在这些非平凡层上运行k = 5的k-means算法，我们进一步减少了层数，这些层由它们的平均特征向量表示。这种方法比直接将100个特征向量稀疏化为5层的方法更有效，因为这种大幅度的缩减使得问题过于受限，并且不能产生足够好的结果，尤其是在matting稀疏方面。分组前后初步估计的软段如图7所示

   3）Relaxed sparsification
   为了改善层的稀疏性，选择放宽他们特征向量的线性组合的约束。并不通过调整系数$y_i$来处理，而是通过调节式2中的$\alpha$。
   首先，放宽子空间约束，并且仅确保生成的层保持靠近使用稀疏化约束过程中创建的层$\hat{\alpha }$：

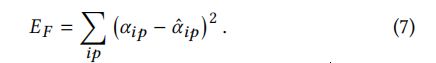
   同时放宽累加为1的要求，作为软约束集成到线性系统中：

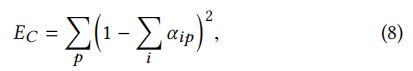
   然后，下面是L定义的能量函数：

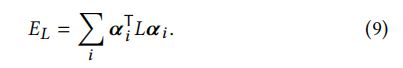
   最后，我们制定了一个适应图像内容的稀疏项（ sparsity term）。直观地，部分像素来自图像中的颜色过渡，因为在许多情况下，它对应于两个场景元素之间的过渡，例如，泰迪熊和背景之间的模糊过渡。 我们使用这种观察来建立一个空间变化的稀疏能量：

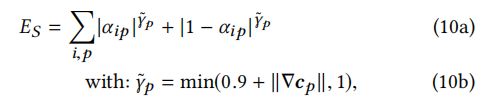
   将这些项放在一起，可以得到：

   我们的空间变化稀疏能量对保持精确的软转换的影响可以从图6中看到：

3.5 Semantic Feature Vectors

   3.3中提到了用特征向量f来定义语义关联项（semantic affinity term），它可以由完成语义分割的神经网络生成。在本文中，将语义分割和度量学习（metric learning）相结合，具体见补充资料

   本文基础特征提取网络采用DeepLab-Resnet-101《 DeepLab: Semantic Image Segmentation with Deep Convolutional Nets》结合度量学习《Deep metric learning using triplet network》，目的是最大化不同对象的L2距离

   我们在训练时，不是使用图像的所有像素，而是为所有像素生成特征，只使用一组随机采样的特征来更新网络。该网络使具有相同ground-truth类的样本特征之间的距离最小化，反之则使距离最大化。由于我们只使用这个线索（cue），即两个像素是否属于同一个类别，所以在训练中不使用特定的对象类别信息。因此，我们的方法是一种与类无关的方法，这符合我们语义软分割的总体目标，因为我们的目标是创建覆盖语义对象的软段，而不是对图像中的对象进行分类。为了利用更多具有计算效率的数据，我们使用了一个稍微修改过的N-pair loss

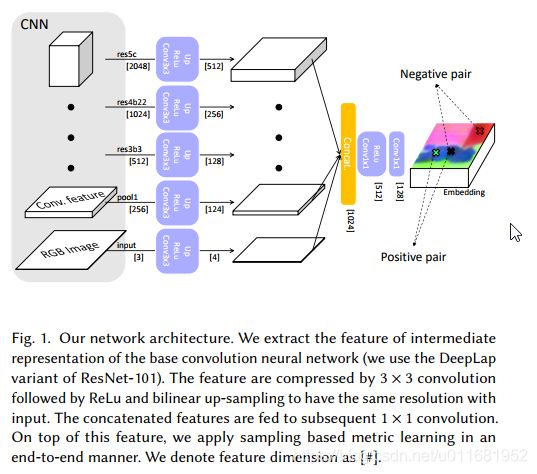
   我们对该网络进行COCO-Stuff数据集的语义分割任务训练。我们使用引导过滤器对该网络生成的特征图进行细化，使其与图像边缘保持良好对齐，然后使用主成分分析(PCA)将维数降为3，图8显示了这些预处理步骤。

   虽然原始的128维向量可以很好地覆盖我们可能遇到的所有内容，但是每个图像只显示了其中的一小部分，因此降低维数可以提高每个维数的精度。最后，我们对向量进行标准化，使其取值于[0,1]。这使得设置参数更容易，特别是在改变特征向量定义的情况下。对于我们给出的所有结果，我们将Eq. 5中的as和bs分别设为20和0.2

3.6 Implementation Details

   我们使用MATLAB中可用的稀疏特征分解和直接求解器对算法的约束稀疏化阶段进行概念验证，这一步大约需要3分钟的640*480图像。松弛稀疏化步骤采用MATLAB的预条件共轭梯度优化实现。每次迭代通常在50到80次迭代中收敛，整个过程大约需要30秒，算法的运行时间随像素的增加而线性增长

4 EXPERIMENTAL ANALYSIS

4.1 Spectral Matting and Semantic Segmentation

   

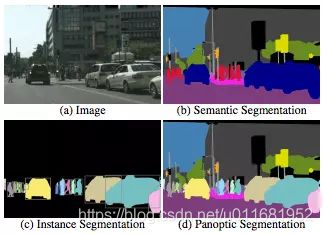
   可以明显看出SSS在分割主体边缘过度区域，优于其他方法，如头发，猫耳朵等

4.2 Natural Image Matting

   

   近年来Matting方法其实取得很大进步，但是呢，它们很依赖trimap的精度

4.3 Soft Color Segmentation

   

4.4 Using Semantic Soft Segments for Image Editing

   

   能准确分割对象，当然换个背景还不是小问题；这相当依赖边界过度区域的精度，若存在损失，融合背景时，会出现白边等

5 LIMITATIONS AND FUTURE WORK

   虽然我们能够生成精确的图像软分段，但在我们的原型实现中，我们的求解器并没有针对速度进行优化。因此，640*480图像的运行时间在3到4分钟之间。我们的方法可以通过多种方法来优化效率，例如多尺度求解器，但是线性求解器和特征分解的有效实现超出了本文的范围

6 RESULT