《OpenCv视觉之眼》Python图像处理十五 :Opencv图像处理之图像缩放、旋转和平移原理及实现

本专栏主要介绍如果通过OpenCv-Python进行图像处理，通过原理理解OpenCv-Python的函数处理原型，在具体情况中，针对不同的图像进行不同等级的、不同方法的处理，以达到对图像进行去噪、锐化等一系列的操作。同时，希望观看本专栏的小伙伴可以理解到OpenCv进行图像处理的强大哦，如有转载，请注明出处(原文链接和作者署名)，感谢各位小伙伴啦！
前文参考：
《OpenCv视觉之眼》Python图像处理一 :Opencv-python的简介及Python环境搭建
《OpenCv视觉之眼》Python图像处理二 :Opencv图像读取、显示、保存基本函数原型及使用
《OpenCv视觉之眼》Python图像处理三 :Opencv图像属性、ROI区域获取及通道处理
《OpenCv视觉之眼》Python图像处理四 :Opencv图像灰度处理的四种方法及原理
《OpenCv视觉之眼》Python图像处理五 :Opencv图像去噪处理之均值滤波、方框滤波、中值滤波和高斯滤波
《OpenCv视觉之眼》Python图像处理六 :Opencv图像傅里叶变换和傅里叶逆变换原理及实现
《OpenCv视觉之眼》Python图像处理七 :Opencv图像处理之高通滤波和低通滤波原理及构造
《OpenCv视觉之眼》Python图像处理八 :Opencv图像处理之图像阈值化处理原理及函数
《OpenCv视觉之眼》Python图像处理九 :Opencv图像形态学处理之图像腐蚀与膨胀原理及方法
《OpenCv视觉之眼》Python图像处理十 :Opencv图像形态学处理之开运算、闭运算和梯度运算原理及方法
《OpenCv视觉之眼》Python图像处理十一 :Opencv图像形态学处理之顶帽运算与黑帽运算
《OpenCv视觉之眼》Python图像处理十二 :Opencv图像轮廓提取之基于一阶导数的Roberts算法、Prewitt算法及Sobel算法
《OpenCv视觉之眼》Python图像处理十三 :Opencv图像轮廓提取之基于二阶导数的Laplacian算法和LOG算法
《OpenCv视觉之眼》Python图像处理十四 :Opencv图像轮廓提取之Scharr算法和Canny算法

上次博客，我们结束了基本图像处理的全部过程，本来本次博客是通过OpenCV进行项目实战的，但自己发现前面忘记讲解了OpenCV实现图像缩放和旋转的原理，于是本次博客作为一个补充讲解，因为图像的旋转和缩放在进行图像增强或者对于图像美化来说是一个重点，掌握原理才能更好的实现对图像的处理，因此在该系列的第15节作为一个补充讲解，一起学习吧！

一、图像缩放

1、图像缩放原理

1）、图像缩放简介
在计算机图像处理和计算机图形学中，图像缩放（image scaling）是指对数字图像的大小进行调整的过程。图像缩放是一种非平凡的过程，需要在处理效率以及结果的平滑度（smoothness）和清晰度（sharpness）上做一个权衡。当一个图像的大小增加之后，组成图像的像素的可见度将会变得更高，从而使得图像表现得“软”。相反地，缩小一个图像将会增强它的平滑度和清晰度。

图像缩放有很多种算法，最简单的方法为邻域插值，即将每一个原像素原封不动地复制映射到扩展后对应四个像素中，这种方法在放大图像的同时保留了所有的原图像的所有信息，但是会产生锯齿现象。
双线性插值的效果对于放大的图像而言较领域插值来得平滑，但是却使得图像变得模糊而且仍然会有一部分锯齿现象。双三次插值更好比双线性插值更好。
2）、图像缩放原理
本次博客，只讲解图像缩放的基本原理，邻域插值，如下：

• 假设我们有一张原始图（源图，source），大小为3*3：
  
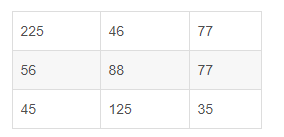
• 想要放大为4*4的目标图（destination）：
  
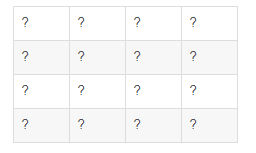
• 那么邻域插值公式原理便如下所示：
  
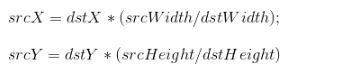
  因此，以上公式便作为我们图像缩放函数构造的基本原理，现在就进行图像缩放函数的构造吧！

2、图像缩放函数构造

1）、图像缩放功能函数构造

'''
    图像处理之图像缩放
'''
#图像缩放函数构造
def zoom(img,factor): #img为需要进行缩放的图像，factor为图像缩小因子(0-1)或者图像尺寸(多少x多少),输入为数组，数组长度为1表示为缩放因子，长度为2表示为缩放尺寸
    #读取图片的高和宽和通道数
    h,w,c=img.shape 
    if len(factor)==1:
        #定义缩放图片的尺寸，0.5位缩放因子，缩放为原来的0.5倍
        h1,w1=int(h*factor[0]),int(w*factor[0])
    elif len(factor)==2:
        h1,w1=factor
    else:
        print("输入错误，请输入数组，长度为1或者为2！")
    #定义空白图像，用于存放缩放后的图片像素
    img1=np.zeros((h1,w1,c),np.uint8) 
    #遍历图像缩放像素
    for i in range(h1): 
        for j in range(w1):
            i1=int(i*(h*1.0/h1))
            j1=int(j*(w*1.0/h1))
            img1[i,j]=img[i1,j1]
    return img1

2）、读取图像，进行图像缩放

import cv2
import numpy as np
#np.set_printoptions(threshold=np.inf)  #打印数组中的全部内容
#读取图像
img=cv2.imread("my.jpg")
#调用图像缩小函数进行图像缩小
zoom=zoom(img,[250,250])#将图像缩放为250x250尺寸的
#图像显示
cv2.imshow("src",img)
cv2.imshow("zoom",zoom)
cv2.waitKey(0)

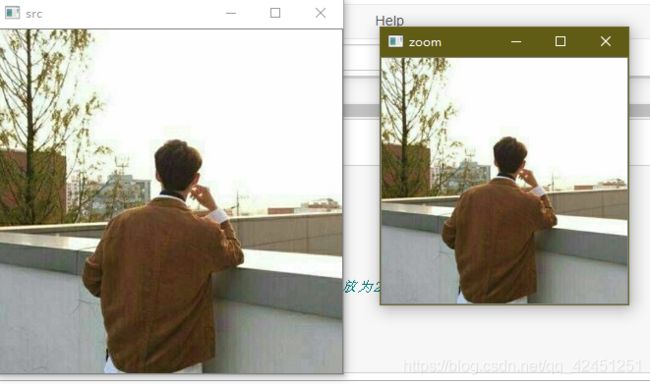
（1）、首先，我们将图像设置为250x250的尺寸进行缩小：zoom=zoom(img,[250,250])

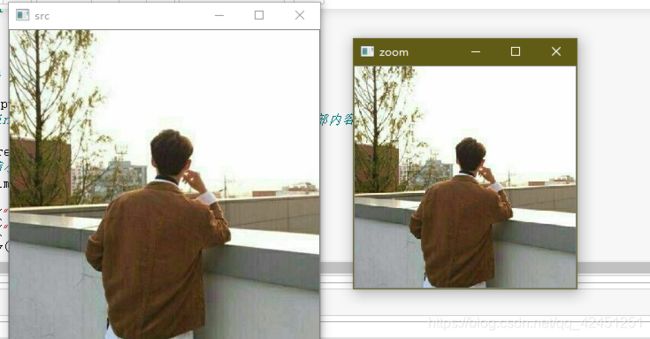
（2）、通过缩放因子进行缩小，缩小为原图的0.5倍大小：zoom=zoom(img,[0.5])

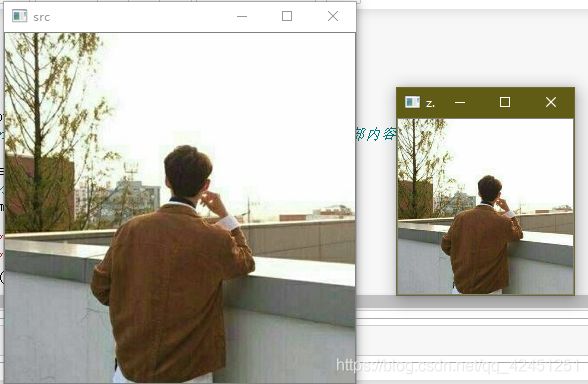
（3）、设置图像尺寸为(400x400)，将图像进行放大：zoom=zoom(img,[400,400])

（4）、设置图像缩放因子为1.2，将图像放大为原图的1.2倍：zoom=zoom(img,[1.2])

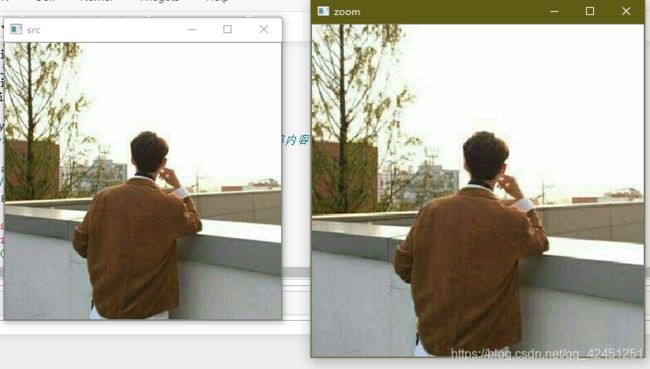
通过以上原理，我们自行构造图像缩放功能函数，在进行图像缩放的同时，应该注意，图像的放大和缩小是不可逆的，不对称的，放大后的图像再进行缩小不是原图哦，图像放大是通过插值像素完成的，和原始像素是有区别的，如果放得太大，图像就会模糊，这样的图像再经过以上的缩小是回不去的，如下：

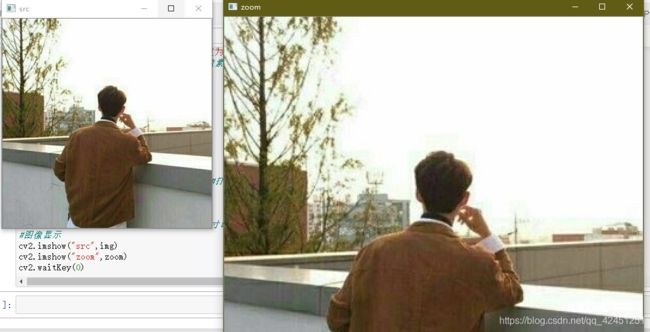
由上面可以看出，图像放大后会过于模糊而导致不清晰！

3、图像缩放OpenCV库函数使用方法

在OpenCV中，图像缩放通过resize()函数实现，如下介绍
1）、缩放函数函数原型：
result = cv2.resize(src, (sizeX,sizeY))
result = cv2.resize(src, fx, fy)

• src：需要缩放的图像
• (sizeX,sizeY)：目标图像的尺寸：通过直接设置尺寸实现
• fx, fy：目标图像的尺寸：通过缩放因子实现，在原图的基础上缩小或者放大

2）、图像缩放库函数使用

'''
    图像处理之图像缩放OpenCV库函数使用
'''
#读取图像
img=cv2.imread("my.jpg")
#调用图像缩小函数进行图像缩小
zoom=cv2.resize(img, (250,250))#将图像缩放为250x250尺寸的
#或者通过缩放因子实现，如下：
#zoom=cv2.resize(img,fx=0.5, fy=0.5)
#图像显示
cv2.imshow("src",img)
cv2.imshow("zoom",zoom)
cv2.waitKey(0)

---

二、图像旋转

图像旋转主要确定旋转中心和旋转角度，然后对图像的像素进行交换就好，具体原理如下

1、图像旋转原理

1）、图像旋转简介
图像旋转是指图像以某一点为中心旋转一定的角度，形成一幅新的图像的过程。当然这个点通常就是图像的中心。既然是按照中心旋转，自然会有这样一个属性：旋转前和旋转后的点离中心的位置不变。
2）、图像旋转原理
设（x0, y0）是旋转后的坐标，（x, y）是旋转前的坐标，(m,n)是旋转中心，a是旋转的角度，(left,top)是旋转后图像的左上角坐标，则公式如下：
$$\left[\begin{array}{ccc}{x}_0& y_0& 1\end{array}\right]=\left[\begin{array}{ccc}x& y& 1\end{array}\right]\left[\begin{array}{ccc}1& 0& 0\\ 0& -1& 0\\ -m& n& 1\end{array}\right]\left[\begin{array}{ccc}\cos (a)& -\sin (a)& 0\\ sin(a)& \cos (a)& 0\\ 0& 0& 1\end{array}\right]\left[\begin{array}{ccc}1& 0& 0\\ 0& -1& 0\\ m& n& 1\end{array}\right]$$
以上原理可以理解为，先将图像平移到旋转点，然后进行旋转，最后将图像平移回去；因此，通过以上公式，我们便可以自行设计出图像旋转函数，进行图像旋转

2、图像旋转函数构造

1）、图像旋转功能函数构造

'''
    图像处理之图像旋转功能函数构造
'''
def rotate(img,a):
    #读取图片的高和宽和通道数
    h,w,c=img.shape 
    #计算对角线长度作为新图像的长和高，因为旋转会有一部分图像在原图像外部
    a1=np.pi*a/180
    r=np.sqrt(h**2+w**2)/2
    #定义空白图像，用于存放旋转后的图片像素
    img1=np.zeros((h,w,c),np.uint8) 
    #确定旋转中心
    x=int(h/2)
    y=int(w/2)
    #遍历图像缩放像素
    for i in range(h): 
        for j in range(w):
            a=np.array([i,j,1])#公式中的第一个矩阵
            b=np.array([[1,0,0],[0,-1,0],[-x,y,1]])#公式中的第二个矩阵
            c=np.array([[np.cos(a1),-np.sin(a1),0],[np.sin(a1),np.cos(a1),0],[0,0,1]])#公式中第三个矩阵
            d=np.array([[1,0,0],[0,-1,0],[x,y,1]])#公式中第四个矩阵
            M=np.dot((np.dot((np.dot(a,b)),c)),d)
            if -1<int(M[0])<h and -1<int(M[1])<w:
                img1[i,j]=img[int(M[0]),int(M[1])]
    return img1  

2）、读取图像，实现图像旋转功能

import cv2
import numpy as np
#np.set_printoptions(threshold=np.inf)  #打印数组中的全部内容
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = ['SimHei'] #显示中文
#读取图像
img=cv2.imread("my.jpg")
#对原图进行格式转换，方便matplotlib图像显示
img=cv2.cvtColor(img,cv2.COLOR_BGR2RGB)
#调用图像旋转函数，进行30、45、60、90度旋转
rotate1=rotate(img,30)
rotate2=rotate(img,45)
rotate3=rotate(img,60)
rotate4=rotate(img,90)
#图像显示
titles = [ '30度旋转', '45度旋转', '60度旋转', '90度旋转']  
images = [rotate1, rotate2, rotate3, rotate4]  
for i in range(4):
    plt.subplot(2,2,i+1), plt.imshow(images[i],)  
    plt.title(titles[i])  
    plt.axis('off')#关闭坐标轴  设置为on则表示开启坐标轴
plt.show()  

注意：以上通过原理编写的函数实现顺时针旋转！

3、图像旋转OpenCV库函数使用方法

OpenCV官方给出的库函数中，图像旋转主要调用getRotationMatrix2D()函数和warpAffine()函数实现，绕图像的中心旋转，如下介绍
1）、getRotationMatrix2D()函数原型：M = cv2.getRotationMatrix2D((cols/2, rows/2), 30, 1)

• (cols/2, rows/2)：旋转中心
• 30：选择角度
• 1：旋转缩放比例，1为原始比例

2）、warpAffine()函数原型：rotated = cv2.warpAffine(src, M, (cols, rows))

• src：需要进行旋转的图像
• M：旋转参数，通过getRotationMatrix2D()函数得出
• (cols, rows)：原始图像宽高

3）、OpenCV图像旋转库函数使用

'''
    图像处理之图像旋转OpenCV库函数使用
'''
import cv2  
import numpy as np  
#读取图片
src = cv2.imread('my.jpg')
#原图的高、宽 以及通道数
rows, cols, channel = src.shape
#绕图像的中心旋转
#参数：旋转中心 旋转度数 scale
M = cv2.getRotationMatrix2D((cols/2, rows/2), 90, 1) #绕中心旋转90度原图
#参数：原始图像 旋转参数 元素图像宽高
rotated = cv2.warpAffine(src, M, (cols, rows))
#显示图像
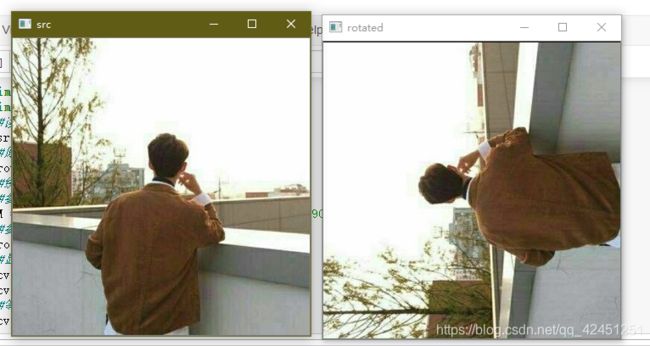
cv2.imshow("src", src)
cv2.imshow("rotated", rotated)
#等待显示
cv2.waitKey(0)

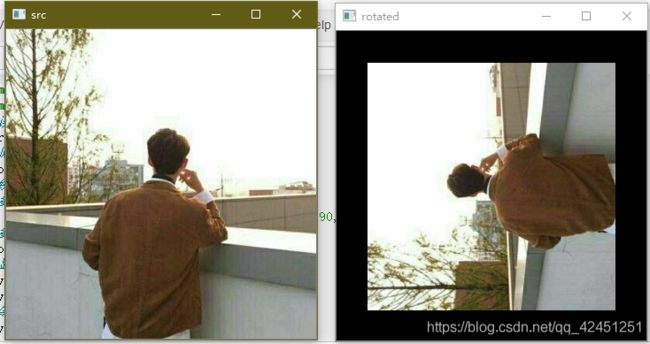
• 缩小为原来的0.8倍再进行90度旋转：M = cv2.getRotationMatrix2D((cols/2, rows/2), 90, 0.8)
  

• 放大为原来的1.2倍再进行90度旋转：M = cv2.getRotationMatrix2D((cols/2, rows/2), 90, 1.2)
  

---

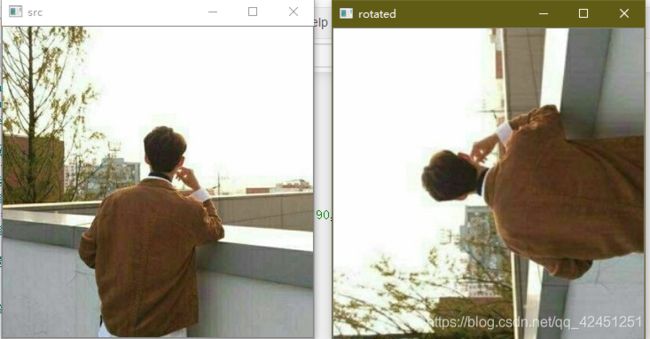
三、图像平移

对于图像平移比较简单，就是单纯的将像素上下左右赋值就好，具体如下介绍

1、图像平移原理

图像平移：设（x0, y0）是缩放后的坐标，（x, y）是缩放前的坐标，dx、dy为偏移量，则公式如下：

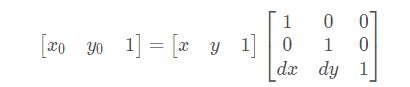
后面包含dx和dy的矩阵为平移矩阵

2、图像平移函数构造

1）、图像平移函数功能构造

'''
    图像处理之图像平移
'''
#图像缩放函数构造
def translation(img,factor): #factor为偏移量，即为平移量输入格式为[20,20],理解为向下向右平移20个像素
    #读取图片的高和宽和通道数
    h,w,c=img.shape 
    #定义空白图像，用于存放平移后的图片像素
    img1=np.zeros((h,w,c),np.uint8) 
    dx,dy=factor
    #遍历图像缩放像素
    for i in range(h-dx): 
        for j in range(w-dy):
            a=np.array([i,j,1])
            b=np.array([[1,0,0],[0,1,0],[abs(dx),abs(dy),1]])
            M=np.dot(a,b)
            #print(M)
            if dx>=0 and dy>=0:
                img1[M[0],M[1]]=img[i,j]  
            if dx<=0 and dy<=0:
                if M[0]<h and M[1]<w:
                    img1[i,j]=img[M[0],M[1]]
    return img1

2）、读取图像，进行图像平移

import cv2
import numpy as np
#np.set_printoptions(threshold=np.inf)  #打印数组中的全部内容
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = ['SimHei'] #显示中文
#读取图像
img=cv2.imread("my.jpg")
#对原图进行格式转换，方便matplotlib图像显示
img=cv2.cvtColor(img,cv2.COLOR_BGR2RGB)
#调用图像平移函数进行图像上下左右平移
translation1=translation(img,[-100,0])
translation2=translation(img,[100,0])
translation3=translation(img,[0,-100])
translation4=translation(img,[0,100])
#图像显示
titles = [ '向上平移', '向下平移', '向左平移', '向右平移']  
images = [translation1, translation2, translation3, translation4]  
for i in range(4):
    plt.subplot(2,2,i+1), plt.imshow(images[i])  
    plt.title(titles[i])  
    plt.axis('off')#关闭坐标轴  设置为on则表示开启坐标轴
plt.show()  

3、图像平移OpenCV库函数使用方法

图像平移首先定义平移矩阵M，再调用warpAffine()函数实现平移，如下技术
1）、图像平移OpenCV库函数原理
M = np.float32([[1, 0, x], [0, 1, y]])
shifted = cv2.warpAffine(image, M, (image.shape[1], image.shape[0]))
2）、图像平移OpenCV库函数使用

'''
    图像处理之图像平移OpenCV库函数使用
'''
import cv2  
import numpy as np
import matplotlib.pyplot as plt
 
#读取图片
img = cv2.imread('my.jpg')
#对原图进行格式转换，方便matplotlib图像显示
image = cv2.cvtColor(img,cv2.COLOR_BGR2RGB)
#图像平移 下、上、右、左平移
M = np.float32([[1, 0, 0], [0, 1, 100]])
img1 = cv2.warpAffine(image, M, (image.shape[1], image.shape[0]))

M = np.float32([[1, 0, 0], [0, 1, -100]])
img2 = cv2.warpAffine(image, M, (image.shape[1], image.shape[0]))

M = np.float32([[1, 0, 100], [0, 1, 0]])
img3 = cv2.warpAffine(image, M, (image.shape[1], image.shape[0]))

M = np.float32([[1, 0, -100], [0, 1, 0]])
img4 = cv2.warpAffine(image, M, (image.shape[1], image.shape[0]))

#显示图形
titles = [ 'Image1', 'Image2', 'Image3', 'Image4']  
images = [img1, img2, img3, img4]  
for i in range(4):  
   plt.subplot(2,2,i+1), plt.imshow(images[i], 'gray')  
   plt.title(titles[i])  
   plt.xticks([]),plt.yticks([])  
plt.show()  

以上就是本次博客的全部内容，遇到问题的小伙伴记得留言评论，学长看到会为大家进行解答的，这个学长不太冷！

同样是一颗心，有的能装下高山，有的能装下大海，有的却只能装下一己之悲欢。有大心量者，方能有大格局，有大格局者，方能成大气候。心有多大，世界就有多大，梦有多远，脚步就有多远。

陈一月的又一天编程岁月^ _ ^