第十章-HMM模型以及相关推导

隐马尔可夫模型(Hidden Markov Model, HMM)是可用于标注问题的统计学习模型，描述由隐藏的马尔科夫链随机生成的观测序列的过程，属于生成模型，是概率模型的一种。本章主要是总结HMM模型的概率计算算法、学习算法以及预测算法。HMM在语音识别、自然语言处理NLP等领域有着广泛的应用。

概率图模型常常是为了描述随机变量之间的关系（是不是独立的），分为有向图和无向图，而HMM主要用有向图。

概率图模型

在有向图中，用圆圈⭕表示随机变量，可以是一维的，也可以是多维的，既可以是离散随机变量，也可以是连续的，⭕叫做结点，图是由结点和边构成的，在有向图中就是有向边，要描述Y受X影响的，就将X和Y连接起来，并用箭头描述从X指向Y的方向。

随机变量之间的关系

一个箭头可以表示两个随机变量之间的关系，引入条件独立的概念，在概率图模型中，假设有三个随机变量X,Y,Z，一般来说，隐变量在图模型中用⭕表示，如果能观察到一个变量取值的时候，用带阴影的圆\bullet表示。在掷硬币的例子中，第1个结果是观察不到的，用空心圆⭕表示，第2个结果是可以观察到的，用带阴影的圆●表示。为什么要强调隐变量和观测变量，圆是空心⭕还是阴影●会影响到随机变量的依赖性。

第一种情况

随机变量都是空心圆，三个随机变量都是观测不到的。即：
$$P(X,Z)\ne P(X)(Z)$$

第二种情况

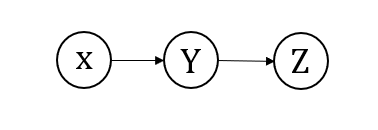
Y是带阴影的圆，随机变量Y是可以观测到的，可得P(X,Z|Y)=P(X|Y)P(Z|Y)，从箭头的指向看，信息是从X传到Y，Y传到Z，一旦将Y固定了，信息的流通相当于被Y观察到的值堵住了，所以当观察到Y时，X和Z就是独立的。

第三种情况

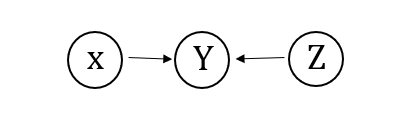
Y指向了两边，这个时候单看X和Z是不独立的，满足P(X,Z) ≠ P(X)P(Z)，如果给定Y，X和Z是独立的，满足
$$P(X,Z|Y)=P(X|Y)P(Z|Y)$$

第四种情况

随机变量满足：
$$P(X,Z)=P(X)P(Z),P(X,Z|Y)\ne P(X|Y)P(Z|Y)$$

HMM模型

定义

隐马尔科夫模型是关于时序的概率模型，描述由一个隐藏的马尔科夫链随机生成不可观测的状态随机序列，再由各个状态生成一个观测而产生观测随机序列的过程。隐藏的马尔科夫链随机生成的状态序列称为状态序列(state sequence),每个状态生成一个观测值，而由此生成的观测的随机序列称为观测序列(observation sequence).

HMM是一个三元组，由初始状态概率向量、状态转移概率矩阵和观测概率矩阵决定，即：
$$\lambda =(A,B,\pi ),其中\pi 是初始状态概率向量，A是状态转移概率矩阵，B是观测概率矩阵$$
定义的形式如下：
$$\begin{gathered} 设Q是所有可能的状态的集合，V是所有可能观测的集合。Q=\{q_1,q_2,q_3...q_N\},V=\{v_1,v_2,..v_M\}, \\ 其中N是所有可能的状态数，M是所有观测数。 \\ I是长度为T的状态序列，O是对应的观测序列。I=(i_1,i_2...i_T),O=(o_1,o_2...o_T). \\ A是状态转移概率矩阵: \\ A=[a_{ij}{]}_{N\times N}，其中a_{ij}=P(i_{t+1}=q_j|i_t=q_t),i=1,2,3...N;j=1,2,...N \\ 是时刻t处于状态q_i的条件下在时刻t+1转移到状态q_j的概率。 \\ B是观测概率矩阵: \\ B=[b_j(k){]}_{N\times M}，其中，b_j(k)=P(o_t=v_k|i_t=q_t),k=1,2,..M;j=1,2,...N \\ 是在时刻t处于状态q_j的条件下生成观测v_k的概率。 \\ \pi 是初始状态概率向量： \\ \pi =({\pi }_i),其中，{\pi }_i=P(i_j=q_i),i=1,2,...N \\ 是在时刻t=1处于状态q_i的概率。 \end{gathered}$$
从定义可知，隐马尔科夫模型做了两个基本假设：

• 齐次马尔可夫性假设。即假设隐藏的马尔可夫链在任意时刻t的状态只依赖于其前一个时刻的状态，与其他时刻的状态以及预测无关，也与时刻t无关。
  $$P(i_t|i_{t-1},o_{t-1},...i_1,o_1)=P(i_t|i_{t-1}),t=1,2,...T$$

• 观测独立性假设。即假设任意时刻的观测只依赖于该时刻的马尔科夫链的状态，与其他时刻观测以及状态无关。
  $$P(o_t|i_T,o_T,o_{T-1},o_{T-1},...,i_{t+1},o_{t+1},i_t,i_{t-1},o_{t-1},...,i_1,o_1)=P(o_t|i_t)$$

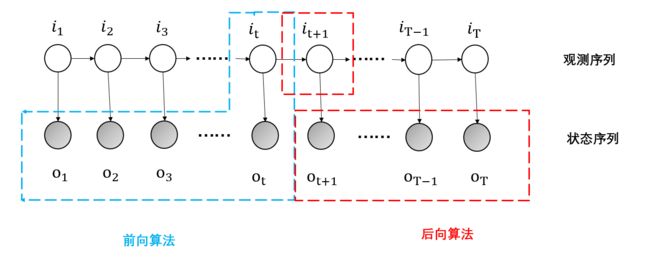
纯粹这样看定义，一堆的数学公式，可能看得不是很懂，那么可以采用概率图的方式来理解HMM模型，如图所示：

[外链图片转存失败(img-AS9wQj1D-1569397355722)(https://img2018.cnblogs.com/blog/842089/201909/842089-20190918152323147-1335165462.png)]

图中的一行⭕表示隐变量的集合，称为状态序列；●表示可观测的集合，称为观测序列，由图可看出，第一个状态变量会影响第二个状态变量，同时还会影响第一个观测变量，依次递推下去，隐马尔可夫模型从状态变量看是一个影响一个的，可以理解成时间序列模型，其适用范围为文本分析，比如标注问题。

三个基本问题

概率计算算法

给定模型和观测序列，那么计算在该模型下观测序列出现的概率的方法有三种：直接计算法、前向算法、后向算法。

直接计算法

$$\begin{gathered} \begin{array}{r}P(O|\lambda )=\sum _{I}P(O|I,\lambda )P(I|\lambda )=\sum _{i_1,i_2,\cdots ,i_T}{\pi }_{i_1}{b}_{i_1}(o_1)a_{i_1{i}_2}{b}_{i_2}(o_2)\cdots a_{i_{T-1}{i}_T}{b}_{i_T}(o_T)\end{array} \\ 首先观察求和符号中b有T项，a有T-1项，\pi 有1项，一共有2T项，求和是从i_1,i_2,\cdots ,i_T不同的取值求和， \\ 对于i_1从状态集合\{q_1,q_2,...q_N\}中取值有N个，i_2取值有N个\dots \dots i_T取值有N个，所以求和范围有N^T项， \\ 要对N^T个范围进行求和，每一个求和范围都需要O(T)个计算量，所以计算复杂度为 \\ 2T\times N^T=2T{N}^T=O(T{N}^T)。 \end{gathered}$$

前向算法

$$\begin{gathered} 输入：隐马尔可夫模型\lambda ，观测序列O。 \\ 输出：观测序列概率P(O|\lambda )。 \\ (1)初值：{\alpha }_1(i)={\pi }_i{b}_i(o_1),i=1,2,\cdots ,N \\ (2)递推，对t=1,2,\cdots ,T-1，{\alpha }_{t+1}(i)=\left[\sum _{j=1}^N{\alpha }_t(j)a_{ji}\right] \\ {b}_i(o_t+1),i=1,2,\cdots ,N \\ (3)终止。P(O|\lambda )=\sum _{i=1}^N{\alpha }_T(i) \end{gathered}$$

可是为何是这样子计算的吗？从数学的角度来推导下具体的算法计算方式——
$$\begin{gathered} 1.首先最终终止的那个公式的推导： \\ 将{\alpha }_t(i)的时刻t的观测值o_1,o_2,\cdots ,o_t及状态值q_i，记作{\alpha }_t(i)=P(o_1,o_2,\cdots ,o_t,i_t=q_i)(忽略\lambda 的条件概率)。 \\ 前向算法用来做的就是概率计算，当\lambda 给定时，观测值o_1,o_2,\cdots ,o_t出现的概率为P(o_1,o_2,\cdots ,o_T)， \\ 这是边缘概率，而P(o_1,o_2,\cdots ,o_T,i_T=q_i)是联合概率，可得 \\ P(o_1,o_2,\cdots ,o_T)=\sum _{i=1}^{N}P(o_1,o_2,\cdots ,o_T,i_T=q_i)=\sum _{i=1}^N{\alpha }_T(i)。 \\ 2.在递推过程中的公式推导: \\ \because 根据定义{\alpha }_{t+1}(i)=P(o_1,o_2,\cdots ,o_t,o_{t+1},i_{t+1}=q_i), \\ 对比{\alpha }_t(i)=P(o_1,\cdots ,o_t,i_t=q_i)少了o_{t+1},i_{t+1}=q_i, \\ \therefore {\alpha }_{t+1}(i)=P(o_1,o_2,\cdots ,o_t,o_{t+1},i_{t+1}=q_i)......................联合概率 \\ =\sum _{j=1}^{N}P(o_1,o_2,...o_t,o_{t+1},i_{t+1}=q_i,i_t=q_j).....................边缘概率 \\ =\sum _{j=1}^{N}P(o_1,o_2,...o_t,i_t=q_j)P(o_{t+1}|i_{t+1}=q_i)P(i_{t+1}=q_i|i_t=q_t) \\ 又\because P(o_{t+1}|i_{t+1}=q_i)=b_i(o_{t+1}) \\ P(i_{t+1}=q_i|i_t=q_j)=a_{ji} \\ P(o_1,o_2,\cdots ,o_t,i_t=q_j)={\alpha }_t(j) \\ \therefore \sum _{j=1}^{N}P(o_1,o_2,\cdots ,o_t,i_t=q_j)P(o_{t+1}|i_{t+1}=q_i)P(i_{t+1}=q_i|i_t=q_j)=\left[\sum _{j=1}^N{\alpha }_t(j)a_{ji}\right]b_i(o_{t+1}) \\ \therefore {\alpha }_{t+1}(i)=\left[\sum _{j=1}^N{\alpha }_t(j)a_{ji}\right]b_i(o_{t+1}) \end{gathered}$$

后向算法

$$\begin{gathered} 输入：隐马尔可夫模型\lambda ，观测序列O。 \\ 输出：观测序列概率P(O|\lambda )。 \\ (1){\beta }_T(i)=1,i=1,2,\cdots ,N。 \\ (2)对t=T-1,T-2,\cdots ,1，{\beta }_t(i)=\sum _{j=1}^N{a}_{ij}{b}_j(o_{t+1}){\beta }_{t+1}(j),i=1,2,\cdots ,N \\ (3)P(O|\lambda )=\sum _{i=1}^N{\pi }_i{b}_i(o_1){\beta }_1(i) \end{gathered}$$

学习问题

已知观测序列，需要估计参数。和之前讲过的很多模型是类似的，需要用一组训练数据集估计模型，之前可能是估计分类超平面，常用的两个方法：监督学习方法、Baum-Welch算法，这两种方法的区别在于哪个算法更贴近应用，这两个方法的学习设定是不一样的。

监督学习方法

$$\begin{gathered} 假设已给训练数据包含S个长度相同的观测序列和对应的状态序列(O_1,I_1),(O_2,I_2),\cdots ,(O_S,I_S)， \\ 那么可以利用极大似然估计法来估计隐马尔可夫模型的参数。具体方法如下： \\ (1)转移概率a_{ij}的估计。 \\ 设样本中时刻t处于状态i时刻t+1转移到状态j记为A_{ij}，那么a_{ij}的估计是： \\ \hat{a}ij=\frac{Aij}{\sum _{j=1}^N{A}_{ij}},i=1,2,\cdots ,N;j=1,2,\cdots ,N \\ (2)观测概率b_j(k)的估计。 \\ 设样本中状态为j观测为k的频数是B_{jk}，那么b_j(k)的估计是： \\ \hat{b}j(k)=\frac{Bjk}{\sum _{k=1}^M{B}_{jk}},j=1,2,\cdots ,N;k=1,2,\cdots ,M \\ (3)初始状态概率{\pi }_i的估计{\hat{\pi }}_i为S个样本中初始状态为q_i的频率。 \end{gathered}$$

$$\begin{gathered} 观测序列和状态序列都有S个样本，需要估计的参数： \\ 首先初始状态\pi ，如果直接用极大似然估计，就是看这S个样本中在初始状态时的各个取值的频率。 \\ 概率转移矩阵A，前一个状态i_t=q_i，后一个状态i_{t+1}=q_j的概率记作a_{ij}，考察在S个观测序列中， \\ 每个观测序列都是有(i_1,i_2,\cdots ,i_{T-1},i_T)，一共有S个这样的马尔可夫链，总计S(T-1)组， \\ 在这些序列组中有多少是观测序列为q_i，然后在这些组中，又有多少组后一项的状态取值为q_j， \\ 这样的比例就是a_{ij}的估计。观测概率b_j(k)的估计也是类似的。 \end{gathered}$$

Baum-Welch算法（EM算法）

KaTeX parse error: Can't use function '$' in math mode at position 101: …0)},\pi_i^{(0)}$̲，得到模型$\lambda^{…

预测问算法

该算法其实就是一个标注问题，已知观测序列和模型参数，让计算机标注每一个观测值的状态，书中提出了两个算法：近似算法（得到的结果并不是全局最优解）、维特比算法（用动态规划思想求最优路径）。但是最常用的还是维特比算法。

维特比算法

维特比算法是求解给定的观测条件下，使得概率最大的状态变量的序列预测，也就是说，求解已知观测序列的出现的概率最大。
$$\begin{gathered} 输入：模型\lambda =(A,B,\pi )和观测O=(o_1,o_2,\cdots ,o_T)。输出：最优路径I^{=}(i_1^{,}{i}_2^{,}\cdots ,i_T^{)}。 \\ (1)初始化。{\delta }_1(i)={\pi }_i{b}_i(o_1),i=1,2,\cdots ,N{\psi }_1(i)=0,i=1,2,\cdots ,N \\ (2)递推，对t=2,3,\cdots ,T{\delta }_t(i)=\underset{1⩽j⩽N}{\max }\left[{\delta }_{t-1}(j)a_{ji}\right]b_i(o_t),i=1,2,\cdots ,N \\ {\psi }_t(i)=\underset{1⩽j⩽N}{\mathrm{argmax}}\left[{\delta }_{t-1}(j)a_{ji}\right],i=1,2,\cdots ,N。 \\ (3)终止。P^{=}\underset{1⩽i⩽N}{\max }{\delta }_T(i)i_T^{=}\underset{1⩽i⩽N}{\max }\left[{\delta }_T(i)\right] \\ (4)最优路径回溯，对t=T-1,T-2,\cdots ,1i_t^{=}{\psi }_{t+1}(i_{t+1}^{)}求得最优路径I^{=}(i_1^{,}{i}_2^{,}\cdots ,i_T^{)}. \end{gathered}$$

具体的例子可以看书中的简单例子。但是要注意的是，在求得每个时刻的观测出现的概率的过程中，一定要记录每个概率最大路径的前一个状态，还有即使在回溯的过程中，要注意通过终点逐步逆向回溯的计算。