机器学习——条件随机场(CRF)原理

机器学习——条件随机场(CRF)原理

1. 条件随机场(CRF)引入

1.1 数学基础

1.1.0 无向概率图

在一个无向图中，任意两个具有边连接的节点x，y，如果从x节点走的y节点是具有一定概率数值的，则这种图被称为无向概率图。马尔科夫随机场就是一种无向的概率图。

1.1.1 团与极大团

在无向图中，任意两个节点之间具有边连接的各个节点集合构成了一个团。在各个团中，如果再加入一个节点，就不能再构成团的节点集合被称为极大团。
例如：在下图中

其中，团为{1,2},{1,3},{2,3},{2,4},{3,4},{3,5},{1,2,3},{2,3,4},{3,5}
极大团为{1,2,3},{2,3,4},{3,5}

1.1.2 势函数

势函数是一个非负的函数，主要用于定义一个概率分布。在马尔科夫随机场的无向图中，多个变量之间的联合概率分布可以基于团分解成多个势函数的乘积，每一个势函数仅仅与一个随机变量相关。

1.1.3 Hammersley-cllifford定理

对于n个变量的马尔科夫随机场，其变量为$X=X_1,X_2,X_3,.......X_n$,在该无向图中，所有的团构成了集合C，团Q∈C，Q对应的X的集合为Q(X)，则联合概率分布为：
$$P(X)=\frac{1}{Z}\ast \prod _{Q\in C}{\phi }_Q(Q(X))$$
其中${\phi }_Q$是函数，Z为规范化因子。

为了进一步的化简运算，只需要计算极大团Q*(X)，就可以简化对对于上面式子的运算。即
$$P(X)=\frac{1}{Z}\ast \prod _{Q^{\ast }\in C^{\ast }}{\phi }_Q(Q^{\ast }(X))$$
其中$C^{\ast }$表示极大团的集合，$Q^{\ast }$表示一个极大团。

1.1.4 分离

设A，B，C分别是无向图马尔科夫随机场的的三个节点集合，如果A中的任意节点想要到B中任意节点（假设可以到达），都需要经过集合C的定点。则称C为A、B的分离集合。我们用图来表示一下：

在上图中，集合A中的节点想要到达集合B中的节点就必须要经过集合C中的节点，所以集合C称为集合A，集合B的分离集。

1.1.5 马尔科夫性

先给出如下实例图：

如图所示的是一个无向图G，其中集合A包括{1,2}两个节点，集合C包括{3,4,5}三个节点，集合B包括{6,7}三个节点。显然，集合C是集合A，B的分离节点。

全局马尔科夫性，集合A,B,C，C是分离集，在给定随机变量$Y_c$的条件下，$Y_a$，$Y_b$条件独立。例如上图所示的在集合C给定的条件下，A,B独立，也就是1,2⊥6,7|3,4,5。
局部马尔科夫性 V是整个无向图G中的任意一点，W是无向图上所有和V相连接的节点集合，O是G上非V和W的节点。则在给定$Y_w$的条件下，$Y_v$和$Y_o$条件独立。在上图中如果V取节点1，W则为{2,3}，则在W给定的条件下，1和4，5,6，7独立。
成对马尔科夫性 U，V是无向概率图G中的任意两个没有边连接的节点。O是除了U，V以外的其他节点，则在$Y_O$给定的条件下，$Y_U$和$Y_V$独立。比如U，V分别取1和7，那么在2,3，4,5，6给定的条件下，1和7条件独立。
满足上面任何的一个特性，该无向概率图就可以成为马尔科夫随机场

1.1.6 特征函数

特征函数是一种实值函数，是用来刻画数据的特征成立的时的函数。例如：

$$f(x,y)=\{\begin{array}{llcccc}1& & if& y=性别& and& x=男或者女\\ 0& & else& & & \end{array}$$
上面是一个简单的特征函数，目的使用来对性别进行判断，当标签Y为性别，输入值X为男或者女的时候函数值为1，否则为0。

2 条件随机场

2.1 条件随机场概述

CRF是一种无向图，判别式的模型。而HMM模型是生成式模型，简单的解释一下，对于HMM模型，我们是利用前一个状态转移的当前的状态，可以理解成是用前一个状态“生成”了当前的状态。而CRF是根据周围节点的状态来“判别”当前状态的概率。

其具体的概念为设X,Y是随机变量，P(Y|X)是在X的条件下Y的概率分布，如果随机变量的Y构成的无向图G(V,E)是一个马尔科夫随机场，则称该无向概率图是条件随机场(CRF)。

这个概念有些抽象，我具体的解释一下，X，Y是两个随机变量，随机变量Y的各个时刻的状态构成了一个无向的概率图G=，其中V表示节点的集合，E表示边的集合，在图G中，每一个节点$Y_v$都满足马尔科夫性，也就是说$P(Y_v|X,Y_Z)=P(Y_v|X,Y_W)$，其中Z表示整个无向图中的所有节点，W表示所有与v相连接的节点。

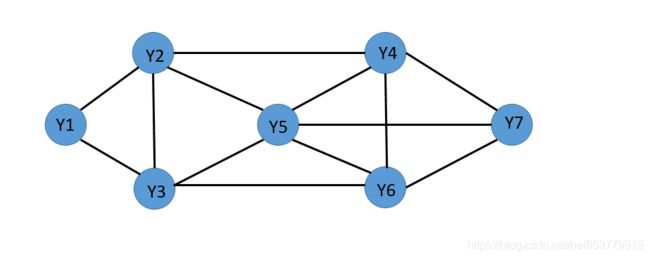
如上图所示，假设随机变量Y的所有取值构成上面的无向图，我们可以看出$P(Y_1|X,Y_Z)=P(Y_1|X,Y_2,Y_3)$，也就是上面的图构成一个条件随机场。

2.2 线性CRF形式

线性的CRF是最为常用的结构，如下图所示：

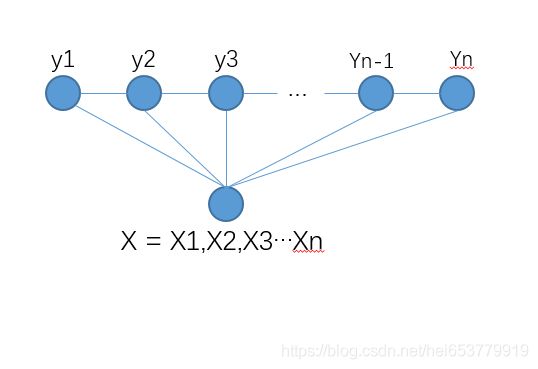
如上所示，在CRF随机场中，如果每一个状态只和前一个状态和后一个状态相关关联，那么我们就可以将无向的概率图结构伸展成线性链条的结构。如上面的$Y_1,Y_2,...Y_n$所示。由于在CRF中，基本形式是$P(Y|X)$，也就是说随机场中的每一个节点都与X相关。所以总的结构如上图所示。

进一步，我们将随机变量X的各种取值展开，就有了下面的结构：

在上面的结构中，我们将随机变量X按照时刻进行展开，也就是说$X_i$都代表着X在第i个时刻的状态值。

举一个例子来说，下面要进行的命名实体识别的过程中，对于一个实体而言，B表示实体的开始的字，E表示实体结束的字。M表示实体的中间的字，S表示单独一个字构成一个实体，O表示其他非实体的字。“EMSO”就代表了随机变量Y的四种取值：“北京市是中国的首都”，这些字对应的就是随机变量X的所有取值，第i个时刻，我们选择一个X的取值$X_i$，与此对应的是一个Y的取值状态，也就是某一个标签值。

$Y_1,Y_2,Y_3,...Y_n$称之为状态序列，$X_1,X_2,X_3...X_n$称之为观察序列。在给定观察序列X的条件下，若随机状态序列Y的条件概率分布P(Y|X)满足随机变量Y满足马尔科夫性，即：
$$P(Y_i|X,Y_1,Y_2,Y_3,....Y_n)=P(Y_i|X,Y_{i-1})$$

也就是说，当前状态$Y_i$仅仅和其相连接的状态$Y_{i-1}$和输入X相关。

2.3 CRF的数学描述

2.3.1 特征函数的定义

我们首先从特征函数的定义开始，根据上面描述的线性CRF的结构特征，我们可以定义出两种特征函数，第一个特征函数是从状态$Y_i$到输出$X_i$的特征序列，也称为节点特征函数，其数学形式为：
$$S_l(Y_i,X,i)=\{\begin{array}{l}1\\ 0\end{array}$$
在这个特征函数中，l∈[1,L]表示的是当前时刻S特征函数的第l个特征函数。i表示时刻，$Y_i$表示当前时刻的状态，X表示当前时刻的输出。当状态$Y_i$输出X符合的期望的时候，特征值为1，否则特征值为0。举个例子来说，当前的观测$X_i$对应的汉字为“北”，如果状态$Y_i$对应的标注为“B”，则特征函数的值为1，如果标记为M，则特征函数值为0。

第二个特征函数是关于状态转移的，也称为是边特征函数，其基本的数学形式为：
$$T_k(Y_{i-1},Y_i,X,i)=\{\begin{array}{l}1\\ 0\end{array}$$
在这个特征函数中，k∈[1,K]表示当前T特征函数的第k个特征函数，i表示时刻，$Y_{i-1},Y_i$分别表示当前时刻的状态和前一个时刻的状态。当前状态符合前一个状态的期望转移的时候特征值为1，否则特征值为0。举个例子来说，对于实体“北京市”，如果前一个时刻的状态为“北”对应的“B”，那么当前时刻如果为“M”，则特征函数值为1，否则为0。

2.3.2 CRF的公式定义

在定义完两种特征函数之后，下面我们给出CRF的基本公式的定义：
$$P(Y|X)=\frac{1}{Z(X)}exp(\sum _{i,k}{\lambda }_k{T}_k(Y_{i-1},Y_i,X,i)+\sum _{i,l}{\mu }_l{S}_l(Y_i,X,i))$$

其中，Z(X)表示归一化因子，Z(X)的基本形式为：
$$Z(X)=\sum _{Y}exp(\sum _{i,k}{\lambda }_k{T}_k(Y_{i-1},Y_i,X,i)+\sum _{i,l}{\mu }_l{S}_l(Y_i,X,i))$$

其中${\lambda }_i和u_i$分别表示的是边特征函数和节点特征函数的权重。

下面，我们来简单的解释一下上面的基本公式，首先是${\sum }_{i,k}{\lambda }_k{T}_k(Y_{i-1},Y_i,X,i)$这一部分主要是对于节点特征函数的求和过程，包含了每一个时刻i，以及每一个节点特征函数$T_k$。这个部分只要刻画的是在每一个时刻，状态的观测值对于状态值的“期望”。符合期望则特征值为1，不符合则特征值为0。

第二个部分，我们要介绍的是${\sum }_{i,l}{\mu }_l{S}_l(Y_i,X,i))$这一部分主要是对于边特征函数求和的过程，包含了每一个时刻i，以及每一个边特征函数$S_l$，其刻画的主要是当前状态标签是否符合前一个时刻状态的“期望”，如果符合，则特征值为1，否则特征值为0。

我们不难发现的是，两个部分的求和的过程是在所有的可能的序列上进行的。

2.3.3 CRF的公式简化

在上面的描述中，我们采用了$S_l$表示节点的特征函数，采用$T_k$表示的边的特征函数，为了表示更加简单，我们将其整理一下：

1. 首先我们假设$M_1$=L,$M_2$=K，也就是说，一共的特征函数包括$M=M_1+M_2$个特征函数。
2. 我们使用一个统一的特征函数进行表示
   $$f_m(Y_{i-1},Y_i,X,i)=T_m(Y_i,Y_{i-1},X,i)，m\in [1,M_1]$$
   $$f_m(Y_{i-1},Y_i,X,i)=S_m(Y_i,Y_{i-1},X,i)，m\in [M_1+1,M]$$
   这样，我们将边的特征函数和节点的特征函数进行整理成一个特征函数。与此同时，我们在对权重进行整理有：
   $$W_m={\lambda }_m，m\in [1,M_1]$$
   $$W_m=s_m，m\in [M_1+1,M]$$

则，整理之后的条件随机场为：
$$P(Y|X)=\frac{1}{Z(X)}exp(\sum _{m=1}^M{W}_m{f}_m(Y,X))$$
向量化表示就是：
$$W=[W_1,W_2,...W_M{]}^T$$
$$F(Y,X)=[f_1(Y,X),f_2(Y,X),......f_M(Y,X){]}^T$$
则有：
$$P_W(Y|X)=\frac{exp(WF(Y,X))}{Z_W(X)}$$

2.3.4 条件随机场的矩阵形式

我们假设Y的取值空间为$[y_1,y_2,....y_q]$，也就是说Y一共有q中取值，我们可以定义一个关于Y的取值的q*q的矩阵Q，其中：
$$Q_i(X)=[Q_i(Y_{i-1},Y_i|X)]$$
$$M_i(Y_{i-1},Y_i|X)=exp(B_i(Y_{i-1},Y_i|X))$$
$$B_i(Y_{i-1},Y_i|X)=$$

3 CRF中的三个问题以及求解过程

3.1 CRF线性链的三个问题

在之前文章机器学习——隐马尔科夫(HMM)原理中，我们提到了HMM模型有三个基本的问题，同样，CRF也存在着三个待求解的问题。值得注意的是，在HMM中，我们将观测序列按照时刻逐个的进行计算，但是在CRF中，我们无需拆开观测序列X，相比而言，CRF更加的容易。下面我们具体描述CRF的三个基本问题：

1. 评估问题： 类似于HMM，CRF也具有概率计算的问题。给定观测序列O和条件随机场，求条件概率$P(Y_t=y_i|O),P(Y_{t-1}=y_{i-1},Yt=y_i|O)$以及相应的数学期望。
2. 学习问题，也就是采用训练数据训练CRF中的权重参数。
3. 解码问题，给定CRF，条件概率分布P(Y|X)，观测序列X，求解条件概率最大的状态序列Y*。

3.2 估计问题求解，

所谓的给定条件随机场，指的就是给定相关的约束条件，即给定相关的特征函数和对应的特征函数的权重值。处理这个问题的基本算法仍然是HMM中的前向后向算法，其中我们定义：
给定的条件随机场：$\gamma$
前向概率：定义${\alpha }_t(i)$，表示在t时刻$Y=y_i$，同时忽略前面状态取值的概率。用公式表达就是：
$${\alpha }_t(i)=P(O_1,O_2,...O_t{Y}_t=y_i|\gamma )$$
后向概率：定义${\beta }_t(i)$，表示表示在t时刻$Y=y_i$，同时忽略后面状态取值的概率。用公式表达就是：
$${\beta }_t(i)=P(O_T,O_{T-1},...,O_t,Y_t=y_i|\gamma )$$
通过前向和后向概率的定义，我们就可以计算出概率为：
$$P(Y_i=y_i|O)=\frac{{\alpha }_t(i{)}^T{\beta }_t(i)}{Z(X)}$$
$$P(Y_{t-1}=y_{i-1},Y_t=y_i|O)=\frac{{\alpha }_t(i{)}^T{B}_i(Y_{t-1},Y_t|O){\beta }_t(i)}{Z(X)}$$
这样，通过类似于前向和后向的推导，我们最终可以确定整个状态序列的概率。

3.3 学习问题

首先，我们再来回顾一下CRF的基本公式：
$$P(Y|X)=\frac{1}{Z(X)}exp(\sum _{i=1}^n{W}_i{F}_i(X,Y))$$
$$Z(X)=\sum _{y}exp(\sum _{i=1}^M{W}_i{F}_i(X,Y))$$
其中有：
$$F(x,y)=\{\begin{array}{l}1，存在着某种关系\\ 0，否则\end{array}$$
在CRF的学习问题中，我们给定了特征函数的定义，也就是说我们实现已经知道了$T_k$和$S_l$的函数定义，我们的目标是获取对应的权重W，为了实现这个目标，我们需要事先定义目标函数，可以采用极大似然估计，这里我们采用的时候极大似然函数作为目标函数：
我们设观测序列和对应的状态序列为$(O^1,Y^1),(O^2,Y^2),...(O^n,Y^n)$，接下来我们设经验概率为$P^{\ast }(O^i,Y^i)$，则对应的极大似然函数为：
$$L(W)=\prod _{x,y}{P}_W(y|x{)}^{P^{-}(x,y)}$$
其中$p^{-}(x,y)$表示的是经验分布，可以从先验知识和训练集样本中得到，进一步，其对数似然函数为：
$$log(L(W))=\sum _{x,y}{P}^{-}(x,y)log(P_W(y|x))$$
为了使用梯度下降算法，我们令$f(w)=-log(L(W))$，则有下面的公式为：
$$\begin{gathered} f(w)=-\sum _{x,y}{P}^{-}(x,y)log(P_W(y|x))=-\sum _{x,y}log{Z}_w(x)-\sum _{x,y}{P}^{-}(x,y)\sum _{m=1}^M{w}_m{f}_m(x,y)= \\ \sum _x{p}^{-}(x)log\sum _{y}exp\sum _{m=1}^M{w}_m{f}_m(x,y)--\sum _{x,y}{P}^{-}(x,y)\sum _{m=1}^M{w}_m{f}_m(x,y) \end{gathered}$$

对W求导之后有：

$$\frac{\partial L(w)}{\partial w}=\sum _{x,y}{P}^{-}(x)P_w(y|x)f(x,y)-\sum _{x,y}{P}^{-}(x,y)f(x,y)$$
在确定了梯度下降算法之后，就可以利用梯度下降算法来迭代求解最优的W了。

3、参考

1.刘建平 条件随机场CRF(三)模型学习与维特比算法解码