pytorch源码解读——RNN/LSTM篇

文章的字母中：

b: batch_size
t: time_step
n: num_feature
h: hidden_size

假设输入数据维度input = (b, t, n)
所设计的LSTM模型如下：

class MYLSTM(nn.Module):

    def __init__(self, input_size, hidden_size, out_size):
        super(MYLSTM, self).__init__()
        self.hidden_size = hidden_size
        self.input_size = input_size
        
        self.lstm = nn.LSTM(
            input_size=self.input_size + self.hidden_size,
            hidden_size=self.hidden_size,
            num_layers=1,
            batch_first=True,
        )

        self.out = nn.Linear(self.hidden_size, out_size)

    def forward(self, x):
        hidden, cell = Variable(torch.zeros(1, x.size(0), self.hidden_size)),\
                       Variable(torch.zeros(1, x.size(0), self.hidden_size))
        for i in range(x.size(1)):
            curx = x[:, i, :].unsqueeze(1)
            curx = torch.cat((curx, hidden.permute(1, 0, 2)), dim=2)
            _, lstm_state = self.lstm(curx, (hidden, cell))
            hidden, cell = lstm_state[0], lstm_state[1]
            outs = self.out(hidden)
        return outs

由于num_layer=1，因此hidden,cell的维度均为(1, b, h)
对于每一个时间步，将其与hidden拼接，得到(b, 1, h + n)维度的curx，此对应下图中红框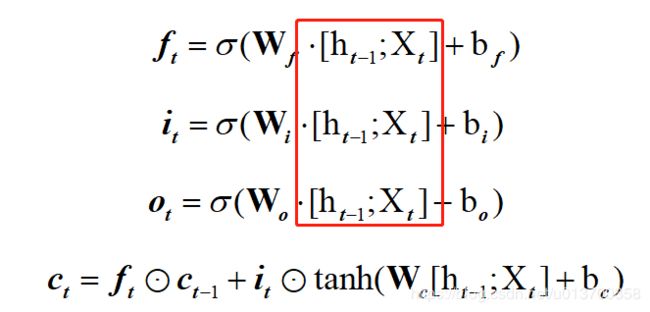
这个整体作为torch中LSTM单元的输入
在modules\rnn.py中，存在这样一段代码：

        if mode == 'LSTM':
            gate_size = 4 * hidden_size
        elif mode == 'GRU':
            gate_size = 3 * hidden_size
        else:
            gate_size = hidden_size
        
		self._all_weights = []
        for layer in range(num_layers):
            for direction in range(num_directions):
                layer_input_size = input_size if layer == 0 else hidden_size * num_directions

                w_ih = Parameter(torch.Tensor(gate_size, layer_input_size))
                w_hh = Parameter(torch.Tensor(gate_size, hidden_size))
                b_ih = Parameter(torch.Tensor(gate_size))
                b_hh = Parameter(torch.Tensor(gate_size))
                layer_params = (w_ih, w_hh, b_ih, b_hh)

                suffix = '_reverse' if direction == 1 else ''
                param_names = ['weight_ih_l{}{}', 'weight_hh_l{}{}']
                if bias:
                    param_names += ['bias_ih_l{}{}', 'bias_hh_l{}{}']
                param_names = [x.format(layer, suffix) for x in param_names]

                for name, param in zip(param_names, layer_params):
                    setattr(self, name, param)
                self._all_weights.append(param_names)

这里的符号跟我上面的图略有不符，因为我习惯于纵向拼接，放下面这个原始的LSTM状态公式可能更好对应一些：

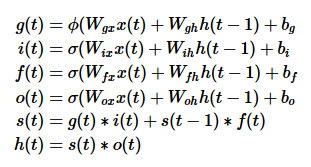
首先根据LSTM网络的特点，或直接看状态计算公式，共有四个地方用到了拼接的输入即计算，因此gate_size = 4 * hidden_size，即相当于把上面的四个Wh和Wx各自合并在一起，各自偏置也合并，方便定义域运算，这个后面还会拆分，分别用于各部分的计算
而由于我们每次的输入均为(b, 1, n + h)，因此layer_input_size = n + h
这样所有需要用到的权重和偏置均已求得，用_all_weights进行包装

此后，同样是在modules\rnn.py文件中

			func = self._backend.RNN(
            self.mode,
            self.input_size,
            self.hidden_size,
            num_layers=self.num_layers,
            batch_first=self.batch_first,
            dropout=self.dropout,
            train=self.training,
            bidirectional=self.bidirectional,
            dropout_state=self.dropout_state,
            variable_length=is_packed,
            flat_weight=flat_weight
        )
        output, hidden = func(input, self.all_weights, hx, batch_sizes)

func将所有参数重新包装并计算，计算过程在_functions\rnn.py中：

    def forward(input, weight, hidden, batch_sizes):
        if batch_first and not variable_length:
            input = input.transpose(0, 1)

        nexth, output = func(input, hidden, weight, batch_sizes)

        if batch_first and not variable_length:
            output = output.transpose(0, 1)

        return output, nexth

上面提到input = (b, 1, n + h)，第一维为batch_size, 即batch_first = True, 于是先将其前两维转置，即此时input = (1, b, n + h)
第一维的1实际代表了LSTM的层数与是否双向，因此此后的运算仅针对单层LSTM进行运算，即此后的input = (b, n + h)
_functions\rnn.py

	hx, cx = hidden
    gates = F.linear(input, w_ih, b_ih) + F.linear(hx, w_hh, b_hh)

    ingate, forgetgate, cellgate, outgate = gates.chunk(4, 1)

    ingate = torch.sigmoid(ingate)
    forgetgate = torch.sigmoid(forgetgate)
    cellgate = torch.tanh(cellgate)
    outgate = torch.sigmoid(outgate)

    cy = (forgetgate * cx) + (ingate * cellgate)
    hy = outgate * torch.tanh(cy)

    return hy, cy

input = (b, n + h), w_hh = (4 * h, h), w_ih = (4* h, n + h)
F.linear是线性操作，无论是CNN、RNN都很常用，其定义如下：

def linear(input, weight, bias=None):
    r"""
    Applies a linear transformation to the incoming data: :math:`y = xA^T + b`.

    Shape:

        - Input: :math:`(N, *, in\_features)` where `*` means any number of
          additional dimensions
        - Weight: :math:`(out\_features, in\_features)`
        - Bias: :math:`(out\_features)`
        - Output: :math:`(N, *, out\_features)`
    """
    if input.dim() == 2 and bias is not None:
        # fused op is marginally faster
        return torch.addmm(bias, input, weight.t())

    output = input.matmul(weight.t())
    if bias is not None:
        output += bias
    return output

比较容易看懂，返回input * weight.t() + bias这样的矩阵
于是经过线性变换后，返回的gates = (b, 4 * h)
然后通过chunk()函数，将gates的第一维切分为四份
于是ingate, forgetgate, cellgate, outgate = (b, h)
分别对ingate forgetgate outgate作sigmoid，对cellgate作tanh，注意 * 运算是点积，而不是矩阵乘法，前述代码配合下图饮用更佳，感觉均能一一对应：

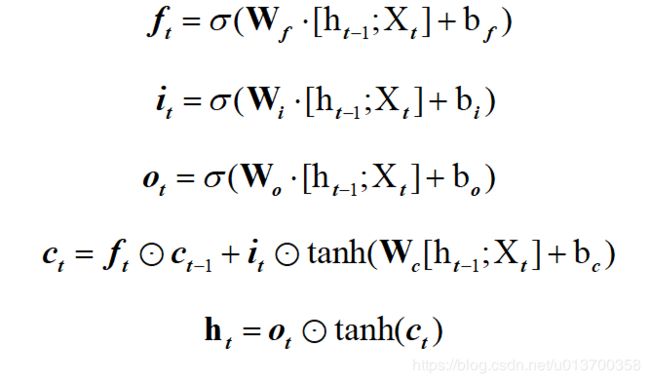
如此即结束了第一个时间步的hidden、cell计算，有多少个时间步，循环迭代即可，最后一步的hidden即可作为最终输出