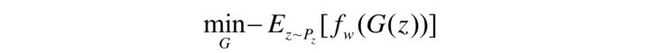Pytorch之GAN实战

AE,VAE原理

• 原理（encoder-neck-reconstruct,降维）

  • 自动编码机Auto-Encoder (AE)由两部分encoder和decoder组成，encoder输入x数据，输出潜在变量z，decoder输入z然后输出一个x’，目的是让x’与x的分布尽量一致，当两者完全一样时，中间的潜在变量z可以看作是x的一种压缩状态，包含了x的全部feature特征，此时监督信号就是原数据x本身。

• 损失函数

• 两个变种：

• 加噪声：防止只学到表层特征，对输入图片添加噪声

• dropout：不依赖于所有上层神经元，增加模型鲁棒性

• 对抗 AE：

  想让经过encoder后的数据符合某一分布，防止对于任意的分布都会重建为相同的值，我们可以增加一个discriminator鉴别。

• VAE：变分自编码器

  • 变分自动编码机VAE是自动编码机的一种扩展，它假设输出的潜在变量z服从一种先验分布，如高斯分布。这样，在训练完模型后，我们可以通过采样这种先验分布得到z’，这个z’可能是训练过程中没有出现过的，但是我们依然能在解码器中通过这个z’获得x’，从而得到一些符合原数据x分布的新样本，具有“生成“新样本的能力。
  • 我们通过两个独立的损失项来优化网络，这两个损失项分别是生成损失和KL散度。其中，生成损失指的是生成图片和目标图片之间的像素值均方差，它描述的是网络重建图片的精度。KL散度描述的则是隐变量和标准正态分布之间的匹配程度。这里有一个trick，让编码网络生成均值向量和标准差向量，而不是直接生成隐变量。

AutoEncoder实战

class AE(nn.Module):
    def __init__(self):
        super(AE, self).__init__()
        # [b, 784] => [b, 20]
        self.encoder = nn.Sequential(
            nn.Linear(784, 256),
            nn.ReLU(),
            nn.Linear(256, 64),
            nn.ReLU(),
            nn.Linear(64, 20),
            nn.ReLU()
        )
        # [b, 20] => [b, 784]
        self.decoder = nn.Sequential(
            nn.Linear(20, 64),
            nn.ReLU(),
            nn.Linear(64, 256),
            nn.ReLU(),
            nn.Linear(256, 784),
            nn.Sigmoid()
        )
    def forward(self, x): 		#param x: [b, 1, 28, 28]
        batchsz = x.size(0)
        # flatten
        x = x.view(batchsz, 784)
        # encoder
        x = self.encoder(x)
        # decoder
        x = self.decoder(x)
        # reshape
        x = x.view(batchsz, 1, 28, 28)
        return x

VAE实战

class VAE(nn.Module):
    def __init__(self):
        super(VAE, self).__init__()
        # [b, 784] => [b, 20]
        # u: [b, 10] 均值
        # sigma: [b, 10] 方差 (采样正态分布) 
        self.encoder = nn.Sequential(
            nn.Linear(784, 256),
            nn.ReLU(),
            nn.Linear(256, 64),
            nn.ReLU(),
            nn.Linear(64, 20),
            nn.ReLU()
        )
        # [b, 20] => [b, 784]
        self.decoder = nn.Sequential(
            nn.Linear(10, 64),
            nn.ReLU(),
            nn.Linear(64, 256),
            nn.ReLU(),
            nn.Linear(256, 784),
            nn.Sigmoid()
        )
        self.criteon = nn.MSELoss()
    def forward(self, x):	#param x: [b, 1, 28, 28]
        batchsz = x.size(0)
        # flatten
        x = x.view(batchsz, 784)
        # encoder
        # [b, 20], including mean and sigma
        h_ = self.encoder(x)
        # [b, 20] => [b, 10] and [b, 10] 在1维拆分
        mu, sigma = h_.chunk(2, dim=1)
        # reparametrize trick, epison~N(0, 1)
        h = mu + sigma * torch.randn_like(sigma)
        # decoder
        x_hat = self.decoder(h)
        # reshape
        x_hat = x_hat.view(batchsz, 1, 28, 28)
        # kl散度
        kl = 0.5 * torch.sum(
            torch.pow(mu, 2) +
            torch.pow(sigma, 2) -
            torch.log(1e-8 + torch.pow(sigma, 2)) - 1
        ) / (batchsz*28*28)
        return x_hat, kl

GAN原理

GAN受博弈论中的零和博弈启发，将数据(以图片为例)的生成问题视作判别器和生成器这两个网络的对抗和博弈。生成器从给定噪声中（一般是指均匀分布或者正态分布）产生生成的图片，而判别器分辨生成器输出的生成样本与真实样本。前者G网络试图产生更接近真实样本的样本，相应地，后者D网络试图更完美地分辨真实数据与生成数据。这样，两个网络在对抗中进步，在进步后继续对抗，由G网络生成的样本也就越来越完美，越来越逼近真实的样本，达到生成模型的功能。

为了量化以及数学推导，我们设真实数据为x，随机噪声为z，生成网络为G，判别网络为D，那么GAN网络的loss(交叉熵)可以表示为：

其中Pr(x)代表真实样本分布，Pz(z)代表生成样本的分布。D(x)的输出是0-1范围内的一个实数，用来判断这个图片是一个真实图片的概率是多大。通过这样一个极大极小(Max-min)博弈，循环交替地分别优化G和D来训练所需要的生成式网络与判别式网络，直到到达纳什均衡点。所谓循环交替优化，也就是固定G，优化D，一段时间后，固定D再优化G，不断重复上述过程，直到损失函数收敛。

如下图所示，假设在训练开始时，真实样本分布、生成样本分布以及判别模型分别是图中的黑线、绿线和蓝线。可以看出，在训练开始时，判别模型是无法很好地区分真实样本和生成样本的。接下来当我们固定生成模型，而优化判别模型时，优化结果如第二幅图所示，可以看出，这个时候判别模型已经可以较好的区分生成数据和真实数据了。第三步是固定判别模型，改进生成模型，试图让判别模型无法区分生成图片与真实图片，在这个过程中，可以看出由模型生成的图片分布与真实图片分布更加接近，这样的迭代不断进行，直到最终收敛，生成分布和真实分布重合。

DCGAN

2014年提出的最原始的GAN模型在D网络和G网络的网络结构上是通过以多层全连接网络为主体的多层感知机(MLP) 实现的，然而其调参难度较大，训练失败相当常见，生成图片质量也相当不佳(尤其对于复杂的数据集)。

由于卷积神经网络比MLP有更强的拟合与表达能力，并在判别式模型中取得了很大的成果。因此，研究者将CNN引入生成器和判别器，称作深度卷积对抗神经网络(Deep Convolutional GAN)，如下图所示。本质上，DCGAN是在GAN的基础上提出了一种训练架构，并对其做了训练指导，比如用卷积层取代了大部分全连接层，去掉池化层，采用Batch Normalization技术，将判别模型的发展成果引入到了生成模型中。模型结构如下。

DCGAN使用的上采样的操作叫做转置卷积，我们可以通过上采样生成指定大小的图片。

WGAN

DCGAN和朴素GAN在训练时存在一个共同的问题就是可能会产生梯度消失。原因是朴素GAN的目标函数本质上可以等价于优化真实分布与生成分布的JS散度，而JS散度有一个问题就是如果两个分布P,Q离得很远，完全没有重叠的时候，那么JS散度值是一个常数，也就意味此时这一点的梯度为0，产生了梯度消失的情况。而且，当真实分布与生成分布是高维空间上的低维流形时，两者重叠部分的测度为0的概率为1，这也就是朴素GAN调参困难且训练容易失败的原因之一。

针对这种现象，研究者使用Wasserstein-1距离(也叫EM距离)来代替JS散度

其中，$p_r$,$p_g$分别为真实分布和生成分布， $\gamma$为$p_r,p_g$的联合分布，相较于JS散度，Wasserstein-1距离的优点是即使$p_r,p_g$两个分布不重叠，Wasserstein-1距离依旧可以清楚地反应出两个分布的距离。为了与GAN相结合，将其转换成对偶形式

上式中，$f_w(x)$表示判别器，WGAN不再需要将判别器当作0-1分类将其值限定在[0,1]之间。而是fw越大，表示其越接近真实分布，反之，就越接近生成分布。此外， $f_w(x)$ 满足1-Lipschitz约束。由于Lipschitz连续在判别器上是难以约束的，因此，采用权重剪枝代替1-Lipschitz约束，即要求参数w ∈ [−c, c]，这样判别器的目标函数为：

生成器的损失函数为：

WGAN的贡献在于，从理论上阐述了因生成器梯度消失而导致训练不稳定的原因，并用1-Wasserstein距离替代了Jensen-Shannon散度，在理论上解决了梯度消失问题。

WGAN-GP

WGAN虽然在理论上解决了梯度消失问题，但是也有很多缺点。其使用权重剪枝(clip)来近似替代1-Lipschitz约束，但是其实这两个条件并不等价，而且满足1-Lipschitz约束的情况多数不满足权重剪枝约束，因此还是产生了很多效果不好的情况。这时，有研究者提出了带梯度惩罚的WGAN(WGAN with gradient penalty)，也就是WGAN-GP模型。将1-Lipschitz约束正则化，通过把约束写成目标函数的惩罚项，来近似1-Lipschitz约束条件。效果还是很好的。

因而，WGAN-GP的目标函数为

WGAN-GP的贡献在于，它用正则化的形式表达了对判别器的约束，基本从理论和实验上解决了梯度消失的问题，并且具有强大的稳定性，几乎不需要调参，在大多数网络框架下训练成功率极高。

GAN实战

class Generator(nn.Module):
    def __init__(self):
        super(Generator, self).__init__()
        self.net = nn.Sequential(
            nn.Linear(2, h_dim),
            nn.ReLU(True),
            nn.Linear(h_dim, h_dim),
            nn.ReLU(True),
            nn.Linear(h_dim, h_dim),
            nn.ReLU(True),
            nn.Linear(h_dim, 2),
        )
    def forward(self, z):
        output = self.net(z)
        return output
class Discriminator(nn.Module):
    def __init__(self):
        super(Discriminator, self).__init__()
        self.net = nn.Sequential(
            nn.Linear(2, h_dim),
            nn.ReLU(True),
            nn.Linear(h_dim, h_dim),
            nn.ReLU(True),
            nn.Linear(h_dim, h_dim),
            nn.ReLU(True),
            nn.Linear(h_dim, 1),
            nn.Sigmoid()
        )
    def forward(self, x):
        output = self.net(x)
        return output.view(-1)
def data_generator():
	# 8中心高斯混合模型生成数据
    scale = 2.
    centers = [
        (1, 0),
        (-1, 0),
        (0, 1),
        (0, -1),
        (1. / np.sqrt(2), 1. / np.sqrt(2)),
        (1. / np.sqrt(2), -1. / np.sqrt(2)),
        (-1. / np.sqrt(2), 1. / np.sqrt(2)),
        (-1. / np.sqrt(2), -1. / np.sqrt(2))
    ]
    centers = [(scale * x, scale * y) for x, y in centers]
    while True:
        dataset = []
        for i in range(batchsz):
            point = np.random.randn(2) * .02
            center = random.choice(centers)
            point[0] += center[0]
            point[1] += center[1]
            dataset.append(point)
        dataset = np.array(dataset, dtype='float32')
        dataset /= 1.414
        yield dataset
def main():
    G = Generator()
    D = Discriminator()
    optim_G = optim.Adam(G.parameters(), lr=1e-3, betas=(0.5, 0.9))
    optim_D = optim.Adam(D.parameters(), lr=1e-3, betas=(0.5, 0.9))
    data_iter = data_generator()
    for epoch in range(50000):
        # 1. train discriminator (5次)
        for _ in range(5):
            x = next(data_iter)
            xr = torch.from_numpy(x)
            predr = D(xr)
            # max predr, 因为要让真实数据输出尽可能大(real)
            lossr = - (predr.mean())

            z = torch.randn(batchsz, 2)
            xf = G(z).detach()	# 训练D网络，G网络上不传梯度
            predf = D(xf)
            # min predf, 因为要让生成数据输出尽可能小(fake)
            lossf = predf.mean()
            
            loss_D = lossr + lossf
            optim_D.zero_grad()
            loss_D.backward()
            optim_D.step()
        # 2. train Generator
        z = torch.randn(batchsz, 2)
        xf = G(z)
        predf = D(xf)
        # max predf, 作为生成器，想让自己生成的fake数据输出尽可能大
        loss_G = - (predf.mean())
        optim_G.zero_grad()
        loss_G.backward()
        optim_G.step()

WGAN-GP

# 模型及数据生成部分相似
def gradient_penalty(D, xr, xf):
    LAMBDA = 0.3
    # only constrait for Discriminator
    xf = xf.detach()
    xr = xr.detach()
    # [b, 1], 随机sample一个均值分布
    t = torch.rand(batchsz, 1)
    t = alpha.expand_as(xr) # 将alpha扩展为xr的维度 -> [b, 2]
    # real 和 fake线性插值，需要求导
    interpolates = t * xr + (1 - t) * xf
    interpolates.requires_grad_()
    
    disc_ip = D(interpolates)
    gradients = autograd.grad(outputs=disc_ip, inputs=interpolates,
                              grad_outputs=torch.ones_like(disc_ip),
                              create_graph=True, retain_graph=True, only_inputs=True)[0]
    gp = ((gradients.norm(2, dim=1) - 1) ** 2).mean() * LAMBDA
    return gp
def main():
    G = Generator()
    D = Discriminator()
    optim_G = optim.Adam(G.parameters(), lr=1e-3, betas=(0.5, 0.9))
    optim_D = optim.Adam(D.parameters(), lr=1e-3, betas=(0.5, 0.9))
    data_iter = data_generator()
    for epoch in range(50000):
        # 1. train discriminator (5次)
        for _ in range(5):
            x = next(data_iter)
            xr = torch.from_numpy(x)
            predr = D(xr)
            # max predr, 因为要让真实数据输出尽可能大(real)
            lossr = - (predr.mean())

            z = torch.randn(batchsz, 2)
            xf = G(z).detach()	# 训练D网络，G网络上不传梯度
            predf = D(xf)
            # min predf, 因为要让生成数据输出尽可能小(fake)
            lossf = predf.mean()
            
            # gradient penalty
            gp = gradient_penalty(D, xr, xf)
            
            loss_D = lossr + lossf + gp
            optim_D.zero_grad()
            loss_D.backward()
            optim_D.step()
        # 2. train Generator
        z = torch.randn(batchsz, 2)
        xf = G(z)
        predf = D(xf)
        # max predf, 作为生成器，想让自己生成的fake数据输出尽可能大
        loss_G = - (predf.mean())
        optim_G.zero_grad()
        loss_G.backward()
        optim_G.step()
)
            loss_D.backward()
            optim_D.step()
        # 2. train Generator
        z = torch.randn(batchsz, 2)
        xf = G(z)
        predf = D(xf)
        # max predf, 作为生成器，想让自己生成的fake数据输出尽可能大
        loss_G = - (predf.mean())
        optim_G.zero_grad()
        loss_G.backward()
        optim_G.step()