深入理解概率图模型(一):有向图模型
文章目录
- 1.Introduction
- 1.1 Chain rule
- 1.2 Conditional independence
- 1.3 Graphical Models
- 1.4 Directed graphical models(Bayes Net)
- 2. An example of DGM: Naive Bayes
- 2.1 Naive Bayes
- 2.2 Naive Bayes in DGM
- 3. Inference
- 3.1 What can we do with such a joint distribution?
- 3.2 Probabilistic Inference
- 4. Learning
- 4.1 The difference between inference and learning
- 4.2 The relationship between inference and learning
- 4.3 Plate notation
- 4.4 Learning from complete data
- 4.5 Learning with missing and/or latent variables
- 5. Conditional independence properties of DGMs(three properties)
- 5.1 D-separation(Global Markov Properties)
- 5.2 Directed Local Markov Property
- 5.3 Ordered Markov Property
- 5.4 The relationships among these properties
- 5.5 Markov blanket in DGM
- 6. Decision
- 参考文献
1.Introduction
1.1 Chain rule
- 通过概率中的链式法则,我们可以很好的表示一个联合概率分布(joint distribution),并且可以使用不同的变量顺序。
( 公式说明:V表示变量的个数,1:V表示集合{1,2,…,V}。为简明起见,我们去掉了对固定参数θ的条件)
p ( x 1 : V ) = p ( x 1 ) p ( x 2 ∣ x 1 ) p ( x 3 ∣ x 2 , x 1 ) . . . p ( x V ∣ x 1 : V − 1 ) p({x_{1:V}}) = p({x_1})p({x_2}|{x_1})p({x_3}|{x_2},{x_1})...p({x_V}|{x_{1:V - 1}}) p(x1:V)=p(x1)p(x2∣x1)p(x3∣x2,x1)...p(xV∣x1:V−1) - 链式法则存在什么问题呢?当变量变得很多,并且变量的维度很高时,计算这些条件概率或者联合概率会变得非常复杂(假设x1,x2为两个离散变量,都有K个状态,则P(x1|x2)就会有K**2个状态)
- 一种解决方案就是:用更简约的条件概率分布(Conditional Probability Distributions),当然这并不使用所有场合,更通俗的来说,它不实用,所以我们需要另一种方法。
1.2 Conditional independence
-
有效地表示大型联合分布的关键是对条件独立性(CI)做出一些假设。
-
我们说 X⊥Y| Z当且仅当条件联合可以写成条件边缘的乘积,即
X ⊥ Y ∣ Z ⇔ p ( X , Y ∣ Z ) = p ( X ∣ Z ) p ( Y ∣ Z ) X \bot Y|Z \Leftrightarrow p(X,Y|Z) = p(X|Z)p(Y|Z) X⊥Y∣Z⇔p(X,Y∣Z)=p(X∣Z)p(Y∣Z) -
让我们看看条件独立为什么如此有用?
假设现在的状态是已观测的,未来是独立于过去的,即下面的公式。这被称作一阶马尔科夫假设(First-order Markov Assumption)
x t + 1 ⊥ x 1 : t − 1 ∣ x t {x_{t + 1}} \bot {x_{1:t - 1}}|{x_t} xt+1⊥x1:t−1∣xt -
当我们运用这一假设到链式法则中时,我们就可以将联合概率写成如下形式:
p ( x 1 : V ) = p ( x 1 ) ∏ t = 1 V p ( x t ∣ x t − 1 ) p({x_{1:V}}) = p({x_1})\prod\limits_{t = 1}^V {p({x_t}|{x_{t - 1}})} p(x1:V)=p(x1)t=1∏Vp(xt∣xt−1)
- 可以看到通过这种假设,我们就大大化简了联合概率的形式。上面的这种模型我们成为一阶马尔科夫链(First-order Markov Chain)
1.3 Graphical Models
- Why Graphical Models?
虽然一阶马尔可夫假设对于定义一维序列上的分布是非常有用的,但是我们如何定义二维图像或3D视频上的分布,或者一般而言,任意变量集合上的分布,这时候图模型就自然而然就来了,它来了! - How we define GM(Graphical Model)?
通过条件独立假设(CI)来表示联合概率的一种方法,其中节点表示随机变量,边表示条件概率(在有向图中,可以理解为因果的关系) - 这篇文章只考虑有向图模型(Directed Graphical Models,DGM)
1.4 Directed graphical models(Bayes Net)
- 一些说法
贝叶斯网络 = 有向图模型 = 信念网络(Belief Networks) = 因果网络(Causal Networks) - 有序马尔科夫性质(Ordered Markov Property)
我们定义马尔科夫性质为这样的假设:一个节点仅依赖于它的直接父类,并不依赖于所有先辈(Predecessors),即
x s ⊥ x p r e d ( s ) \ p a ( s ) ∣ x p a ( s ) {x_s} \bot {x_{pred(s)\backslash pa(s)}}|{x_{pa(s)}} xs⊥xpred(s)\pa(s)∣xpa(s)
其中,pa(s)是s的父节点,pred(s)是s的所有先辈。这是一阶马尔科夫链的推广。
- 通过马尔科夫性质,我们以可重新写出联合概率分布,即:
p ( x 1 : V ∣ G ) = ∏ t = 1 V p ( x t ∣ x p a ( t ) ) p({x_{1:V}}|G) = \prod\limits_{t = 1}^V {p({x_t}|{x_{pa(t)}})} p(x1:V∣G)=t=1∏Vp(xt∣xpa(t))
通过这种条件独立假设,我们大大简化了计算量,减少了很多参数(对比原来的联合概率分布 就知道,这里不做证明)
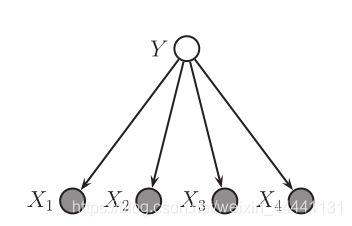
2. An example of DGM: Naive Bayes
2.1 Naive Bayes
- 朴素贝叶斯用来做多分类任务
- 朴素贝叶斯假设当给定观测标签Y时,特征之间是相互独立的,这在现实中很难做到,因为假设太强了,所以称之为“幼稚的”。
- 朴素贝叶斯是生成没模型,我们可以根据假设写下联合概率分布,即:
p ( y , x ) = p ( y ) ∏ j = 1 D p ( x j ∣ y ) p(y,x) = p(y)\prod\limits_{j = 1}^D {p({x_j}|y)} p(y,x)=p(y)j=1∏Dp(xj∣y)
2.2 Naive Bayes in DGM
3. Inference
3.1 What can we do with such a joint distribution?
- 我们已经看到,图形模型提供了一种定义更加紧凑的联合概率方式,那我们可以用这个联合概率来做什么,这个是我们要关注的。
3.2 Probabilistic Inference
- 最主要的作用就是要做概率推断
- 一般的,我们说推理问题是这样的:假设我们有一些随机变量即他们的联合概率分布,并且有参数(在推断过程中,我们一般假设参数θ是已知的)。我们把随机变量组成的向量分割为可观测变量Xv(visible variables)和隐变量Xh(hidden variables),则推断指的就是计算隐变量的后验概率,即
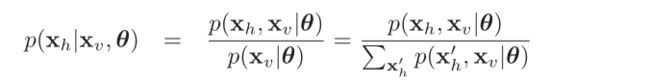
- 顺便提一点,在有些时候我们可能只关注隐变量中的一部分,这时候我们可以将隐变量再分为我们感兴趣的变量Xq(query variables)和我们不感兴趣的变量Xn(nuisance variables),我们可以通过边缘化Xn来计算Xq,即:
p ( x q ∣ x v , θ ) = ∑ x n p ( x q , x n ∣ x v , θ ) p({x_q}|{x_v},\theta ) = \sum\limits_{{x_n}} {p({x_q},{x_n}|{x_v},\theta )} p(xq∣xv,θ)=xn∑p(xq,xn∣xv,θ)
4. Learning
4.1 The difference between inference and learning
- Inference:计算隐变量得后验,假设参数θ是已知的。
- Learning:在给定Data情况下,通过极大后验概率估计(Maximum A Posteriori Estimation)来求解参数θ,即:
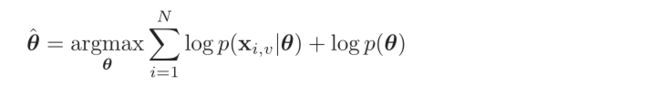
- 特别的,当θ的先验分布为均匀分布(uniform distribution),则MAP退化为MLE
4.2 The relationship between inference and learning
- 再贝叶斯学派中,万物皆概率,参数要被看成是未知的变量。因此从贝叶斯角度去看,inference和learning没有区别
- 因此,我们也可以将参数θ加入图模型中,然后推理出所有节点的值
4.3 Plate notation
- 当我们考虑数据中的参数时,我们经常假设样本独立同分布(iid),我们把独立同分布描述再图模型中可以这样表示,即:

其中,左边很明显,注意,这里的参数θ不在是常量而是一个变量,右边被成为“盘子”的表示法,一看就懂,不说了。
4.4 Learning from complete data
- 如果所有数据均被观测,即没有隐变量,我们说这样的数据为完备数据(complete data),这时对于整个数据集的似然函数为:

- 现在我们假设先验概率p(θ)也可以进行因子分解,即:

- 则我们可以把后验写出来,即:
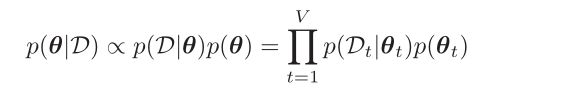
4.5 Learning with missing and/or latent variables
- EM算法你懂的
5. Conditional independence properties of DGMs(three properties)
5.1 D-separation(Global Markov Properties)
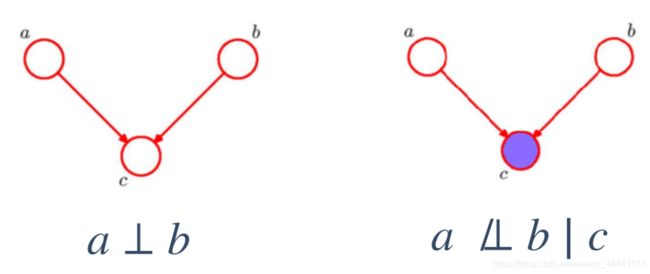
- 首先介绍三种贝叶斯网络的形式:
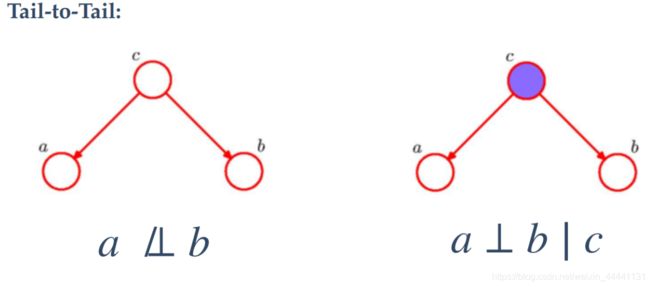
①tail-to-tail:
当c未观测时,a和b不独立;
当c被观测时,a和b独立.
②head-to-tail:
当c未观测时,a和b不独立;
当c被观测时,a和b独立.

③head-to-head:
当c未观测时,a和b独立;
当c被观测时,a和b不独立.
- D-separation(全局马尔科夫性质)
①D-separation是一种用来判断变量是否条件独立的图形化方法
②考虑一个一般的有向图,其中A,B,C是任意无交集的节点集合,我们希望弄清楚一个DAG是否暗示了一个特定的条件依赖来表述A⊥B|C。现在考虑从A这种任意节点到B中任意节点的所有路径(假设C被观测到,接③)
③我们说这样的路径被阻隔(Blocked),满足下面其一即可:
(1)A和B的 “head-to-tail” 和 “tail-to-tail”路径 都通过C
(2)A和B的 “head-to-head”不通过C及C的子孙
④若所有的路径均被阻隔,则有A⊥B|C.
5.2 Directed Local Markov Property
- 通过上述的D-separation,我们可以总结出一个公式:
t ⊥ n d ( t ) \ p a ( t ) ∣ p a ( t ) t \bot nd(t)\backslash pa(t)|pa(t) t⊥nd(t)\pa(t)∣pa(t)
t :任意节点
nd(t):non-descendant-除了它自己和自己的子孙的剩下所有节点
pa(t):t的父节点
描述为:给定某节点t的父节点,则该节点独立于他的祖先(不包括父节点)和与该节点没有关系的节点。
5.3 Ordered Markov Property
- 这是5.2性质的一个特例,我们来看一下,因为我们只看了节点t的先辈,很明显我们有这样的关系:pred(t)是nd(t)的子集
t ⊥ p r e d ( t ) \ p a ( t ) ∣ p a ( t ) t \bot pred(t)\backslash pa(t)|pa(t) t⊥pred(t)\pa(t)∣pa(t) - 举个栗子:pred(3)={1,2},pa(3)=1,则有3⊥2|1

5.4 The relationships among these properties
- 等价的,谁都可以推出谁!
- 另外别忘了有向图模型的一个很重要的性质:因子分解性质
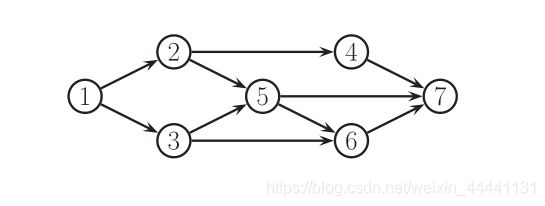
5.5 Markov blanket in DGM
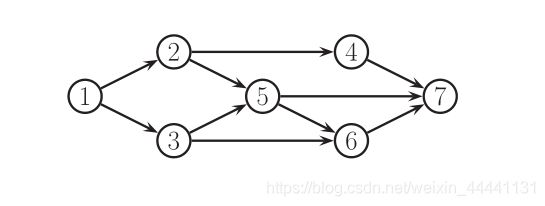
- 存在这样的节点集mb(t):使节点t独立于所有其他节点,则mb(t)节点集被称为节点t的马尔可夫毯子(Markov Blanket)
- 可以证明,一个节点的马尔可夫毯子等于其父亲节点、儿子节点、儿子节点的其他父亲(Co-parents),即
m b ( t ) ≜ c h ( t ) ∪ p a ( t ) ∪ c o p a ( t ) mb(t) \triangleq ch(t) \cup pa(t) \cup copa(t) mb(t)≜ch(t)∪pa(t)∪copa(t)
- 举个栗子:
m b ( 5 ) = { 6 , 7 } ∪ { 2 , 3 } ∪ { 4 } = { 2 , 3 , 4 , 6 , 7 } mb(5) = \{ 6,7\} \cup \{ 2,3\} \cup \{ 4\} = \{ 2,3,4,6,7\} mb(5)={6,7}∪{2,3}∪{4}={2,3,4,6,7}
6. Decision
- 这里不做说明了,就是将推断学习到的东西做出一些决策,例如朴素贝叶斯中判断样本属于哪一类.
参考文献
《Machine Learning - A Probabilistic Perspective》