DatawhaleX天池二手车Task4:建模与调参

XGBoost手推算法-贪心学院李文哲老师直播公开课笔记

讲座重点讲解XGBoost算法技术细节，从目标函数的构建、泰勒近似、树的参数化和树结构的构建，以下是听课记录参考公众号《ML学习总结》整理出的笔记。

将多个弱学习器模型组合在一起通常可以产生更强大的模型，这是集成模型的主要思路，集成模型有bagging，boosting，stacking等。以上Bagging的流程中，弱学习器相互独立训练，最终使用的加权平均或者投票来产生预测结果。

直观理解：
bagging是一群专家来回答问题；容易过拟合。
boosting是一群小学生来回答问题；容易欠拟合。
Bagging和Boosting的共同点：均是由多个弱的模型构成
区别：bagging包含过拟合的基类模型，基类模型训练时是并行的，boosting 包含欠拟合的基类模型，模型训练时串行的。
boosting算法的发展：adaboost, GBDT, xgboost, lightgbm, catboost，其中后三者目前较常使用，多用于各种比赛和工业界。


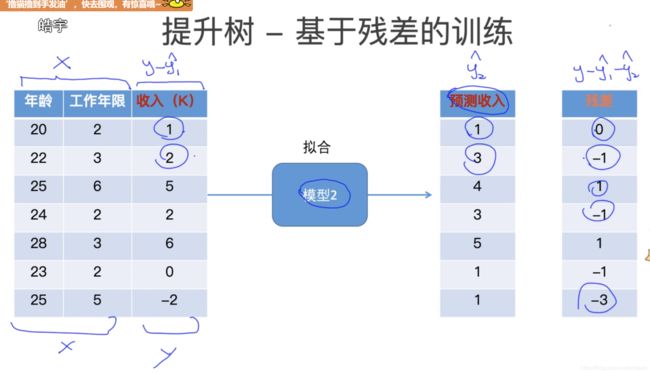
提升树-基于残差的训练
第一步，训练第一个模型，真实值与预测值存在差距（残差）；
第二步，第二个模型拟合第一个模型的残差，剩余的残差有减小的趋势；
第三步，第三个模型拟合第二个模型的残差（y-y1-y2），得到第三个模型的残差。
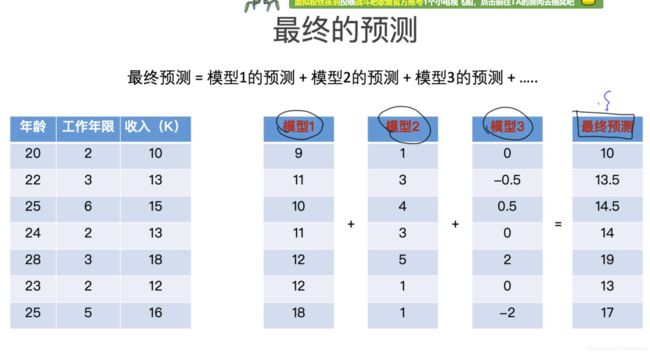
通过三个模型的拟合相加，得到最终的预测结果。

XGboost与随机森林的训练方式有很大区别，随机森林同时并行训练多个树模型，通过加权或投票的方式得到最终结果。

XGboost基于残差的提升方法，拟合上一步树模型的残差，串行地训练树模型，最终的结果是多个模型的预测结果相加得到最终结果。

(问题：boosting是串行构造树的方法，xgboost又有并行一说，并行是怎么操作的？

xgboost 模型的并行发生在每一个树的拟合中，每个节点都包含样本，特征数量很多时，树的生长非常最耗时，此时并行计算每个特征的增益，选择最佳分裂点。可以理解为一棵树从上到下展开，串行是从上到下的，并行是在水平层面的）


多个模型的拟合相加，得到最终的预测结果

目标函数的构建为损失函数和惩罚项的和，给每一棵树加上惩罚项，用惩罚项来控制树的复杂度。

树的复杂度：叶节点个数越多，树的深度地越深时，直观的感受是树模型越复杂。

叠加式训练：
当训练第k棵树的时候，前面的第1到k-1棵树都已经已知，第1棵树作为base case，y为所有树的累加值。将目标函数中的损失函数拆解，将复杂度函数也拆解分为常数项和未知项，隐去不影响目标函数obj的求解的常数项。当训练第k棵树的时候，最小化目标函数。

Taylor’s Expansion：
$f(x)=\frac{f\left(x_0\right)}{0!}+\frac{f^{\prime }\left(x_0\right)}{1!}\left(x-x_0\right)+\frac{f^{\prime \prime }\left(x_0\right)}{2!}{\left(x-x_0\right)}^2+\dots +\frac{f^{(n)}\left(x_0\right)}{n!}{\left(x-x_0\right)}^n+R_n(x)$

使用二阶泰勒公式来得到目标函数的近似表示，近似之后的obj中的已知信息和未知信息已经分离，得到关于fk(xi)的新的目标函数。

【注：xgboost 中泰勒二阶近似的优点：1.相比GBDT只利用一阶导信息，xgboost利用了二阶导信息，对损失函数的近似精度更高；2.便于自定义损失函数，只要满足这个损失函数可以求一阶和二阶导，也有利于后面的目标函数的极小值求解。】


重新定义一棵树：
1.w=(w1,w2,w3)分别为三个叶节点的权值(向量)
2.假定有5个样本，第1个和第3个样本落在了节点1，第4个样本落到了节点2，第2个和第5个样本落在了节点3上，用q(x)表示样本x的位置，参数w的下标仍是参数定义为q。
Ij表示第j个节点有哪些样本，会按照叶节点的位置重新组织样本得到集合。在下面重写obj时会使用Ij来将Wq两个参数W和q进行分离。

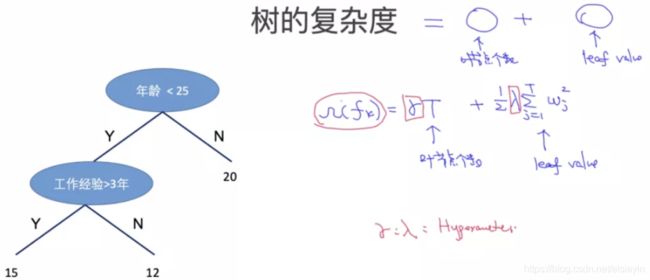
定义树的复杂度Ω：

叶子的节点数量T，叶子节点权值向量的组合，γ和λ为控制T和w的超参数。

将重新定义的树（Ij）和树的复杂度Ω代入之前的目标函数obj，其中对所有的训练样本，按照叶子节点进行了分组（j=1,2…T，T为叶子节点个数），obj现在变成关于Wj的一元二次函数，形如f(x)=aX^2+bX, 会在X=-b/2a处取得极小值，因此可得obj在w处取得极小值obj。


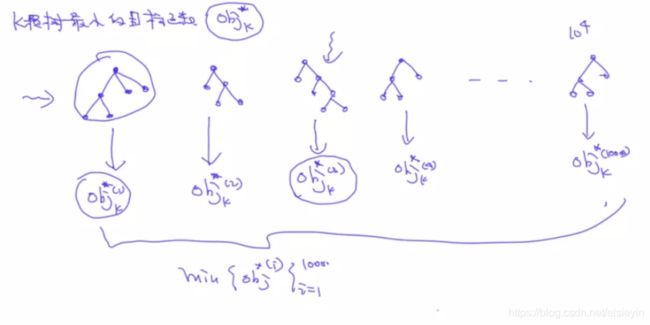
针对一棵形状固定的树，即按照特定分裂点分裂后的目标函数obj的极小值可以根据以上公式求出，如果穷举所有可能形状的树，比较所有树的obj, 理论上是可以得到obj最小的那棵树，但是实际情况树的数量为指数级，在有限的资源下穷举十分困难。因此考虑贪心算法的思路。

【注：贪心算法在对问题求解时，总是做出在当前看来是最好的选择，不考虑整体最优，所做出的是在某种意义上的局部最优解，贪心策略具备无后效性，即某个状态以前的过程不会影响以后的状态，只与当前状态有关】

树的分裂和生长：

假设现在已经生成一棵树，此时的目标函数obj(old)的极小值可以得出，接下来进行特征选择分配样本生成新的树时，可得到obj(new)的极小值，极大化obj(old)-obj(new)的差值，当差值最大时，意味着obj(new)取得所有情况下的极小值，此时可以确定本次分裂最优结构的树。

每次在上一次的预测基础上取最优进一步分裂特征并建树，不断重复这样的操作。

【注：树的生长停止条件：1.设置阈值,当分裂带来的增益小于设定阀值的时候，忽略分裂停止树生长；2.达到设置的树的最大深度时停止生长；3.叶子节点的样本权值低于某一阈值，表示树分裂的太细叶子节点过多会出现过拟合，停止生长。】

Kaggle开放日GBDT细节与实现

原理目前一知半解，但是代码，还在研究中，不是很懂
另外朋友推荐了一篇hyperopt的文章，但并不会用
https://www.jianshu.com/p/35eed1567463