Python数据结构——array

array 数组

array是什么

一般来说，array基本是所有程序语言都有的一种基础线性结构，元素以特定的顺序存储在一段连续的内存中。

在Python中其实也有array这种数据结构，和其他语言的array一样，也是内存连续，只能存储相同类型元素的线性数据结构，而且Python的array只能存储数值和字符。

array有哪些功能

这里只讲一下内置array。需要先import array:

    # 可以直接使用内置array
    from array import array
    # 或是从numpy中引用array
    import numpy as np
    np.array()

array的创建

    # 构造方法如下
    # 需要提供一个类型代码字符来指示存储何种元素
    # 以及一个可迭代对象来填充元素
    array.array(typecode[, initializer])
    
    # array所有的类型代码字符
    print(array.typecodes)
    bBuhHiIlLqQfd
    
    # 创建一个存储整型的array
    arr = array('i', [1,2,3,4,5,6])

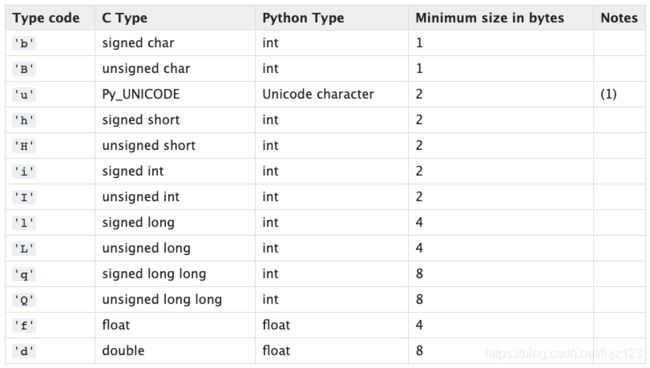
array类型代码

从Python类型来看，只能存储整数，浮点数和unicode字符

并且在Python中，最小的整型size为28个字节，整型的长度可变， 每增加$2^{30}$就增加4个字节。这点以后再补充。

array的方法和操作

这里暂且只谈一下数据结构比较基本的增删改查等操作, 更多代码详情见github

具体实现可参考此处

索引

下标索引

所有语言的array都可以通过下标来直接访问对象。

这一点是由计算机的硬件实现的。我们知道array的元素在内存上的分布是连续的，而且元素种类相同，所以数组中任意一项的地址可以由基本地址和偏移量算出。基本地址就是第一个元素的地址，偏移量就等于索引乘以数组内任意元素占用的内存大小。

时间复杂度：

因为每一次找到对应的元素只需要一次计算，所以索引的时间复杂度为$O(1)$

切片索引

array通过下表索引固然很方便，但有时我们想一次性获取更多的内容，此时可以使用切片索引。

array[i1:i2]可以返回一个新的数组，包含原数组索引为i1到i2-1的全部元素

时间复杂度：

切片索引的实际操作为：

    def slice(i1, i2):
      	res_arr = array(typecode)       # 先创建一个新的数组
      	for i in range(i1, i2):					# 然后按照索引依次读取原数组中的元素
        		val = arr[i]                
        		res_arr.append(val)         # 将这些元素添加到新的数组中
      	return res_arr

因此切片索引的时间复杂度为$O(2k)\Rightarrow O(k)$，$k$指的是参数的数量

增加元素

append()

array.append(x)可以直接在数组的末尾添加新元素

时间复杂度：

要想增加元素，我们必须先定位到最后一位元素的后一位，然后执行赋值操作

所以索引到最后一个元素和增加一个元素都只需要一次运算，时间复杂度为$O(1)$

insert()

insert(i, x)可以用来在索引i处添加元素x

时间复杂度：

要想在索引i插入某个元素，我们必须先将索引i及之后的元素向后移动一位，然后再给索引i赋值

因此插入元素时需要的后移操作的次数和数组内元素的个数有关，所以时间复杂度为$O(n)$

extend()

extend(iterable)操作将一个可迭代对象的每一个元素添加到数组末尾，如果数据类型和数组的数据类型不匹配会有TypeError异常

时间复杂度：

操作过程为先遍历读取可迭代对象的每个元素，然后添加到数组末尾，时间复杂度为$O(k)$

删除元素

pop()

pop(i=-1)用来移除数组中的某个元素并返回，可以传入索引值，默认为-1。也就是说pop()默认移除最后一位元素。

时间复杂度：

如果只是移除最后一位元素，那么时间复杂度为$O(1)$

如果移除的是数组中的元素，那么还需要进行数据前移，前移的次数也和数组大小有关，因此时间复杂度为$O(n)$

remove()

remove(x)操作可以移除x元素在数组中的第一个匹配项

时间复杂度：

remove(x)操作可以视为先查找再移除最后数据前移，而查找和数据前移都和数组的大小有关，所以时间复杂度为$O(n)$。但实际使用上，remove()的操作效率较低，因为同时执行了查找和数据前移操作。

修改元素

array的元素修改直接通过索引完成

时间复杂度：

如果是下标索引，时间复杂度为$O(1)$

如果是切片索引，时间复杂度为$O(k)$，可看成下标索引重复$k$次

查找元素

index()

index(x)操作可以返回元素x第一次出现的索引值，如果没找到会出现ValueError异常

时间复杂度：

为了查找特定元素，我们需要遍历数组，所以时间复杂度为$O(n)$

count()

count(x)操作可返回元素x在数组中出现的次数

时间复杂度：

同样的，需要遍历整个数组才能得到结果，所以时间复杂度为$O(n)$

array的优点和缺点

优点

1. 数组比列表更精简：Python数组跟C语言数组一样精简。创建数组需要一个类型码，这个类型码用来表示在底层的C语言应该存放怎样的数据类型。比如b类型码代表的是有符号的字符（signedchar），array(‘b’)创建出的数组就只能存放一个字节大小的整数，范围从-128到127，这样在序列很大的时候，我们能节省很多空间。
2. 数组提供更快的文件处理方法：另外，数组还提供从文件读取和存入文件的更快的方法，如.frombytes和.tofile。

缺点
3. 元素类型限制：使用时必须要限制元素类型
4. 不利于数据修改：插入和删除操作需要移动一系列元素。

---

相关章节

Python数据结构——array
Python数据结构——list
Python数据结构——tuple