CRF
参考文献
简明条件随机场CRF介绍 | 附带纯Keras实现
掌握动态规划,助你成为优秀的算法工程师
1. 逐帧 softmax 和 CRF 的异同
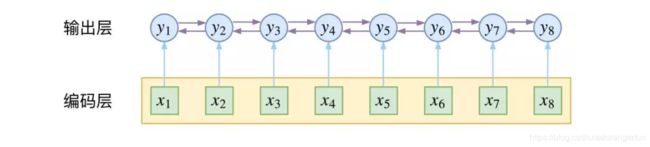
CRF 主要用于序列标注问题,可以简单理解为是给序列中的每一帧都进行分类,既然是分类,很自然想到将这个序列用 CNN 或者 RNN 进行编码后,接一个全连接层用 softmax 激活,如下图所示:

当我们设计标签时,比如用 s、b、m、e 的 4 个标签来做字标注法的分词,目标输出序列本身会带有一些上下文关联,比如 s 后面就不能接 m 和 e,等等。逐标签 softmax 并没有考虑这种输出层面的上下文关联,所以它意味着把这些关联放到了编码层面,希望模型能自己学到这些内容,但有时候会“强模型所难”。
而 CRF 则更直接一点,它将输出层面的关联分离了出来,这使得模型在学习上更为“从容”:
当然,如果仅仅是引入输出的关联,还不仅仅是 CRF 的全部,CRF 的真正精巧的地方,是它以路径为单位,考虑的是路径的概率。
2. CRF模型
假如一个输入有 n 帧,每一帧的标签有 k 种可能性,那么理论上就有 k n k^n kn z种不同的输入。我们可以将它用如下的网络图进行简单的可视化。在下图中,每个点代表一个标签的可能性,点之间的连线表示标签之间的关联,而每一种标注结果,都对应着图上的一条完整的路径。
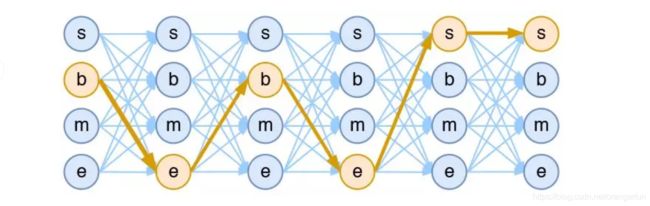
而在序列标注任务中,我们的正确答案是一般是唯一的。比如“今天天气不错”,如果对应的分词结果是“今天/天气/不/错”,那么目标输出序列就是bebess,除此之外别的路径都不符合要求。
换言之,在序列标注任务中,我们的研究的基本单位应该是路径,我们要做的事情,是从 k n k^n kn 条路径选出正确的一条,那就意味着,如果将它视为一个分类问题,那么将是 k n k^n kn 类中选一类的分类问题
这就是逐帧 softmax 和 CRF 的根本不同了:前者将序列标注看成是 n 个 k 分类问题,后者将序列标注看成是 1 个 k n k^n kn 分类问题
具体来讲,在 CRF 的序列标注问题中,我们要计算的是条件概率:
P ( y 1 , … , y n ∣ x 1 , … , x n ) = P ( y 1 , … , y n ∣ x ) , x = ( x 1 , … , x n ) P\left(y_{1}, \ldots, y_{n} \mid x_{1}, \ldots, x_{n}\right)=P\left(y_{1}, \ldots, y_{n} \mid x\right), \quad x=\left(x_{1}, \ldots, x_{n}\right) P(y1,…,yn∣x1,…,xn)=P(y1,…,yn∣x),x=(x1,…,xn)
为了得到这个概率的估计,CRF 做了两个假设:
(1)该分布是指数族分布
这个假设意味着存在函数 f ( y 1 , … , y n ; x ) f(y_1,…,y_n;x) f(y1,…,yn;x),使得:
P ( y 1 , … , y n ∣ x ) = 1 Z ( x ) exp ( f ( y 1 , … , y n ; x ) ) P\left(y_{1}, \ldots, y_{n} \mid \boldsymbol{x}\right)=\frac{1}{Z(\boldsymbol{x})} \exp \left(f\left(y_{1}, \ldots, y_{n} ; \boldsymbol{x}\right)\right) P(y1,…,yn∣x)=Z(x)1exp(f(y1,…,yn;x))
其中 Z ( x ) Z(x) Z(x) 是归一化因子,因为这个是条件分布,所以归一化因子跟 x 有关。这个 f f f 函数可以视为一个打分函数,打分函数取指数并归一化后就得到概率分布
(2)输出之间的关联仅发生在相邻位置,并且关联是指数加性的
这个假设意味着 f ( y 1 , … , y n ; x ) f(y_1,…,y_n;x) f(y1,…,yn;x) 可以更进一步简化为:
f ( y 1 , … , y n ; x ) = h ( y 1 ; x ) + g ( y 1 , y 2 ; x ) + h ( y 2 ; x ) + … + g ( y n − 1 , y n ; x ) + h ( y n ; x ) ( 3 ) \begin{aligned}f\left(y_{1}, \ldots, y_{n} ; \boldsymbol{x}\right)=h\left(y_{1} ; \boldsymbol{x}\right) &+g\left(y_{1}, y_{2} ; \boldsymbol{x}\right)+h\left(y_{2} ; \boldsymbol{x}\right)+\ldots &+g\left(y_{n-1}, y_{n} ; \boldsymbol{x}\right)+h\left(y_{n} ; \boldsymbol{x}\right) \end{aligned} \,\,\,\,\,\,\,\,(3) f(y1,…,yn;x)=h(y1;x)+g(y1,y2;x)+h(y2;x)+…+g(yn−1,yn;x)+h(yn;x)(3)
这也就是说,现在我们只需要对每一个标签和每一个相邻标签对分别打分,然后将所有打分结果求和得到总分。
线性链CRF
尽管已经做了大量简化,但一般来说,(3) 式所表示的概率模型还是过于复杂,难以求解。于是考虑到当前深度学习模型中,RNN 或者CNN 等模型已经能够比较充分捕捉各个 y 与输出 x 的联系,因此,我们不妨考虑函数 g 跟 x 无关,那么:
f ( y 1 , … , y n ; x ) = h ( y 1 ; x ) + g ( y 1 , y 2 ) + h ( y 2 ; x ) + … + g ( y n − 1 , y n ) + h ( y n ; x ) ( 4 ) \begin{aligned} f\left(y_{1}, \ldots, y_{n} ; \boldsymbol{x}\right)=h\left(y_{1} ; \boldsymbol{x}\right) &+g\left(y_{1}, y_{2}\right)+h\left(y_{2} ; \boldsymbol{x}\right)+\ldots &+g\left(y_{n-1}, y_{n}\right)+h\left(y_{n} ; \boldsymbol{x}\right) \end{aligned} \,\,\,\,\,\,\,\,(4) f(y1,…,yn;x)=h(y1;x)+g(y1,y2)+h(y2;x)+…+g(yn−1,yn)+h(yn;x)(4)
这时候 g g g 实际上就是一个有限的、待训练的参数矩阵而已,而单标签的打分函数 h ( y i ; x ) h(y_i;x) h(yi;x) 我们可以通过 RNN 或者 CNN 来建模。因此,该模型是可以建立的,其中概率分布变为:
P ( y 1 , … , y n ∣ x ) = 1 Z ( x ) exp ( h ( y 1 ; x ) + ∑ k = 1 n − 1 g ( y k , y k + 1 ) + h ( y k + 1 ; x ) ) P\left(y_{1}, \ldots, y_{n} \mid \boldsymbol{x}\right)=\frac{1}{Z(\boldsymbol{x})} \exp \left(h\left(y_{1} ; \boldsymbol{x}\right)+\sum_{k=1}^{n-1} g\left(y_{k}, y_{k+1}\right)+h\left(y_{k+1} ; \boldsymbol{x}\right)\right) P(y1,…,yn∣x)=Z(x)1exp(h(y1;x)+k=1∑n−1g(yk,yk+1)+h(yk+1;x))
上面就是线性链的概念
归一化因子
为了训练 CRF 模型,我们用最大似然方法,也就是用
− log P ( y 1 , … , y n ∣ x ) -\log P\left(y_{1}, \ldots, y_{n} \mid x\right) −logP(y1,…,yn∣x)
作为损失函数,可以算出它等于:
− ( h ( y 1 ; x ) + ∑ k = 1 n − 1 g ( y k , y k + 1 ) + h ( y k + 1 ; x ) ) + log Z ( x ) -\left(h\left(y_{1} ; x\right)+\sum_{k=1}^{n-1} g\left(y_{k}, y_{k+1}\right)+h\left(y_{k+1} ; x\right)\right)+\log Z(x) −(h(y1;x)+k=1∑n−1g(yk,yk+1)+h(yk+1;x))+logZ(x)
其中第一项是原来概率式的分子的对数,它目标的序列的打分,虽然它看上去挺迂回的,但是并不难计算。真正的难度在于分母的对数 l o g Z ( x ) logZ(x) logZ(x) 这一项。
归一化因子,在物理上也叫配分函数,在这里它需要我们对所有可能的路径的打分进行指数求和,而我们前面已经说到,这样的路径数是指数量级的 ( k n ) (k^n) (kn),因此直接来算几乎是不可能的
事实上,归一化因子难算,几乎是所有概率图模型的公共难题。幸运的是,在 CRF 模型中,由于我们只考虑了临近标签的联系(马尔可夫假设),因此我们可以递归地算出归一化因子,这使得原来是指数级的计算量降低为线性级别
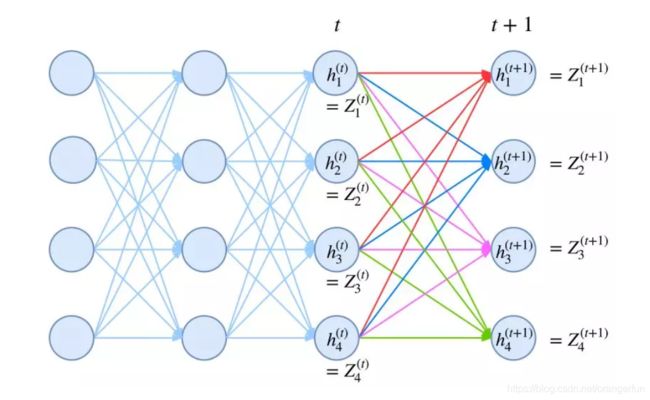
具体来说,我们将计算到时刻 t t t 的归一化因子记为 Z t Z_t Zt,并将它分为 k k k 个部分:
Z t = Z t ( 1 ) + Z t ( 2 ) + ⋯ + Z t ( k ) Z_{t}=Z_{t}^{(1)}+Z_{t}^{(2)}+\cdots+Z_{t}^{(k)} Zt=Zt(1)+Zt(2)+⋯+Zt(k)
其中 Z t ( 1 ) , … , Z t ( k ) Z_{t}^{(1)}, \ldots, Z_{t}^{(k)} Zt(1),…,Zt(k) 分别是截止到当前时刻 t t t 、以标签 1 , … , k 1,…,k 1,…,k 为终点的所有路径的得分指数和。那么,我们可以递归地计算:
Z t + 1 ( 1 ) = ( Z t ( 1 ) G 11 + Z t ( 2 ) G 21 + ⋯ + Z t ( k ) G k 1 ) h t + 1 ( 1 ∣ x ) Z t + 1 ( 2 ) = ( Z t ( 1 ) G 12 + Z t ( 2 ) G 22 + ⋯ + Z t ( k ) G k 2 ) h t + 1 ( 2 ∣ x ) Z t + 1 ( k ) = ( Z t ( 1 ) G 1 k + Z t ( 2 ) G 2 k + ⋯ + Z t ( k ) G k k ) h t + 1 ( k ∣ x ) \begin{array}{l} Z_{t+1}^{(1)}=\left(Z_{t}^{(1)} G_{11}+Z_{t}^{(2)} G_{21}+\cdots+Z_{t}^{(k)} G_{k 1}\right) h_{t+1}(1 \mid x) \\ Z_{t+1}^{(2)}=\left(Z_{t}^{(1)} G_{12}+Z_{t}^{(2)} G_{22}+\cdots+Z_{t}^{(k)} G_{k 2}\right) h_{t+1}(2 \mid x) \\ Z_{t+1}^{(k)}=\left(Z_{t}^{(1)} G_{1 k}+Z_{t}^{(2)} G_{2 k}+\cdots+Z_{t}^{(k)} G_{k k}\right) h_{t+1}(k \mid x) \end{array} Zt+1(1)=(Zt(1)G11+Zt(2)G21+⋯+Zt(k)Gk1)ht+1(1∣x)Zt+1(2)=(Zt(1)G12+Zt(2)G22+⋯+Zt(k)Gk2)ht+1(2∣x)Zt+1(k)=(Zt(1)G1k+Zt(2)G2k+⋯+Zt(k)Gkk)ht+1(k∣x)
它可以简单写为矩阵形式:
Z t + 1 = Z t G ⊗ H ( y t + 1 ∣ x ) ( 10 ) Z_{t+1}=Z_{t} G \otimes H\left(y_{t+1} \mid x\right) \,\,\,\,\,\,(10) Zt+1=ZtG⊗H(yt+1∣x)(10)
其中 Z t = [ Z t ( 1 ) , … , Z t ( k ) ] Z_{t}=\left[Z_{t}^{(1)}, \ldots, Z_{t}^{(k)}\right] Zt=[Zt(1),…,Zt(k)],而 G G G 是对 g ( y i , y j ) g(y_i,y_j) g(yi,yj) 各个元素取指数后的矩阵,即 G = e g ( y i , y j ) G=e^{g(y_i, y_j)} G=eg(yi,yj);而 H ( y t + 1 ∣ x ) H\left(y_{t+1} \mid x\right) H(yt+1∣x) 是编码模型 h ( y t + 1 ∣ x ) h\left(y_{t+1} \mid x\right) h(yt+1∣x)(RNN、CNN等)对位置 t + 1 t+1 t+1 的各个标签的打分的指数,即 H ( y t + 1 ∣ x ) = e h ( y t + 1 ∣ x ) H\left(y_{t+1} \mid x\right)=e^{h\left(y_{t+1} \mid x\right)} H(yt+1∣x)=eh(yt+1∣x),也是一个向量。式 (10) 中, Z t G Z_tG ZtG 这一步是矩阵乘法,得到一个向量,而 ⊗ 是两个向量的逐位对应相乘
3. CRF解码
写出损失函数 − l o g P ( y 1 , … , y n ∣ x ) −logP(y_1,…,y_n|x) −logP(y1,…,yn∣x) 后,就可以完成模型的训练了,因为目前的深度学习框架都已经带有自动求导的功能,只要我们能写出可导的 loss,就可以帮我们完成优化过程了
那么剩下的最后一步,就是模型训练完成后,如何根据输入找出最优路径来。跟前面一样,这也是一个从 k n k^n kn 条路径中选最优的问题,而同样地,因为马尔可夫假设的存在,它可以转化为一个动态规划问题,用 viterbi 算法解决,计算量正比于 n n n
维特比算法
维特比算法在自然语言处理中,像分词、词性标注、命名实体识别、输入法等等任务中都有非常重要的应用。
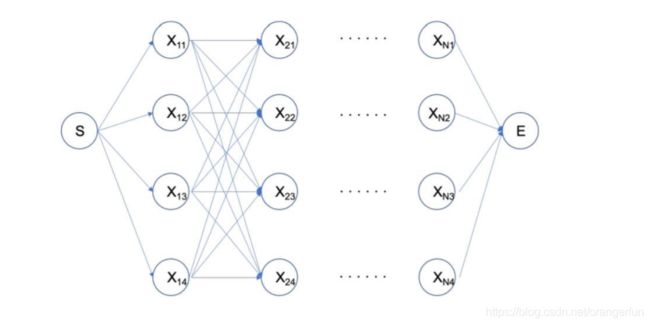
除了前面介绍的计算两个序列之间的距离以外,动态规划还有一个重要的应用场景,就是计算有向无环图(DAG)中两个节点间的最短路径,而维特比算法就是针对篱笆网络(Lattice Network)这一特殊的有向无环图而提出的
如上图所示,这是一个部分的篱笆网络,中间我们假设有 N N N 列,每列有 4 个节点,节点之间的权重我们暂时忽略。这个时候,网络的最左边有一个节点为 S S S,最右端有一个节点为 E E E。如果我想求 S S S 到 E E E 之间的最短路径,理所当然,我们如果穷举出所有的路径进行比较,也就是 4 N 4^N 4N 条路径,自然可以得到结果,但如果层数很多或者每层的节点数很多的时候,这种方法就显得不够友好了。
既然穷举法太过暴力,自然我们想试试能不能用动态规划来解决。首先,篱笆网络有这么一个特点,就是假设我们从第一列走到最后一列,我们一定会经过其中的第 i i i 时刻的某个节点。这个当然是显而易见的,但给我们带来了一个好处,那就是当我们计算最终的最短路径时,假设第 i i i 列有 k k k 个节点,如果我们已经计算了从开头到第 i i i 列所有 k k k 个节点的最短路径,那最终的最短路径一定是经过其中之一。第二,如果说最短路径 P P P 经过某个节点 x i j x_{ij} xij,那么从起始节点 S S S 到节点 x i j x_{ij} xij 的这段子路径 Q Q Q,一定是从起始节点 S S S 到 x i j x_{ij} xij 的最短路径,否则总路径 P P P 也不再是最短路径,这就自相矛盾了
有了这两个特性,终于可以试试动态规划了。同样我们从最左边的 S S S 节点出发,到第1列的4个节点,因为各只有一段距离,那自然这4个距离 d ( S , x 1 i ) d(S, x_{1i}) d(S,x1i) 为 S S S 节点到这4个节点的最短距离。当我们走到第2列时,根据之前的特性,一定会经过第1列的某个节点。此时的 S S S 节点到第2列某个节点的距离则为 d ( S , x 2 j ) = d ( S , x 1 i ) + d ( x 1 i , x 2 j ) d(S, x_{2j})=d(S, x_{1i}) + d(x_{1i}, x_{2j}) d(S,x2j)=d(S,x1i)+d(x1i,x2j)。而第1列有4个节点,所以 d ( S , x 2 j ) d(S, x_{2j}) d(S,x2j)应该是取4个距离中的最小值,当然在这一过程中,我们计算了4次,对于第2列的每个节点,我们都去进行如上的计算。所以在从第1列走到第2列的过程中,我们计算了4×4次,更关键的是我们把 d ( S , x 2 j ) d(S, x_{2j}) d(S,x2j)都要保存下来,作为我们下一次计算的基础。
而这个保存中间结果的过程,很明显地体现出了前文所述的动态规划的特点。接下来,我们继续走到第3列,同样的, S S S 节点到第3列某个节点的距离为 d ( S , x 3 k ) = d ( S , x 2 j ) + d ( x 2 j , x 3 k ) d(S, x_{3k})=d(S, x_{2j}) + d(x_{2j}, x_{3k}) d(S,x3k)=d(S,x2j)+d(x2j,x3k)。这个时候我们发现,等式右边的第一项,可以直接取我们刚刚保存的中间结果。对于 d ( S , x 3 k ) d(S, x_{3k}) d(S,x3k),我们依然是计算4次,取最小值保存下来。同样,需要遍历第3列的4个节点,所以又是4×4次计算。也就是说,每往前走1列,我们就计算了4×4次。以此类推,到最右边的节点 E E E的时候,我们需要计算 N × 4 2 N×4^2 N×42次,相比于穷举法的 4 N 4N 4N 条路径,这个效率已经是非常大的进步,把指数级的复杂度降低到了多项式级别
reference
简明条件随机场CRF介绍 | 附带纯Keras实现
掌握动态规划,助你成为优秀的算法工程师