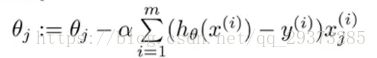吴恩达机器学习笔记--逻辑回归
逻辑回归（logistic regression）
分类（Classification)
分类问题举例：
邮件：垃圾邮件/非垃圾邮件？
在线交易：是否欺诈（是/否）？
肿瘤：恶性/良性？
以上问题可以称之为二分类问题，我们将因变量(dependant variable)可能属于的两个类分别称为负向类（negative class）和正向类（positive class），则因变量yϵ{0,1}，其中0表示负向类，1表示正向类。
对于多分类问题，可以如下定义因变量y：y∈{0,1,2,3,...,n}
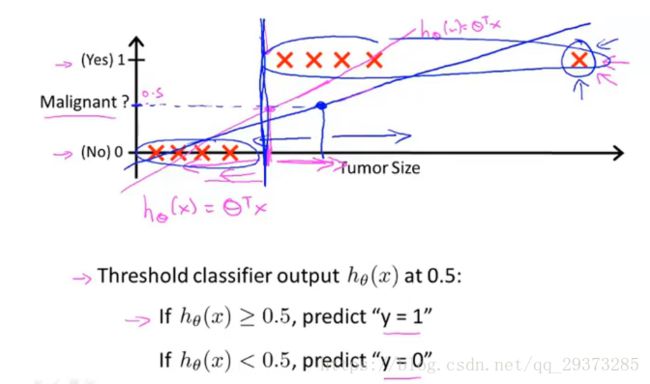
如果分类器用的是回归模型，并且已经训练好了一个模型，可以设置一个阈值：
如果hθ(x)≥0.5，则预测y=1,既y属于正例；
如果hθ(x)<0.5，则预测y=0,既y属于负例；
但是对于二分类问题来说，线性回归模型的Hypothesis输出值hθ(x)可以大于1也可以小于0。这个时候我们引出逻辑回归，逻辑回归的Hypothesis输出介于0与1之间，即:
0≤hθ(x)≤1
上图显示把线性回归用到分类问题中不是一个好主意
假说表示（Hypothesis Representation）
上一节谈到，我们需要将Hypothesis的输出界定在0和1之间，既：0≤hθ(x)≤1
但是线性回归无法做到，这里我们引入一个函数g, 令逻辑回归的Hypothesis表示为：
hθ(x)=g(θTx)，这里g称为Logistic function
例如，如果对于给定的 x，通过已经确定的参数计算得出 hθ(x)=0.7，则表示有 70%的几率y为正向类，相应地y为负向类的几率为 1-0.7=0.3。
Decision Boundary（决策边界）
现在假设我们有一个模型：
，并且参数θ是向量[-3 1 1]。则当-3+x1+x2 大于等于0，即x1+x2大于等于3 时，模型将预测 y=1。
我们可以绘制直线 x1+x2=3，这条线便是我们模型的分界线，将预测为 1 的区域和预测为 0 的区域分隔开。
上述只是一个线性的决策边界，当hθ(x)更复杂的时候，我们可以得到非线性的决策边界，例如：
Costfunction(代价函数)
对于线性回归模型，我们定义的代价函数是所有模型误差的平方和。理论上来说，我们也可以对逻辑回归模型沿用这个定义，但是问题在于，当我们将
带入到这样定义了的代价函数中时，我们得到的代价函数将是一个非凸函数（non-convex function）。
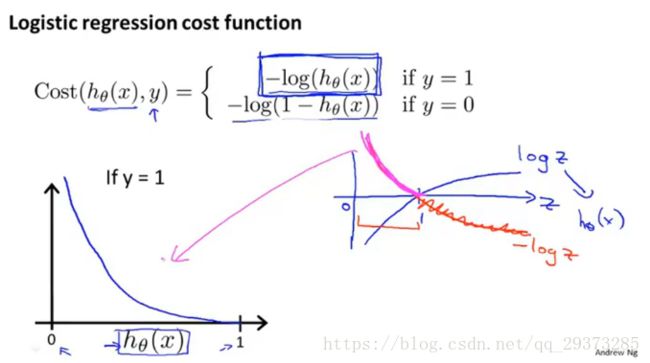
这意味着我们的代价函数有许多局部最小值，这将影响梯度下降算法寻找全局最小值。因此我们重新定义逻辑回归的代价函数： hθ：预测值 J(θ) ：代价函数 Cost(hθ(x).y)：重新定义的代价函数 <------会给我们带来一个凸优化的J(θ)，并且没有局部最优值
这样构建的Cost(hθ(x),y)函数的特点是：当实际的 y=1 且 hθ也为 1时误差为 0，当 y=1 但hθ不为1 时误差随着 hθ 的变小而变大；当实际的 y=0 且 hθ也为 0 时代价为0，当y=0 但hθ不为0时误差随着hθ的变大而变大。
_______________________________________________________________________________________________
logistic回归模型的代价函数 （解决二分类问题）
可以根据Cost(hθ(x).y)写成如下形式：
在得到这样一个代价函数以后，我们便可以用梯度下降算法**来求得能使代价函数最小的参数了。算法为：
也可以写成
*注意，这个算法和线性回归里的梯度下降算法几乎是一致的，除了hθ(x)的表示不同，所以实际上是两个不同的东西。
除了梯度下降算法以外，还有一些常被用来令代价函数最小的算法，这些算法更加复杂和优越，而且通常不需要人工选择学习率，通常比梯度下降算法要更加快速。这些算法有：共轭梯度（Conjugate Gradient），局部优化法(Broyden fletcher goldfarb shann,BFGS)和有限内存局部优化法(LBFGS)。
如何使用这些算法？
多个特征：
Multi-classclassification: One-vs-all(多类分类问题)
多类分类问题举例：
电子邮件分类/标注： 工作邮件，朋友邮件，家庭邮件，爱好邮件
医疗图表(medicaldiagrams): 没有生病，着凉，流感
天气：晴天，多云，雨，雪
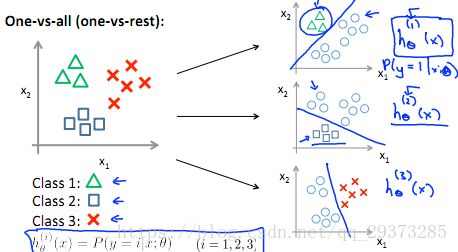
One-vs-all(one-vs-rest):
对于多类分类问题，可以将其看做成二类分类问题：保留其中的一类，剩下的作为另一类。例如，对于下面这个例子，可以分别计算其中一类相对于其他类的概率：
