从零开始深度学习0616——pytorch入门之GAN+dynamic torch+GPU(cuda)+dropout+BN

#-------------------------------conditional GAN-----------------
###################################################################################################################################

 

参考百度百科

https://baike.baidu.com/item/Gan/22181905?fr=aladdin

 

GAN 基本简介

模型通过框架中（至少）两个模块：生成模型（Generative Model）和判别模型（Discriminative Model）的互相博弈学习产生相当好的输出。原始 GAN 理论中，并不要求 G 和 D 都是神经网络，只需要是能拟合相应生成和判别的函数即可。但实用中一般均使用深度神经网络作为 G 和 D 。一个优秀的GAN应用需要有良好的训练方法，否则可能由于神经网络模型的自由性而导致输出不理想。

 

机器学习的模型可大体分为两类，生成模型（Generative Model）和判别模型（Discriminative Model）。判别模型需要输入变量 ，通过某种模型来预测 。生成模型是给定某种隐含信息，来随机产生观测数据。举个简单的例子，

• 判别模型：给定一张图，判断这张图里的动物是猫还是狗
• 生成模型：给一系列猫的图片，生成一张新的猫咪（不在数据集里）

对于判别模型，损失函数是容易定义的，因为输出的目标相对简单。但对于生成模型，损失函数的定义就不是那么容易。我们对于生成结果的期望，往往是一个暧昧不清，难以数学公理化定义的范式。所以不妨把生成模型的回馈部分，交给判别模型处理。这就是Goodfellow他将机器学习中的两大类模型，Generative和Discrimitive给紧密地联合在了一起  。

GAN的基本原理其实非常简单，这里以生成图片为例进行说明。假设我们有两个网络，G（Generator）和D（Discriminator）。正如它的名字所暗示的那样，它们的功能分别是：

• G是一个生成图片的网络，它接收一个随机的噪声z，通过这个噪声生成图片，记做G(z)。
• D是一个判别网络，判别一张图片是不是“真实的”。它的输入参数是x，x代表一张图片，输出D（x）代表x为真实图片的概率，如果为1，就代表100%是真实的图片，而输出为0，就代表不可能是真实的图片。

在训练过程中，生成网络G的目标就是尽量生成真实的图片去欺骗判别网络D。而D的目标就是尽量把G生成的图片和真实的图片分别开来。这样，G和D构成了一个动态的“博弈过程”。

最后博弈的结果是什么？在最理想的状态下，G可以生成足以“以假乱真”的图片G(z)。对于D来说，它难以判定G生成的图片究竟是不是真实的，因此D(G(z)) = 0.5。

这样我们的目的就达成了：我们得到了一个生成式的模型G，它可以用来生成图片。 

 

 

主要应用：

图像生成，如超分辨率任务，语义分割  图像翻译，卡通人物生成，人体姿态生成，年龄变换，风格变换

图像增强

 

…….

 

GAN 损失函数的理解

https://www.jianshu.com/p/588318e69eae

https://www.cnblogs.com/walter-xh/p/10051634.html

 

主要做到minG和maxD。

相互博弈产生良性结果

 

 

完整代码：

在上下区间中，迭代10000次，通过输入随机点，在上下蓝红曲线中，生成曲线

 

 

import torch

import torch.nn as nn

import numpy as np

import matplotlib.pyplot as plt



# torch.manual_seed(1)    # reproducible

# np.random.seed(1)



# Hyper Parameters

BATCH_SIZE = 64

LR_G = 0.0001           # learning rate for generator

LR_D = 0.0001           # learning rate for discriminator

N_IDEAS = 5             # think of this as number of ideas for generating an art work (Generator)

ART_COMPONENTS = 15     # it could be total point G can draw in the canvas

PAINT_POINTS = np.vstack([np.linspace(-1, 1, ART_COMPONENTS) for _ in range(BATCH_SIZE)])



# show our beautiful painting range

plt.plot(PAINT_POINTS[0], 2 * np.power(PAINT_POINTS[0], 2) + 1, c='#74BCFF', lw=3, label='upper bound')

plt.plot(PAINT_POINTS[0], 1 * np.power(PAINT_POINTS[0], 2) + 0, c='#FF9359', lw=3, label='lower bound')

plt.legend(loc='upper right')

plt.show()





def artist_works_with_labels():     # painting from the famous artist (real target)

    a = np.random.uniform(1, 2, size=BATCH_SIZE)[:, np.newaxis]

    paintings = a * np.power(PAINT_POINTS, 2) + (a-1)

    labels = (a-1) > 0.5            # upper paintings (1), lower paintings (0), two classes

    paintings = torch.from_numpy(paintings).float()

    labels = torch.from_numpy(labels.astype(np.float32))

    return paintings, labels





G = nn.Sequential(                      # Generator

    nn.Linear(N_IDEAS+1, 128),          # random ideas (could from normal distribution) + class label

    nn.ReLU(),

    nn.Linear(128, ART_COMPONENTS),     # making a painting from these random ideas

)



D = nn.Sequential(                      # Discriminator

    nn.Linear(ART_COMPONENTS+1, 128),   # receive art work either from the famous artist or a newbie like G with label

    nn.ReLU(),

    nn.Linear(128, 1),

    nn.Sigmoid(),                       # tell the probability that the art work is made by artist

)



opt_D = torch.optim.Adam(D.parameters(), lr=LR_D)

opt_G = torch.optim.Adam(G.parameters(), lr=LR_G)



plt.ion()   # something about continuous plotting



for step in range(10000):

    artist_paintings, labels = artist_works_with_labels()           # real painting, label from artist  真实的数据和标签



    G_ideas = torch.randn(BATCH_SIZE, N_IDEAS)                      # random ideas 随机在纵坐标生成BATCH_SIZE个数据   在横坐标生成N_IDEAS个数据

    G_inputs = torch.cat((G_ideas, labels), 1)                      # ideas with labels   将生成的数据和真实标签按行拼接

    G_paintings = G(G_inputs)                                       # fake painting w.r.t label from G  将假的拼接好的数据 输入到生成器



    D_inputs0 = torch.cat((artist_paintings, labels), 1)            # all have their labels   真实的数据和标签

    D_inputs1 = torch.cat((G_paintings, labels), 1)                 # 生成的数据和标签

    prob_artist0 = D(D_inputs0)                 # D try to increase  this prob  真实数据和标签输入到判别器

    prob_artist1 = D(D_inputs1)                 # D try to reduce this prob     生成的数据和标签输入到判别器



    D_score0 = torch.log(prob_artist0)          # maximise this for D  真实的数据的判别器的得分

    D_score1 = torch.log(1. - prob_artist1)     # maximise this for D  生成的数据的判别器的得分

    D_loss = - torch.mean(D_score0 + D_score1)  # minimise the negative of both two above for D  定义三重态损失函数 为了使损失函数小，就迫使prob_artist0 越大，prob_artist1越小

    G_loss = torch.mean(D_score1)               # minimise D score w.r.t G  生成器损失函数  只对生成的数据



    opt_D.zero_grad()

    D_loss.backward(retain_graph=True)      # reusing computational graph  保留参数  留给下次反向传播

    opt_D.step()



    opt_G.zero_grad()

    G_loss.backward()

    opt_G.step()



    if step % 200 == 0:  # plotting

        plt.cla()

        plt.plot(PAINT_POINTS[0], G_paintings.data.numpy()[0], c='#4AD631', lw=3, label='Generated painting',)

        bound = [0, 0.5] if labels.data[0, 0] == 0 else [0.5, 1]

        plt.plot(PAINT_POINTS[0], 2 * np.power(PAINT_POINTS[0], 2) + bound[1], c='#74BCFF', lw=3, label='upper bound')

        plt.plot(PAINT_POINTS[0], 1 * np.power(PAINT_POINTS[0], 2) + bound[0], c='#FF9359', lw=3, label='lower bound')

        plt.text(-.5, 2.3, 'D accuracy=%.2f (0.5 for D to converge)' % prob_artist0.data.numpy().mean(), fontdict={'size': 13})

        plt.text(-.5, 2, 'D score= %.2f (-1.38 for G to converge)' % -D_loss.data.numpy(), fontdict={'size': 13})

        plt.text(-.5, 1.7, 'Class = %i' % int(labels.data[0, 0]), fontdict={'size': 13})

        plt.ylim((0, 3));plt.legend(loc='upper right', fontsize=10);plt.draw();plt.pause(0.1)



plt.ioff()

plt.show()



# plot a generated painting for upper class

z = torch.randn(1, N_IDEAS)

label = torch.FloatTensor([[1.]])     # for upper class

G_inputs = torch.cat((z, label), 1)

G_paintings = G(G_inputs)

plt.plot(PAINT_POINTS[0], G_paintings.data.numpy()[0], c='#4AD631', lw=3, label='G painting for upper class',)

plt.plot(PAINT_POINTS[0], 2 * np.power(PAINT_POINTS[0], 2) + bound[1], c='#74BCFF', lw=3, label='upper bound (class 1)')

plt.plot(PAINT_POINTS[0], 1 * np.power(PAINT_POINTS[0], 2) + bound[0], c='#FF9359', lw=3, label='lower bound (class 1)')

plt.ylim((0, 3));plt.legend(loc='upper right', fontsize=10);plt.show()

 

 

运行结果：

 

 

 

--------------------------------------为什么torch是动态的--------------------------------------------------

##############################################################################################################################################

 

 

与tensorflow 不同  

Tensorflow 是静态的编辑器，先建立好一个静态的图表，然后再把数据放到图表中进行计算，然后再反向传递更新这些参数

 

因为在某些实际情况可能batch_size  和 time_step 是不确定的  

但是又不能两个同时不确定  这时程序会报错

 

 

例子使用RNN的time_step 随机来实现

 

 

完整代码：

 

import torch

from torch import nn

import numpy as np

import matplotlib.pyplot as plt



# torch.manual_seed(1)    # reproducible



# Hyper Parameters

INPUT_SIZE = 1          # rnn input size / image width

LR = 0.02               # learning rate





class RNN(nn.Module):

    def __init__(self):

        super(RNN, self).__init__()



        self.rnn = nn.RNN(

            input_size=1,

            hidden_size=32,     # rnn hidden unit

            num_layers=1,       # number of rnn layer

            batch_first=True,   # input & output will has batch size as 1s dimension. e.g. (batch, time_step, input_size)

        )

        self.out = nn.Linear(32, 1)



    def forward(self, x, h_state):

        # x (batch, time_step, input_size)

        # h_state (n_layers, batch, hidden_size)

        # r_out (batch, time_step, output_size)

        r_out, h_state = self.rnn(x, h_state)



        outs = []                                   # this is where you can find torch is dynamic

        for time_step in range(r_out.size(1)):      # calculate output for each time step

            outs.append(self.out(r_out[:, time_step, :]))

        return torch.stack(outs, dim=1), h_state





rnn = RNN()

print(rnn)



optimizer = torch.optim.Adam(rnn.parameters(), lr=LR)   # optimize all cnn parameters

loss_func = nn.MSELoss()                                # the target label is not one-hotted



h_state = None   # for initial hidden state



plt.figure(1, figsize=(12, 5))

plt.ion()   # continuously plot



########################  Below is different #########################



################ static time steps ##########

# for step in range(60):

#     start, end = step * np.pi, (step+1)*np.pi   # time steps

#     # use sin predicts cos

#     steps = np.linspace(start, end, 10, dtype=np.float32)



################ dynamic time steps #########

step = 0

for i in range(60):

    dynamic_steps = np.random.randint(1, 4)  # has random time steps  随机步长 动态化 使每次输入的步长都是不一样的

    start, end = step * np.pi, (step + dynamic_steps) * np.pi  # different time steps length

    step += dynamic_steps



    # use sin predicts cos

    steps = np.linspace(start, end, 10 * dynamic_steps, dtype=np.float32)



#######################  Above is different ###########################



    print(len(steps))       # print how many time step feed to RNN



    x_np = np.sin(steps)    # float32 for converting torch FloatTensor

    y_np = np.cos(steps)



    x = torch.from_numpy(x_np[np.newaxis, :, np.newaxis])    # shape (batch, time_step, input_size)

    y = torch.from_numpy(y_np[np.newaxis, :, np.newaxis])



    prediction, h_state = rnn(x, h_state)   # rnn output

    # !! next step is important !!

    h_state = h_state.data        # repack the hidden state, break the connection from last iteration



    loss = loss_func(prediction, y)         # cross entropy loss

    optimizer.zero_grad()                   # clear gradients for this training step

    loss.backward()                         # backpropagation, compute gradients

    optimizer.step()                        # apply gradients



    # plotting

    plt.plot(steps, y_np.flatten(), 'r-')

    plt.plot(steps, prediction.data.numpy().flatten(), 'b-')

    plt.draw()

    plt.pause(0.05)



plt.ioff()

plt.show()

 

 

运行结果：

 

 

 

 

---------------------------------------------GPU-----------------------------------------------------------------

###########################################################################################################################################

 

套用之前CNN实现数字识别的代码

简单加上几个方法

对训练数据 网络模型等  加上.cuda()  的方法  

 

import torch

import torch.nn as nn

import torch.utils.data as Data

import torchvision



# torch.manual_seed(1)



EPOCH = 1

BATCH_SIZE = 50

LR = 0.001

DOWNLOAD_MNIST = False



train_data = torchvision.datasets.MNIST(root='./mnist/', train=True, transform=torchvision.transforms.ToTensor(), download=DOWNLOAD_MNIST,)

train_loader = Data.DataLoader(dataset=train_data, batch_size=BATCH_SIZE, shuffle=True)



test_data = torchvision.datasets.MNIST(root='./mnist/', train=False)



# !!!!!!!! Change in here !!!!!!!!! #

test_x = torch.unsqueeze(test_data.test_data, dim=1).type(torch.FloatTensor)[:2000].cuda()/255.   # Tensor on GPU

test_y = test_data.test_labels[:2000].cuda()





class CNN(nn.Module):

    def __init__(self):

        super(CNN, self).__init__()

        self.conv1 = nn.Sequential(nn.Conv2d(in_channels=1, out_channels=16, kernel_size=5, stride=1, padding=2,),

                                   nn.ReLU(), nn.MaxPool2d(kernel_size=2),)

        self.conv2 = nn.Sequential(nn.Conv2d(16, 32, 5, 1, 2), nn.ReLU(), nn.MaxPool2d(2),)

        self.out = nn.Linear(32 * 7 * 7, 10)



    def forward(self, x):

        x = self.conv1(x)

        x = self.conv2(x)

        x = x.view(x.size(0), -1)

        output = self.out(x)

        return output



cnn = CNN()



# !!!!!!!! Change in here !!!!!!!!! #

cnn.cuda()      # Moves all model parameters and buffers to the GPU.



optimizer = torch.optim.Adam(cnn.parameters(), lr=LR)

loss_func = nn.CrossEntropyLoss()



for epoch in range(EPOCH):

    for step, (x, y) in enumerate(train_loader):



        # !!!!!!!! Change in here !!!!!!!!! #

        b_x = x.cuda()    # Tensor on GPU

        b_y = y.cuda()    # Tensor on GPU



        output = cnn(b_x)

        loss = loss_func(output, b_y)

        optimizer.zero_grad()

        loss.backward()

        optimizer.step()



        if step % 50 == 0:

            test_output = cnn(test_x)



            # !!!!!!!! Change in here !!!!!!!!! #

            pred_y = torch.max(test_output, 1)[1].cuda().data  # move the computation in GPU



            accuracy = torch.sum(pred_y == test_y).type(torch.FloatTensor) / test_y.size(0)

            print('Epoch: ', epoch, '| train loss: %.4f' % loss.data.cpu().numpy(), '| test accuracy: %.2f' % accuracy)





test_output = cnn(test_x[:10])



# !!!!!!!! Change in here !!!!!!!!! #

pred_y = torch.max(test_output, 1)[1].cuda().data # move the computation in GPU



print(pred_y, 'prediction number')

print(test_y[:10], 'real number')

 

 

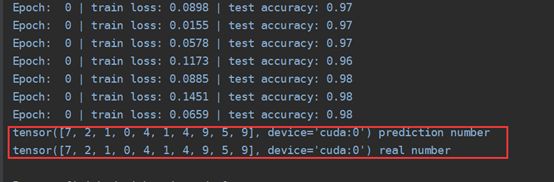
运行结果 ：

在一定轮数的训练之后  输入预测值和真实值的比较

GPU加速后 肉眼可见的训练速度加快

 

 

 

 

-------------------------------------------dropout-----------------------------------------------------------------

#############################################################################################################################################

 

torch.nn.Dropout(0.5),

每次随机抽取一定百分比的神经元 去进行传播

用训练次数来弥补可能丢失的信息

 

 

训练时需要dropout 但是测试时不需要

 

训练时需要dropout 但是测试时不需要。

所以在测试之前需要把dropout屏蔽掉，如图

 

 

完整代码：

 

import torch

import matplotlib.pyplot as plt



# torch.manual_seed(1)    # reproducible



N_SAMPLES = 20

N_HIDDEN = 300



# training data

x = torch.unsqueeze(torch.linspace(-1, 1, N_SAMPLES), 1)

y = x + 0.3*torch.normal(torch.zeros(N_SAMPLES, 1), torch.ones(N_SAMPLES, 1))



# test data

test_x = torch.unsqueeze(torch.linspace(-1, 1, N_SAMPLES), 1)

test_y = test_x + 0.3*torch.normal(torch.zeros(N_SAMPLES, 1), torch.ones(N_SAMPLES, 1))



# show data

plt.scatter(x.data.numpy(), y.data.numpy(), c='magenta', s=50, alpha=0.5, label='train')

plt.scatter(test_x.data.numpy(), test_y.data.numpy(), c='cyan', s=50, alpha=0.5, label='test')

plt.legend(loc='upper left')

plt.ylim((-2.5, 2.5))

plt.show()



net_overfitting = torch.nn.Sequential(

    torch.nn.Linear(1, N_HIDDEN),

    torch.nn.ReLU(),

    torch.nn.Linear(N_HIDDEN, N_HIDDEN),

    torch.nn.ReLU(),

    torch.nn.Linear(N_HIDDEN, 1),

)



net_dropped = torch.nn.Sequential(

    torch.nn.Linear(1, N_HIDDEN),

    torch.nn.Dropout(0.5),  # drop 50% of the neuron

    torch.nn.ReLU(),

    torch.nn.Linear(N_HIDDEN, N_HIDDEN),

    torch.nn.Dropout(0.5),  # drop 50% of the neuron

    torch.nn.ReLU(),

    torch.nn.Linear(N_HIDDEN, 1),

)



print(net_overfitting)  # net architecture

print(net_dropped)



optimizer_ofit = torch.optim.Adam(net_overfitting.parameters(), lr=0.01)

optimizer_drop = torch.optim.Adam(net_dropped.parameters(), lr=0.01)

loss_func = torch.nn.MSELoss()



plt.ion()   # something about plotting



for t in range(500):

    pred_ofit = net_overfitting(x)

    pred_drop = net_dropped(x)

    loss_ofit = loss_func(pred_ofit, y)

    loss_drop = loss_func(pred_drop, y)



    optimizer_ofit.zero_grad()

    optimizer_drop.zero_grad()

    loss_ofit.backward()

    loss_drop.backward()

    optimizer_ofit.step()

    optimizer_drop.step()



    if t % 10 == 0:

        # change to eval mode in order to fix drop out effect

        net_overfitting.eval()

        net_dropped.eval()  # parameters for dropout differ from train mode



        # plotting

        plt.cla()

        test_pred_ofit = net_overfitting(test_x)

        test_pred_drop = net_dropped(test_x)

        plt.scatter(x.data.numpy(), y.data.numpy(), c='magenta', s=50, alpha=0.3, label='train')

        plt.scatter(test_x.data.numpy(), test_y.data.numpy(), c='cyan', s=50, alpha=0.3, label='test')

        plt.plot(test_x.data.numpy(), test_pred_ofit.data.numpy(), 'r-', lw=3, label='overfitting')

        plt.plot(test_x.data.numpy(), test_pred_drop.data.numpy(), 'b--', lw=3, label='dropout(50%)')

        plt.text(0, -1.2, 'overfitting loss=%.4f' % loss_func(test_pred_ofit, test_y).data.numpy(), fontdict={'size': 20, 'color':  'red'})

        plt.text(0, -1.5, 'dropout loss=%.4f' % loss_func(test_pred_drop, test_y).data.numpy(), fontdict={'size': 20, 'color': 'blue'})

        plt.legend(loc='upper left'); plt.ylim((-2.5, 2.5));plt.pause(0.1)



        # change back to train mode

        net_overfitting.train()

        net_dropped.train()



plt.ioff()

plt.show()

 

 

运行结果：

 

 

 

----------------------------------bach normalization-----------------------------------------------------

#############################################################################################################################################

 

 

 

每一个BN  都被添加在全连接层和激活函数之间

是处理数据的一种方式  

对全连接层后输出的数据进行处理，避免数据分布在激活函数的无效区间，随着训练 神经网络会死掉

比如tanh激活函数

经过BN层处理数据以后，用BN拉回到（0,1）  这样就可以避免梯度爆炸和梯度消失

 

 

 

完整代码：

为了画图  代码不是很好理解

 

import torch

from torch import nn

from torch.nn import init

import torch.utils.data as Data

import matplotlib.pyplot as plt

import numpy as np



# torch.manual_seed(1)    # reproducible

# np.random.seed(1)



# Hyper parameters

N_SAMPLES = 2000

BATCH_SIZE = 64

EPOCH = 12

LR = 0.03

N_HIDDEN = 8

ACTIVATION = torch.tanh

B_INIT = -0.2   # use a bad bias constant initializer



# training data

x = np.linspace(-7, 10, N_SAMPLES)[:, np.newaxis]

noise = np.random.normal(0, 2, x.shape)

y = np.square(x) - 5 + noise



# test data

test_x = np.linspace(-7, 10, 200)[:, np.newaxis]

noise = np.random.normal(0, 2, test_x.shape)

test_y = np.square(test_x) - 5 + noise



train_x, train_y = torch.from_numpy(x).float(), torch.from_numpy(y).float()

test_x = torch.from_numpy(test_x).float()

test_y = torch.from_numpy(test_y).float()



train_dataset = Data.TensorDataset(train_x, train_y)

train_loader = Data.DataLoader(dataset=train_dataset, batch_size=BATCH_SIZE, shuffle=True, num_workers=2,)



# show data

plt.scatter(train_x.numpy(), train_y.numpy(), c='#FF9359', s=50, alpha=0.2, label='train')

plt.legend(loc='upper left')





class Net(nn.Module):

    def __init__(self, batch_normalization=False):

        super(Net, self).__init__()

        self.do_bn = batch_normalization

        self.fcs = []

        self.bns = []

        self.bn_input = nn.BatchNorm1d(1, momentum=0.5)   # for input data



        for i in range(N_HIDDEN):               # build hidden layers and BN layers

            input_size = 1 if i == 0 else 10

            fc = nn.Linear(input_size, 10)

            setattr(self, 'fc%i' % i, fc)       # IMPORTANT set layer to the Module

            self._set_init(fc)                  # parameters initialization

            self.fcs.append(fc)

            if self.do_bn:

                bn = nn.BatchNorm1d(10, momentum=0.5)

                setattr(self, 'bn%i' % i, bn)   # IMPORTANT set layer to the Module

                self.bns.append(bn)



        self.predict = nn.Linear(10, 1)         # output layer

        self._set_init(self.predict)            # parameters initialization



    def _set_init(self, layer):

        init.normal_(layer.weight, mean=0., std=.1)

        init.constant_(layer.bias, B_INIT)



    def forward(self, x):

        pre_activation = [x]

        if self.do_bn: x = self.bn_input(x)     # input batch normalization

        layer_input = [x]

        for i in range(N_HIDDEN):

            x = self.fcs[i](x)

            pre_activation.append(x)

            if self.do_bn: x = self.bns[i](x)   # batch normalization

            x = ACTIVATION(x)

            layer_input.append(x)

        out = self.predict(x)

        return out, layer_input, pre_activation



nets = [Net(batch_normalization=False), Net(batch_normalization=True)]



# print(*nets)    # print net architecture



opts = [torch.optim.Adam(net.parameters(), lr=LR) for net in nets]



loss_func = torch.nn.MSELoss()





def plot_histogram(l_in, l_in_bn, pre_ac, pre_ac_bn):

    for i, (ax_pa, ax_pa_bn, ax, ax_bn) in enumerate(zip(axs[0, :], axs[1, :], axs[2, :], axs[3, :])):

        [a.clear() for a in [ax_pa, ax_pa_bn, ax, ax_bn]]

        if i == 0:

            p_range = (-7, 10);the_range = (-7, 10)

        else:

            p_range = (-4, 4);the_range = (-1, 1)

        ax_pa.set_title('L' + str(i))

        ax_pa.hist(pre_ac[i].data.numpy().ravel(), bins=10, range=p_range, color='#FF9359', alpha=0.5);ax_pa_bn.hist(pre_ac_bn[i].data.numpy().ravel(), bins=10, range=p_range, color='#74BCFF', alpha=0.5)

        ax.hist(l_in[i].data.numpy().ravel(), bins=10, range=the_range, color='#FF9359');ax_bn.hist(l_in_bn[i].data.numpy().ravel(), bins=10, range=the_range, color='#74BCFF')

        for a in [ax_pa, ax, ax_pa_bn, ax_bn]: a.set_yticks(());a.set_xticks(())

        ax_pa_bn.set_xticks(p_range);ax_bn.set_xticks(the_range)

        axs[0, 0].set_ylabel('PreAct');axs[1, 0].set_ylabel('BN PreAct');axs[2, 0].set_ylabel('Act');axs[3, 0].set_ylabel('BN Act')

    plt.pause(0.01)





if __name__ == "__main__":

    f, axs = plt.subplots(4, N_HIDDEN + 1, figsize=(10, 5))

    plt.ion()  # something about plotting

    plt.show()



    # training

    losses = [[], []]  # recode loss for two networks



    for epoch in range(EPOCH):

        print('Epoch: ', epoch)

        layer_inputs, pre_acts = [], []

        for net, l in zip(nets, losses):

            net.eval()              # set eval mode to fix moving_mean and moving_var

            pred, layer_input, pre_act = net(test_x)

            l.append(loss_func(pred, test_y).data.item())

            layer_inputs.append(layer_input)

            pre_acts.append(pre_act)

            net.train()             # free moving_mean and moving_var

        plot_histogram(*layer_inputs, *pre_acts)     # plot histogram



        for step, (b_x, b_y) in enumerate(train_loader):

            for net, opt in zip(nets, opts):     # train for each network

                pred, _, _ = net(b_x)

                loss = loss_func(pred, b_y)

                opt.zero_grad()

                loss.backward()

                opt.step()    # it will also learns the parameters in Batch Normalization



    plt.ioff()



    # plot training loss

    plt.figure(2)

    plt.plot(losses[0], c='#FF9359', lw=3, label='Original')

    plt.plot(losses[1], c='#74BCFF', lw=3, label='Batch Normalization')

    plt.xlabel('step');plt.ylabel('test loss');plt.ylim((0, 2000));plt.legend(loc='best')



    # evaluation

    # set net to eval mode to freeze the parameters in batch normalization layers

    [net.eval() for net in nets]    # set eval mode to fix moving_mean and moving_var

    preds = [net(test_x)[0] for net in nets]

    plt.figure(3)

    plt.plot(test_x.data.numpy(), preds[0].data.numpy(), c='#FF9359', lw=4, label='Original')

    plt.plot(test_x.data.numpy(), preds[1].data.numpy(), c='#74BCFF', lw=4, label='Batch Normalization')

    plt.scatter(test_x.data.numpy(), test_y.data.numpy(), c='r', s=50, alpha=0.2, label='train')

    plt.legend(loc='best')

    plt.show()

 

 

运行结果：